-
1、以斜边长为2的等腰直角三角形的斜边所在直线为旋转轴,将该三角形旋转一周所得几何体的表面积为( )A、 B、 C、 D、
-
2、A、 B、 C、 D、
-
3、设全集 , 集合 , , 则( )A、{2} B、 C、 D、
-
4、如图,在中,已知 , , , 边上的中点为 , 点是边上的动点(不含端点), , 相交于点 .
 (1)、求的正弦值;(2)、当点为中点时,求的余弦值.(3)、当取得最小值时,设 , 求的值.
(1)、求的正弦值;(2)、当点为中点时,求的余弦值.(3)、当取得最小值时,设 , 求的值. -
5、已知平面四边形 , , , , , 现将沿边折起,使得平面平面 , 点为线段的中点.
 (1)、求证:平面;(2)、若为的中点,求与平面所成角的余弦值.(3)、在(2)的条件下,求平面与平面所成二面角的余弦值.
(1)、求证:平面;(2)、若为的中点,求与平面所成角的余弦值.(3)、在(2)的条件下,求平面与平面所成二面角的余弦值. -
6、已知在中,角所对的边分别为 , , , 且(1)、求角的大小;(2)、若 , 的面积为 , 求的周长.
-
7、已知向量 .(1)、若 , 求;(2)、若 , , 求与的夹角的余弦值.
-
8、已知在上的投影向量为 , 则的值为.
-
9、已知中,角A,B,C所对的边分别为a,b,c, , 则 .
-
10、如图,在正方体中,点为线段上一动点,则下列说法正确的是( )
 A、直线平面 B、异面直线与所成角的取值范围是 C、平面 D、平面与底面的交线平行于直线
A、直线平面 B、异面直线与所成角的取值范围是 C、平面 D、平面与底面的交线平行于直线 -
11、设满足 , 其面积为 , 则( )A、周长为 B、 C、外接圆的面积为 D、中线长为
-
12、已知与是共轭复数,以下4个命题一定正确的是( )A、 B、 C、 D、
-
13、在中,若动点满足 , 则点的轨迹一定经过的( )A、重心 B、垂心 C、外心 D、内心
-
14、一海轮从A处出发,以每小时40海里的速度沿南偏东的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东 , 在B处观察灯塔,其方向是北偏东 , 那么B,C两点间的距离是( )A、海里 B、海里 C、海里 D、海里
-
15、已知内角A、B、C的对边分别为a、b、c,若的面积为 , 则为( )A、 B、 C、 D、
-
16、已知是不同的直线,是不同的平面,则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
17、如图,已知 , 用表示 , 则等于
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、若复数满足 , 则的虚部为( )A、 B、 C、 D、1
-
19、如图,在直三棱柱中, .
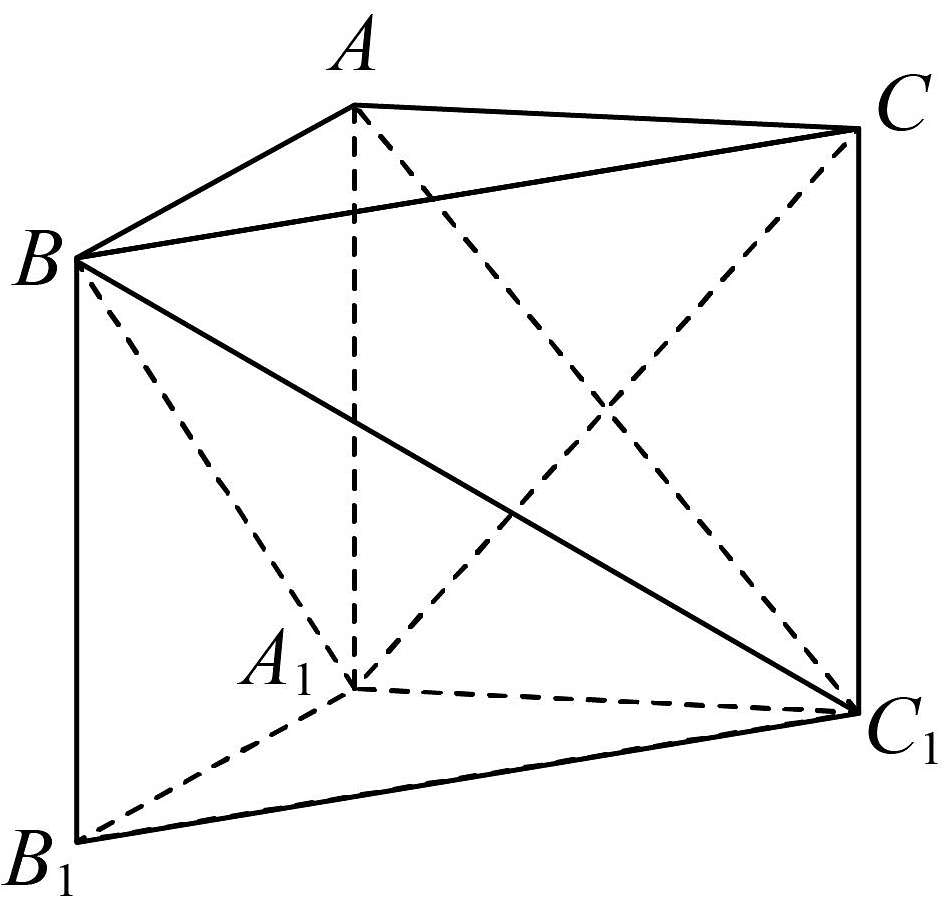 (1)、证明:平面;(2)、求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值. -
20、如图,已知在四棱锥中,平面 , 四边形为直角梯形, , , 点是棱上靠近端的三等分点,点是棱上一点.
 (1)、证明:平面;(2)、求点到平面的距离;(3)、求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、求点到平面的距离;(3)、求平面与平面夹角的余弦值.