-
1、若复数 , 则( )A、 B、 C、 D、4
-
2、已知集合 , 则( )A、 B、 C、 D、
-
3、命题“ , ”的否定是 .
-
4、已知A,B分别是双曲线的左、右顶点,点是双曲线C上的一点,直线PA,PB的斜率分别为 , , 且.(1)、求双曲线C的方程;(2)、已知过点的直线 , 交C的左,右两支于D,E两点(异于A,B).
(i)求m的取值范围;
(ii)设直线与直线交于点Q,求证:点Q在定直线上.
-
5、已知两直线和的交点为 .(1)、直线过点且与直线平行,求直线的一般式方程;(2)、圆过点且与相切于点 , 求圆的一般方程.
-
6、阿波罗尼斯是古希腊著名数学家,与阿基米德、欧几里得并称为亚历山大时期数学三巨匠,他研究发现:如果一个动点到两个定点的距离之比为常数( , 且),那么点的轨迹为圆,这就是著名的阿波罗尼斯圆.若点到 , 的距离比为 , 则点到直线:的距离的最大值是.
-
7、已知点在焦点为的抛物线上,若 , 则.
-
8、已知向量 , , 若 , 则.
-
9、3D打印是快速成型技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层打印的方式来构造物体的技术,如图所示的塔筒为3D打印的双曲线型塔筒,该塔筒是由离心率为的双曲线的一部分围绕其旋转轴逐层旋转打印得到的,已知该塔筒(数据均以外壁即塔筒外侧表面计算)的上底直径为 , 下底直径为 , 喉部(中间最细处)的直径为 , 则该塔筒的高为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、设椭圆的一个焦点与抛物线的焦点相同,离心率为 , 则此椭圆的方程为( )A、 B、 C、 D、
-
11、已知圆与圆相交于A,B两点,则两圆公共弦所在直线的方程为( )A、 B、 C、 D、
-
12、若向量 , , 则( )A、 B、 C、 D、
-
13、如图,三棱锥中, , 平面平面 , , , 为棱的中点,为棱上的点.
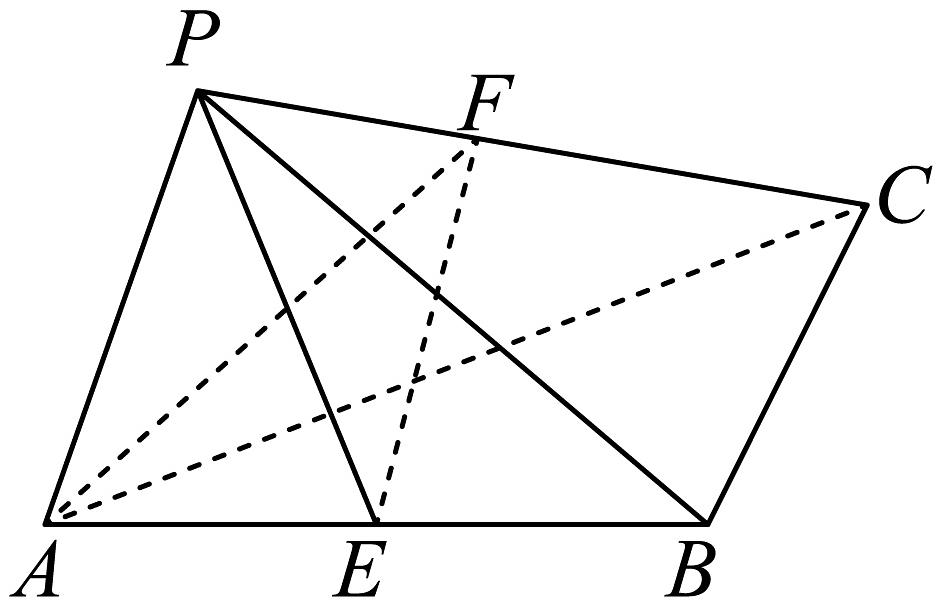 (1)、证明:平面;(2)、若二面角的正弦值为 , 求点到平面的距离.
(1)、证明:平面;(2)、若二面角的正弦值为 , 求点到平面的距离. -
14、已知函数在上单调,且 , 则的最大值为 .
-
15、已知等比数列的前项和为 , 若 , 则.
-
16、在中,已知 , , , 点是的中点,点是线段上一点,且 , 连接并延长交边于点 , 则线段的长度为( )A、 B、 C、 D、
-
17、如图,圆柱的底面直径为3,母线长为4, , 分别为该圆柱的上、下底面的直径,且 , 则三棱锥的体积是( )
 A、24 B、18 C、12 D、6
A、24 B、18 C、12 D、6 -
18、药房里有若干味药.药剂师用这些药配成22副药方,每副药方中恰有5味药,从中任选的三味药都恰好只包含在某一副药方中.(1)、药房中共有几味药?(2)、药物分为烈性药和非烈性药,要求每副药方中至少有一味是烈性药.
(i)假设药房中有7味烈性药,证明:全部药方中一定有一副药方至少含有4味烈性药;
(ii)证明:全部药方中一定有一副药方至少含有4味烈性药.
-
19、已知数列 , 满足 , 记 .(1)、求数列的通项公式;(2)、求证:;(3)、设数列的前n项和为 , 证明: .
-
20、小明参加一个抽纸牌游戏,规则如下:有九张质地完全相同的纸牌,其中有一张大王牌,其余四种花色为:红桃、黑桃、方块、梅花各2张.逐次从9张牌中不放回地随机抽取一张纸牌,每次抽牌后,都往牌堆中加入一张新的大王牌.(1)、求小明在前两次抽牌中只抽到一张大王牌的情况下,第三次抽牌抽到红桃牌的概率.(2)、抽牌过程中,若抽到大王牌,则宣告游戏结束:若累计抽到两张花色相同的纸牌,也宣告游戏结束;否则游戏继续.用X表示小明在游戏中一共抽到的纸牌数,求X的分布列.