-
1、已知 , , , 则.
-
2、已知函数为奇函数,则实数的值为.
-
3、已知函数 , 则下列结论正确的是( )A、的图象关于轴对称 B、的图象关于点对称 C、的图象关于直线对称 D、是的极大值点
-
4、已知 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则的最大值为 D、 , , 使得
-
5、如果关于的不等式的解集为 , 那么下列数值中,可取到的数为( )A、 B、0 C、1 D、2
-
6、已知直线是函数图象的任意两条对称轴,且的最小值为 , 则的单调递增区间是( )A、 B、 C、 D、
-
7、已知(且)是上的奇函数,且(1)、求的解析式;(2)、把区间等分成份,记等分点的横坐标依次为 , , 记 , 是否存在正整数n,使不等式有解?若存在,求出所有n的值,若不存在,说明理由;(3)、函数在区间上的值域是 , 求的取值范围.
-
8、已知 , 且 , 则( )A、 B、 C、 D、
-
9、如图,在四棱锥中,底面是正方形,侧棱底面 , , 是的中点,作交于点 .
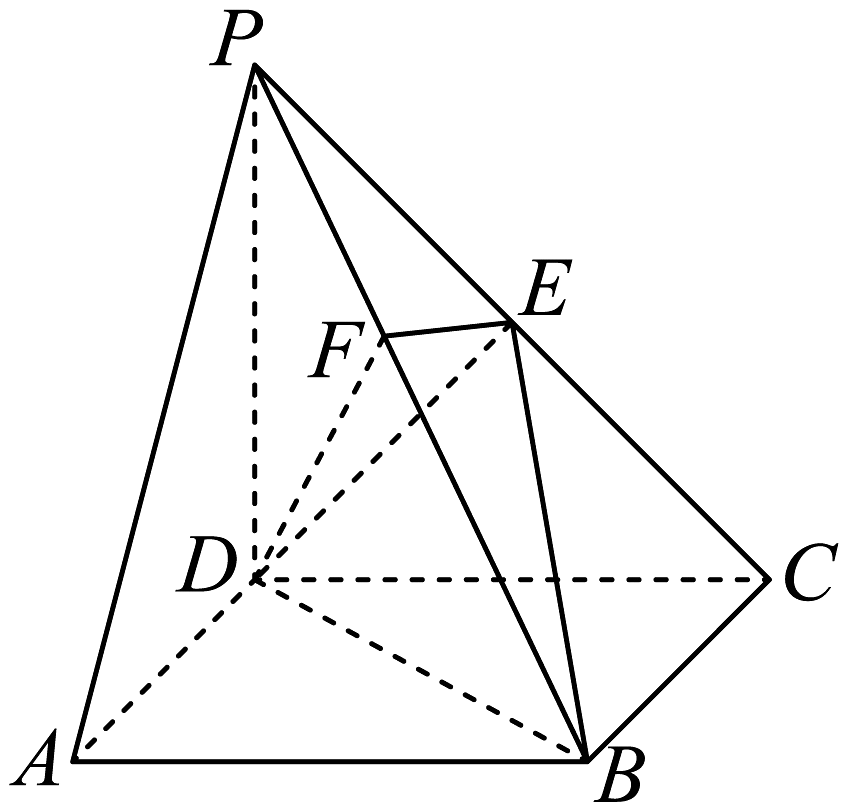 (1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离.
(1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离. -
10、若 , , , 则以下不等式正确的是( )A、 B、 C、 D、
-
11、已知函数 , .若的零点恰为的零点,则a的最大值是.
-
12、已知抛物线的焦点为F,斜率为1的直线l过F与C交于A,B两点,AB的中点到抛物线准线的距离为8,则 .
-
13、已知平面向量 , , 则( )A、当时, B、若 , 则 C、若 , 则 D、若与的夹角为钝角,则
-
14、在斜三角形中,角的对边分别为 , 点满足 , 且 , 则的面积为( )A、 B、 C、 D、
-
15、解二元一次方程组是数学学习的必备技能.设有满足条件的二元一次方程组.(1)、用消元法解此方程组,直接写出该方程组的两个解;(2)、通过求解,不难发现两个解的分母是由方程组中的系数所唯一确定的一个数,按照它们在方程组中的位置,把它们排成一个数表 , 由此可以看出是这个数表中左上到右下对角线上两个数的乘积减去右上到左下对角线上两个数的乘积的差,称为该数表的二阶行列式,记为.当≠0时,二元一次方程组有唯一一组解.同样的,行列式称为三阶行列式,且=.
(i)用二阶行列式表示方程组的两个解;
(ii)对于三元一次方程组 , 类比二阶行列式,用三阶行列式推导使得该三元一次方程组有唯一一组解的条件(结论不得使用行列式表达),并用三阶行列式表示该方程组的解.
(3)、若存在 , 使得 , 求的取值范围. -
16、已知函数 ,(1)、当时,恒成立,求a的取值范围;(2)、设 , 为上不同的两点 , 设AB两点所在直线的斜率为K,证明:
-
17、已知函数 .(1)、若在上存在极小值,求实数的取值范围(2)、讨论在上的零点个数.
-
18、已知函数的部分图象如图所示.该图象与轴交于点 , 与轴交于两点, 为图象的最高点,且的面积为 .
 (1)、求的解析式及其单调递增区间.(2)、若将的图象向右平移个单位长度,再将所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数的图象.若 , 求的值.
(1)、求的解析式及其单调递增区间.(2)、若将的图象向右平移个单位长度,再将所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数的图象.若 , 求的值. -
19、已知函数 , , 若 , , 则的最小值为 .
-
20、已知x1、x2分别是函数f(x)=ex+x-4、g(x)=lnx+x-4的零点,则的值为( )A、 B、 C、3 D、4