-
1、如图,在直三棱柱中,D为棱的中点, , , , 则异面直线CD与所成角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,在直三棱柱中,为直角,侧面为正方形, , , 分别为 , 的中点.
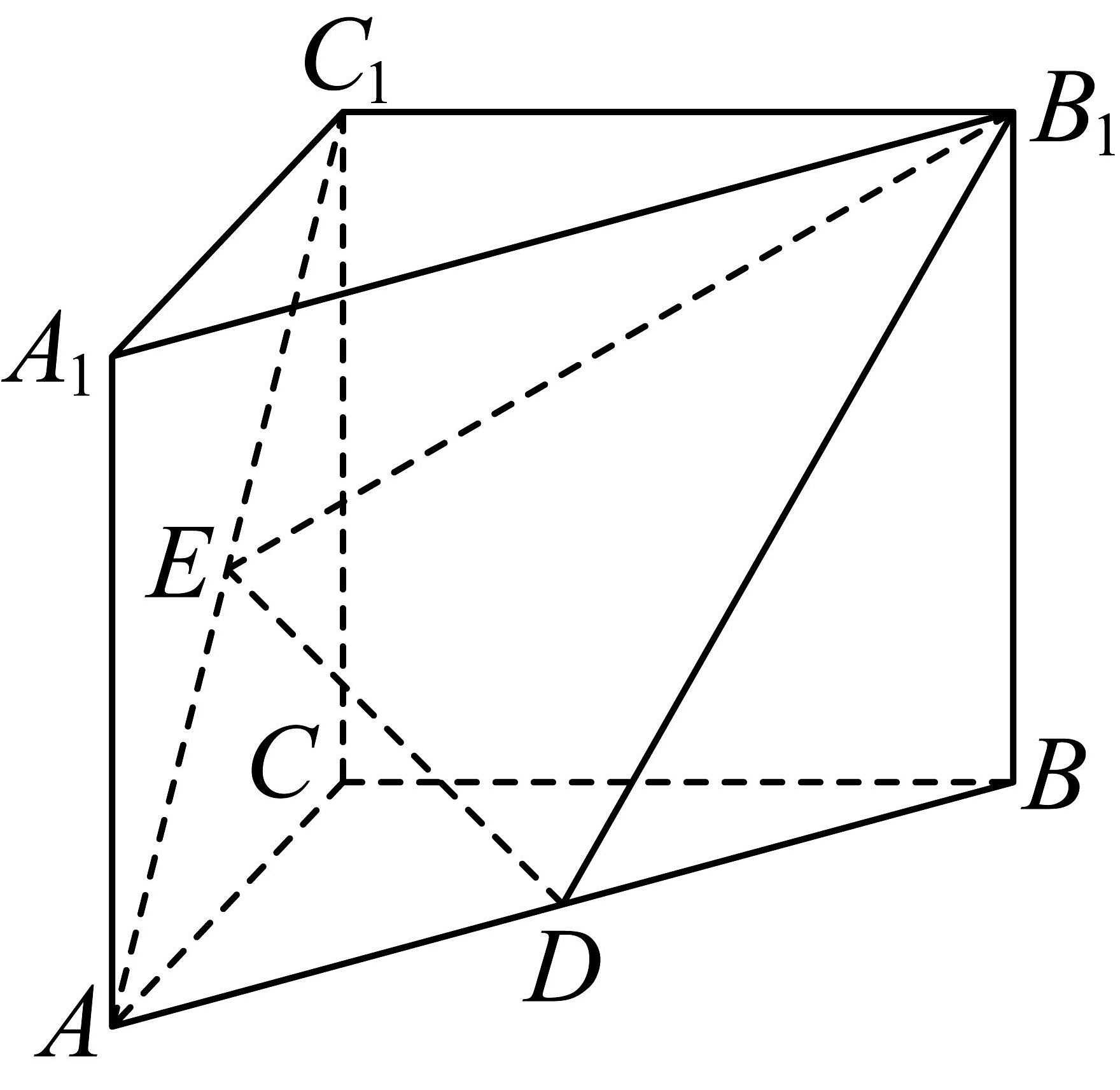 (1)、求证:平面;(2)、求直线与平面所成角的正弦值.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值. -
3、某场知识竞赛比赛中,甲、乙、丙三个家庭同时回答一道有关环保知识的问题.已知甲家庭回答正确这道题的概率是 , 甲、丙两个家庭都回答错误的概率是 , 乙、丙两个家庭都回答正确的概率是 , 若各家庭回答是否正确互不影响.(1)、求乙、丙两个家庭各自回答正确这道题的概率;(2)、求甲、乙、丙三个家庭中不少于2个家庭回答正确这道题的概率.
-
4、小欣和小敏打算利用节假日在内江游玩,其中4个景点分别是:“张大千纪念馆”、“重龙山”、“罗泉古镇”和“古宇湖”.他们各自在这4个景点中任意选择一个游览,每个被选择的可能性相同.(1)、小欣选择“罗泉古镇”的概率是多少?(2)、用画树状图或列表的方法,求小欣和小敏恰好选择同一景点的概率.
-
5、如图,在正方体中,在上,且 , 在对角线上,且.若 , , .
 (1)、用 , , 表示;(2)、用 , , 表示.
(1)、用 , , 表示;(2)、用 , , 表示. -
6、在如图所示的试验装置中,两个正方形框架 , 的边长都是1,且它们所在的平面互相垂直.活动弹子 , 分别在正方形对角线和上移动,且和的长度保持相等,记 , 则当时,的长最小.

-
7、如图所示,电路原件 , , 正常工作的概率分别为 , , , 则电路能正常工作的概率为 .

-
8、如图,在棱长为1的正方体中,为面的中心,、分别为和的中点,则( )
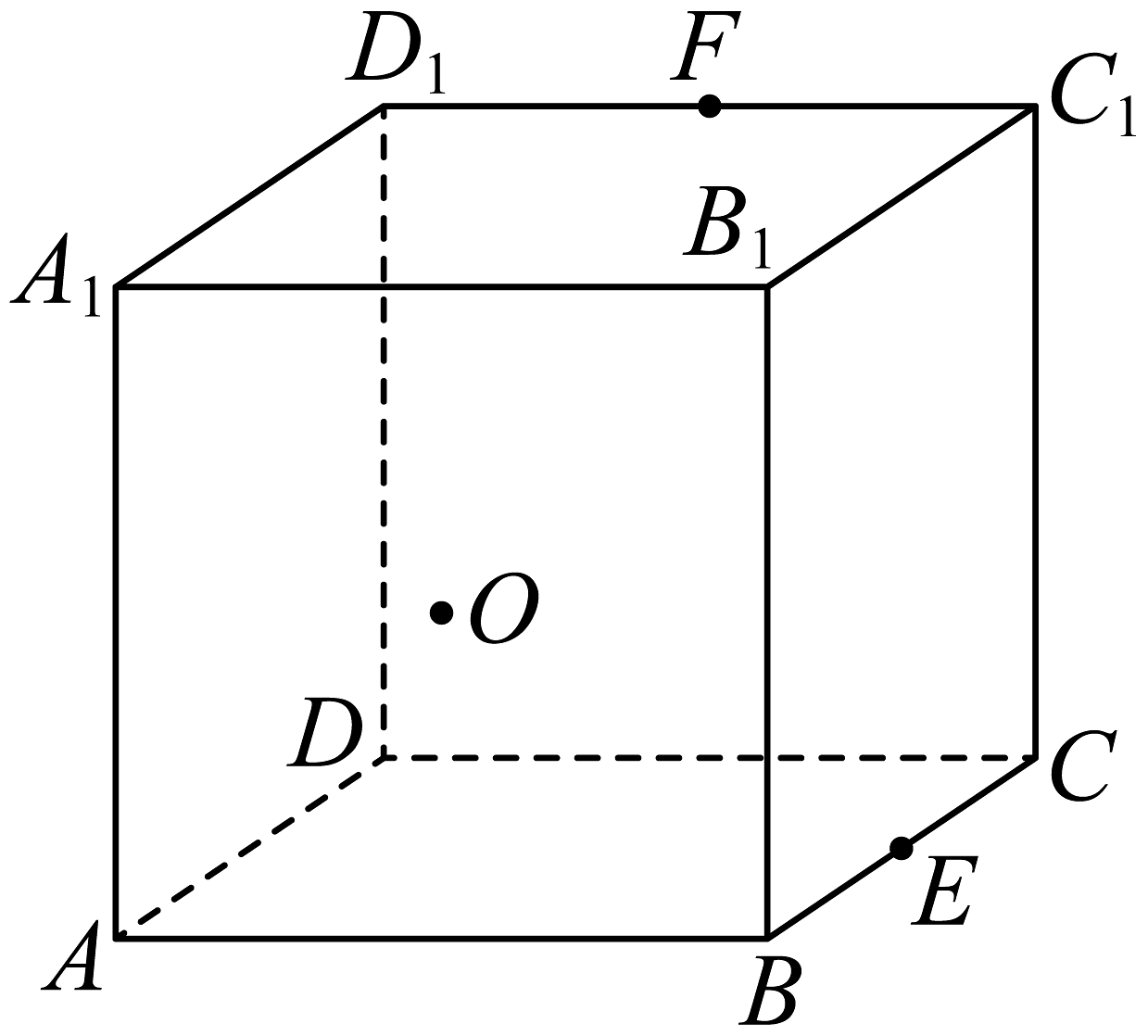 A、平面 B、平面与平面相交 C、点到直线的距离为 D、点到平面的距离为
A、平面 B、平面与平面相交 C、点到直线的距离为 D、点到平面的距离为 -
9、已知 , , 则下列说法中正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果互斥,那么 D、如果互斥,那么
-
10、已知事件与互斥,它们都不发生的概率为 , 且 , 则( ).A、 B、 C、 D、
-
11、设 , 向量 , 且 , 则等于( )A、2 B、 C、3 D、4
-
12、为空间的一个基底,且存在实数 , , 使得 , 则 , , 的值分别为( )A、 , , B、 , , C、 , , D、 , ,
-
13、设 , 为两个随机事件,给出以下命题,不正确的是( )A、若 , , , 则 , 为相互独立事件 B、若 , , , 则 , 为相互独立事件 C、若 , , , 则 , 为相互独立事件 D、若 , , , 则 , 为相互独立事件
-
14、若直线的方向向量为 , , , 平面的法向量为 , 6, , 则( )A、 B、 C、 D、与位置关系不确定
-
15、已知 , 是空间两个不共线的向量, , 那么必有( )A、 , 共线 B、 , 共线 C、 , , 共面 D、 , , 不共面
-
16、掷一枚骰子,设事件出现的点数不小于5 , 出现的点数为偶数 , 则事件A与事件B的关系是( )A、 B、出现的点数为6 C、事件A与B互斥 D、事件A与B是对立事件
-
17、已知a,b,c分别是三内角A,B,C所对的三边,且 .(1)、求A的大小;(2)、若 , 的面积为 , 求a,b;(3)、求的取值范围.
-
18、已知向量 , 且 , 则 .
-
19、已知圆: , 则圆心的坐标和半径分别为( )A、 , B、 , C、 , D、 ,
-
20、已知等比数列中,且是和的等差中项.(1)、求数列的通项公式;(2)、若函数 , 满足 , 求的前n项和.