-
1、“”是“直线与圆相切”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
2、已知平面向量为单位向量,若 , 则( )A、0 B、1 C、 D、3
-
3、若复数满足 , 则复数( )A、 B、 C、 D、
-
4、有一组数据,按从小到大排列为: , 这组数据的分位数等于他们的平均数,则为( )A、12 B、11 C、10 D、9
-
5、直线的倾斜角是( )A、 B、 C、 D、
-
6、定义符号函数为 , 已知 , 令 , .(1)、若函数在区间上单调,求实数的取值范围;(2)、当时,若函数与的图象有且仅有一个交点,求实数的取值范围;(3)、若 , , 使得成立,求实数的取值范围.
-
7、已知函数是定义域为的奇函数,当时,.(1)、求实数的值;(2)、判断在区间上的单调性,并用定义法证明;(3)、若 , 求实数的取值范围.
-
8、已知正实数x,y满足.(1)、求的最大值;(2)、若不等式有解,求实数的取值范围.
-
9、已知集合 , .(1)、当时,求 , ;(2)、若 , 求实数的取值范围.
-
10、已知 , 则.
-
11、下列说法中正确的是( )A、与表示同一个函数 B、为偶函数,且在区间上单调递增 C、既是奇函数,又是偶函数 D、若函数的定义域为 , 则函数的定义域为
-
12、已知 , 且 , 则下列结论中正确的是( )A、 B、 C、 D、
-
13、已知函数 , 若在区间上既有最大值,又有最小值,则的最大值为( )A、1 B、2 C、3 D、4
-
14、已知函数的定义域为 , 且对 , , 则( )A、 B、 C、 D、2
-
15、已知实数 , 且“”的一个必要不充分条件是“”,则实数的取值范围是( )A、 B、 C、 D、
-
16、已知偶函数在区间上单调递增且存在最大值为 , 则函数在区间上( )A、单调递增且最大值为 B、单调递增且最小值为 C、单调递减且最大值为 D、单调递减且最小值为
-
17、函数的图象大致是( )A、
 B、
B、 C、
C、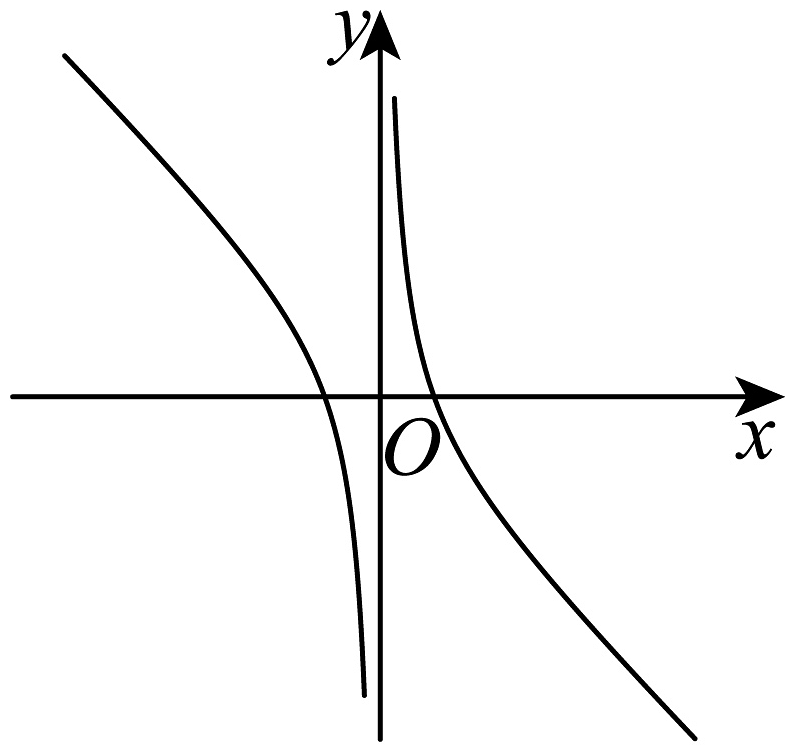 D、
D、
-
18、命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,
-
19、已知集合 , 则( )A、 B、 C、 D、
-
20、已知空间中三点 , 则下列说法正确的是( )A、 B、与是共线向量 C、和夹角的余弦值是1 D、与同向的单位向量是