版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，过 $F_{1}$ 的直线交椭圆 $C$ 于 $A$ 、 $B$ 两点，其中 $B$ 为上顶点，且 $3 \vec{A F_{1}} = 2 \vec{F_{1} B}$ ，则椭圆 $C$ 的离心率 $e =$ （）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{2}}{5}$ D、 $\frac{\sqrt{10}}{5}$

查看解析
2、已知平面上两定点 $A, B$ ，则满足 $\frac{|P A|}{|P B|} = k$ （常数 $k > 0$ 且 $k \neq 1$ ）的动点 $P$ 的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆.已知在 $△ P A B$ 中， $|A B| = 4$ ， $|P A| = 2 |P B|$ ，则 $△ P A B$ 面积的最大值是（）

A、4 B、 $\frac{8}{3}$ C、 $\frac{32}{3}$ D、 $\frac{16}{3}$

查看解析
3、已知椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$ 的下焦点是 $F_{1}$ ，上焦点是 $F_{2}$ ，点 $P$ 在椭圆上，如果线段 $P F_{1}$ 的中点在 $x$ 轴上，那么 $|P F_{2}| : |P F_{1}| =$ （）

A、 $2 : 7$ B、 $1 : 7$ C、 $1 : 2$ D、 $3 : 4$

查看解析
4、若直线 $a x + (a - 3) y + 3 = 0$ 与直线 $x + a y - 3 = 0$ 垂直，则 $a$ 的值是（）

A、2 B、0 C、0或2 D、2或 $- 2$

查看解析
5、若点 $P (1, m)$ 在圆 $C : x^{2} + y^{2} - 2 x + 2 y + 1 = 0$ 内，则 $m$ 的取值范围是（）

A、 $(- \infty, - 2)$ B、 $[- 2, 0]$ C、 $(0, 2)$ D、 $(- 2, 0)$

查看解析
6、向量 $\vec{a} = (x, 1, 2)$ ， $\vec{b} = (1, - y, 8)$ ，若 $\vec{a} ∥ \vec{b}$ ，则（）

A、 $x = - \frac{1}{4}$ ， $y = \frac{1}{4}$ B、 $x = \frac{1}{4}$ ， $y = - 4$ C、 $x = \frac{1}{4}$ ， $y = 4$ D、 $x = - \frac{1}{4}$ ， $y = - 4$

查看解析
7、直线l： $\sqrt{3}$ x+y﹣3＝0的倾斜角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看解析
8、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右焦点分别为 $F_{1}, F_{2}$ ，离心率为 $\frac{\sqrt{2}}{2}$ ，设 $P (x_{0}, y_{0})$ 是第一象限内椭圆 $C$ 上的一点， $P F_{1} ､ P F_{2}$ 的延长线分别交椭圆 $C$ 于点 $A, B$ ，连接 $O P, A B, A F_{2}$ ，若 $△ A P F_{2}$ 的周长为 $4 \sqrt{2}$ .

(1)、求椭圆 $C$ 的方程；

(2)、当 $P F_{2} ⊥ x$ 轴，求 $△ P A F_{2}$ 的面积；

(3)、若分别记 $O P, A B$ 的斜率分别为 $k_{1}, k_{2}$ ，求 $\frac{1}{k_{2}} - \frac{1}{k_{1}}$ 的最大值.

查看解析
9、如图所示，已知四棱锥 $P - A B C D, △ P A D$ 是以 $A D$ 为斜边的等腰直角三角形，底面 $A B C D$ 是等腰梯形，且 $B C$ $∥$ $A D, A D = 2 D C = 2 C B, ∠ A D C = 60^{\circ}, P C = \sqrt{2} B C, E$ 是 $P D$ 的中点.

(1)、求证： $C E$ $∥$ 平面 $A P B$ ；

(2)、若 $A D = 2$ ，求四棱锥 $P - A B C D$ 的体积；

(3)、求二面角 $B - P C - D$ 的平面角的余弦值.

查看解析
10、在平面直角坐标系 $x O y$ 中，已知圆 $C$ 与 $y$ 轴相切，且过点 $M (1, \sqrt{3}), N (1, - \sqrt{3})$

(1)、求圆 $C$ 的方程；

(2)、过点 $A (- 2, 0)$ 作直线 $l$ 交圆 $C$ 于 $M, N$ 两点，若 $\frac{1}{| A M |^{2}} + \frac{1}{| A N |^{2}} = \frac{17}{90}$ ，求直线 $l$ 的方程.

查看解析
11、在 $△ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，若 $b sin B - c sin C = (b - a) sin A$

(1)、求 $C$ 的大小；

(2)、若 $D$ 是线段 $A B$ 上一点，且 $A D = 2 B D, C D = 2$ ，求 $S_{△ A B C}$ 的最大值.

查看解析
12、杭州市某学校组织学生参加线上环保知识竞赛活动，现从中抽取200名学生，记录他们的首轮竞赛成绩并作出如图所示的频率直方图，根据图形，请解决下列问题：

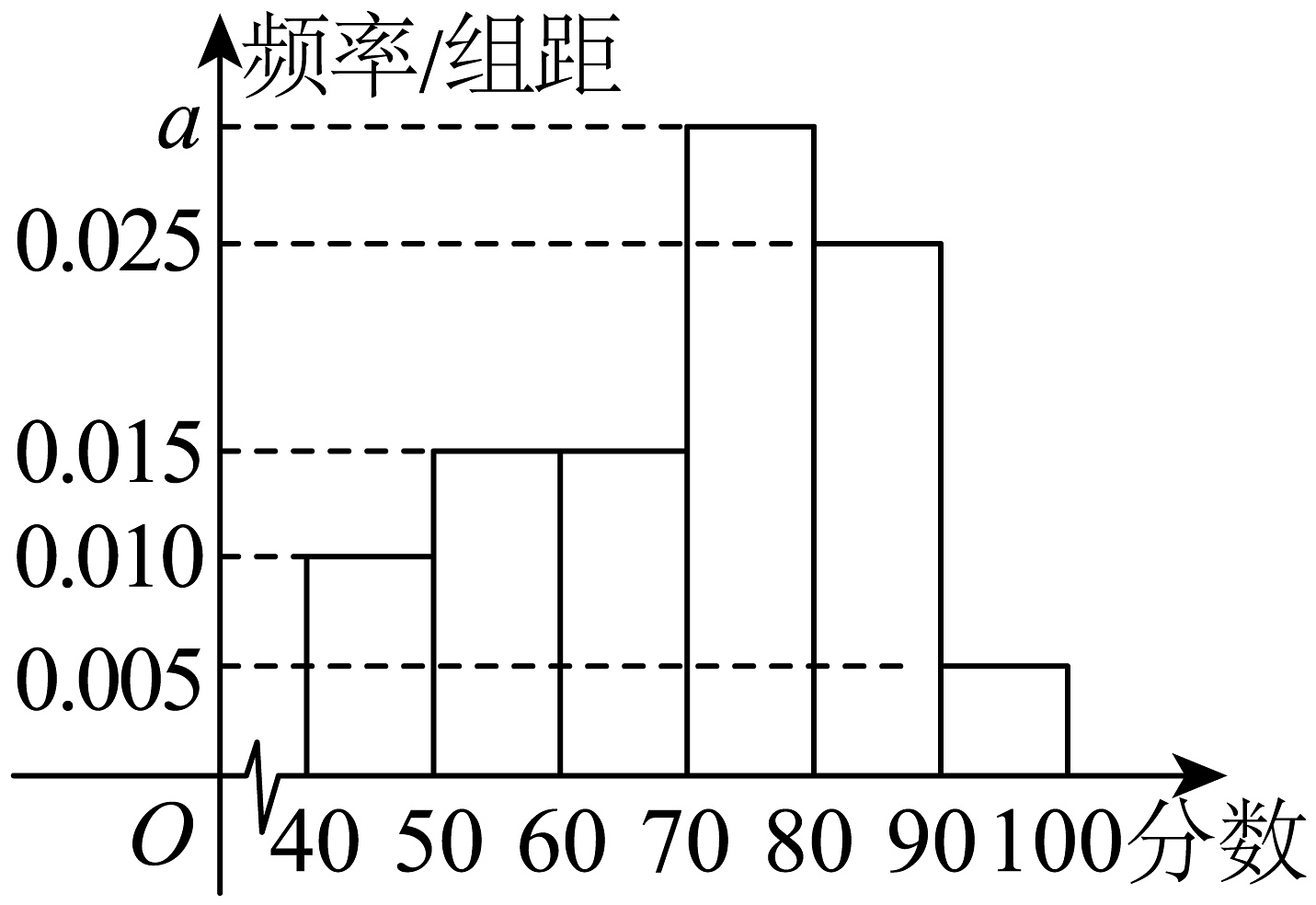(1)、若从成绩不高于60分的同学中按分层抽样方法抽取5人成绩，求5人中成绩不高于50分的人数：

(2)、已知落在 $[60, 70)$ 成绩的平均值为66，方差是7；落在 $[70, 80)$ 成绩的平均值为75，方差是4，求两组成绩的总平均数 $\bar{z}$ 和总方差 $s^{2}$ ；

(3)、若该学校安排甲､乙两位同学参加第二轮的复赛，已知甲复赛获优秀等级的概率为 $\frac{2}{3}$ ，乙复赛获优秀等级的概率为 $\frac{4}{5}$ ，甲､乙是否获优秀等级互不影响，求至少有一位同学复赛获优秀等级的概率.

查看解析
13、已知正三棱锥 $A - B C D$ 的外接球为球 $O, A B = 6, B C = 3 \sqrt{3}, P$ 是球 $O$ 上任意一点， $E$ 为 $B D$ 的中点，则 $P E$ 的取值范围为.

查看解析
14、已知椭圆 $E : \frac{x^{2}}{64} + \frac{y^{2}}{b^{2}} = 1 (0 < b < 8)$ 的左､右焦点到直线 $l : x - y - 4 = 0$ 的距离之和为 $4 \sqrt{2}$ ，则 $E$ 离心率取值范围是.

查看解析
15、已知某圆台上下底面半径分别为2和5，母线长为5，则该圆台的体积是.

查看解析
16、已知曲线 $C$ 的方程 $x^{2} + y^{2} + a |x| y = 1$ ，则以下结论正确的是（）

A、无论实数 $a$ 取何值，曲线 $C$ 都关于 $y$ 轴成轴对称 B、无论实数 $a$ 取何值，曲线 $C$ 都是封闭图形 C、当 $a = - 1$ 时，曲线 $C$ 恰好经过 $6$ 个整点（即横､纵坐标均为整数的点） D、当 $a = - 1$ 时，曲线 $C$ 所围成的区域的面积小于 $3$

查看解析
17、如图，已知正方体 $A B C D - A^{'} B^{'} C^{'} D^{'}, E, F$ 分别是上底面 $A^{'} C^{'}$ 和侧面 $C D^{'}$ 的中心，判断下列结论正确的是（）

A、存在 $x$ 使得 $\vec{A C^{'}} = x (\vec{A B} + \vec{B C} + \vec{C C^{'}})$ B、任意 $x, y$ ，使得 $\vec{A E} = \vec{A A^{'}} + x \vec{A B} + y \vec{A D}$ C、存在 $x, y$ ，使得 $\vec{A F}, \vec{A D}, x \vec{A C^{'}} + y \vec{A C}$ 共面 D、任意 $x, y$ ，使得 $\vec{A F}, \vec{A D}, x \vec{A B^{'}} + y \vec{A C^{'}}$ 共面

查看解析
18、已知直线 $l : (a + 1) x + (1 - a) y - 2 = 0$ 与动圆 $C : x^{2} + y^{2} + 2 b x + 4 b y + 5 b^{2} - 9 = 0$ ，下列说法正确的是（）

A、直线 $l$ 过定点 $(1, 2)$ B、当 $a = 1$ 时，若直线 $l$ 与圆 $C$ 相切，则 $b = 4$ C、若直线 $l$ 与圆 $C$ 相交截得弦长为定值 $d$ ，则 $d = \frac{4 \sqrt{55}}{5}$ D、当 $b = 0$ 时，直线 $l$ 截圆 $C$ 的最短弦长为 $\sqrt{7}$

查看解析
19、设 $A, B$ 是一个随机试验中的两个事件，记 $\bar{A}, \bar{B}$ 为事件 $A, B$ 的对立事件，且 $P (A) = \frac{2}{5}, P (B) = \frac{1}{3}, P (A \bar{B}) = \frac{2}{15}$ ，则 $P (\bar{A} + B) =$ （）

A、 $\frac{11}{15}$ B、 $\frac{8}{15}$ C、 $\frac{14}{15}$ D、 $\frac{13}{15}$

查看解析
20、已知直线 $l$ 经过点 $A (2, 3, 1)$ ，且 $\vec{n} = (1, 2, 1)$ 是 $l$ 的方向向量，则点 $P (4, 3, 2)$ 到 $l$ 的距离为（）

A、 $\frac{\sqrt{6}}{2}$ B、 $\frac{7}{2}$ C、 $\frac{\sqrt{14}}{2}$ D、 $\sqrt{14}$

查看解析

上一页 631 632 633 634 635 下一页跳转