-
1、FISS足球世界杯是很受全球高中生欢迎的足球赛事,中国成功获得国际中体联足球世界杯2024,2026,2028年主办权,经过大连市的积极申办,教育部正式推荐,大连最终成为2024年国际中体联足球世界杯承办地.筹备期间组委会委托A工厂生产某种纪念品,生产该纪念品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为万元,在年产量不足9万件时,(万元),在年产量不小于9万件时,(万元),每件纪念品售价为10元,通过市场分析,此纪念品当年能全部售完.(1)、写出年利润(万元)关于年产量x(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)(2)、年产量为多少万件时,该工厂在这一纪念品的生产中所获利润最大?最大利润是多少?
-
2、已知集合 , .(1)、当时,求;(2)、若 , 求实数m的取值范围.
-
3、已知函数 .(1)、证明:的奇偶性;(2)、证明:在区间上的单调性,并求在区间上的值域.
-
4、函数在上的最大值与最小值的和为2024,则.
-
5、若函数是定义在上的偶函数,则 .
-
6、已知关于的不等式的解集为 , 则下列说法正确的是( )A、 B、不等式的解集为 C、 D、不等式的解集为
-
7、中国古代重要的数学著作孙子算经下卷有题:今有物,不知其数三三数之,剩二;五五数之,剩三;七七数之,剩二问:物几何?现有如下表示:已知 , , , 若 , 则下列选项中符合题意的整数为A、 B、 C、 D、
-
8、若 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
9、已知 , 则( )A、2 B、3 C、4 D、5
-
10、下列结论正确的是A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
11、 的否定是( )A、 B、 C、 D、
-
12、已知为坐标原点,.若动点满足 , 则正数的最大值为( )A、 B、 C、 D、
-
13、在平行四边形中, , , , 是的中点,沿将翻折至的位置,使得平面平面 , 为的中点,则异面直线与所成角的余弦值为( )
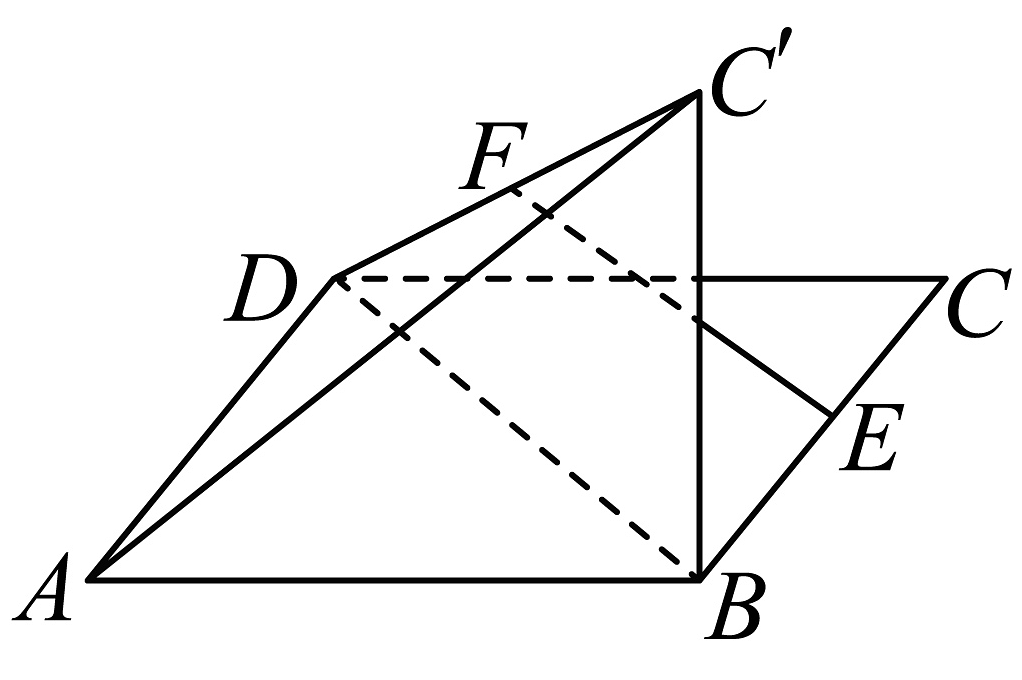 A、 B、 C、 D、
A、 B、 C、 D、 -
14、飞行棋是大家熟悉的棋类游戏,玩家通过投掷骰子来决定飞机起飞与飞行的步数.当且仅当玩家投掷出点时,飞机才能起飞.并且掷得点的游戏者可以连续投掷骰子,直至显示点数不是点.飞机起飞后,飞行步数即骰子向上的点数.(1)、求甲玩家第一轮投掷中,投郑次数的均值)(2)、对于两个离散型随机变量、 , 我们将其可能出现的结果作为一个有序数对,类似于离散型随机变量的分布列,我们可以用如下表格来表示这个有序数对的概率分布:
(记 , )
若已知 , 则事件的条件概率为.可以发现依然是一个随机变量,可以对其求期望.
(ⅰ)上述期望依旧是一个随机变量(取值不同时,期望也不同),不妨记为 , 求;
(ⅱ)若修改游戏规则,需连续掷出两次点飞机才能起飞,记表示“甲第一次未能掷出6点”,表示“甲第一次掷出点且第二次未能掷出点”,表示“甲第一次第二次均掷出点”,为甲首次使得飞机起飞时抛掷骰子的次数,求.
-
15、命题“”的否定是.
-
16、下列命题正确的有( )A、已知函数在上可导,若 , 则 B、已知函数 , 若 , 则 C、 D、设函数的导函数为 , 且 , 则
-
17、在中, , 为外心,且 , 则的最大值为( )A、 B、 C、 D、
-
18、已知函数是定义域为R的偶函数,且对任意 , , , 当时总有 , 则满足的的范围是( )A、 B、 C、 D、
-
19、在如图所示的试验装置中,两个正方形框架 , 的边长都是1,且它们所在平面互相垂直,活动弹子分别在正方形对角线和上移动,且和的长度保持相等,记 , 活动弹子在上移动.
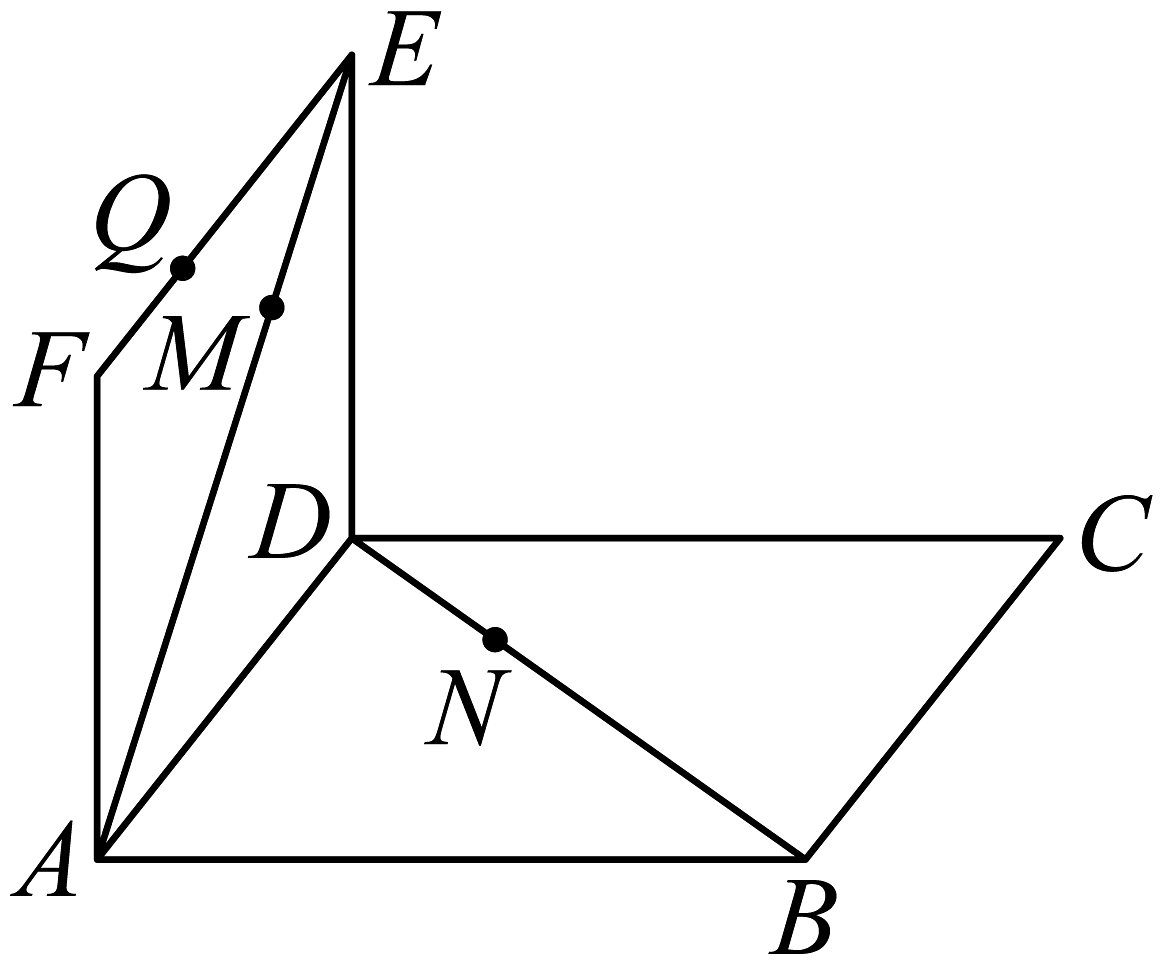 (1)、求证:直线平面;(2)、为上的点,求与平面所成角的正弦值的最大值.
(1)、求证:直线平面;(2)、为上的点,求与平面所成角的正弦值的最大值. -
20、质量监督局检测某种产品的三个质量指标 , 用综合指标核定该产品的等级.若 , 则核定该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标()
产品编号
质量指标()
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件为“在取出的2件产品中,每件产品的综合指标均满足”,求事件的概率.