版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、设 $F$ 为抛物线 $C : y^{2} = 4 x$ 的焦点，直线 $l : 2 x - a y + 2 b = 0 (a \neq 0)$ 与 $C$ 的准线 $l_{1}$ ，交于点 $A$ ．已知 $l$ 与 $C$ 相切，切点为 $B$ ，直线 $B F$ 与 $C$ 的一个交点为 $D$ ，则（）

A、点 $(a, b)$ 在 $C$ 上 B、 $∠ B A F < ∠ A F B$ C、以 $B F$ 为直径的圆与 $l_{1}$ 相离 D、直线 $A D$ 与 $C$ 相切

查看解析
2、在直角梯形 $A B C D$ ， $A B ⊥ A D$ ， $D C // A B$ ， $A D = D C =1$ ， $A B =2$ ， $E$ ， $F$ 分别为 $A B$ ， $B C$ 的中点，点 $P$ 在以A为圆心， $A D$ 为半径的圆弧 $D E M$ 上变动（如图所示），若 $\vec{A P} = λ \vec{E D} + μ \vec{A F}$ ，其中 $λ, μ ∈R$ ，则 $2 λ − μ$ 的取值范围是（）

A、 $[− \sqrt{2},1]$ B、 $[− \sqrt{2}, \sqrt{2}]$ C、 $[− \frac{1}{2}, \frac{1}{2}]$ D、 $[− \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}]$

查看解析
3、已知直线 $l : y = 2 x + b$ 与圆 $C : {(x + 2)}^{2} + {(y - 3)}^{2} = 5$ 有公共点，则b的取值范围为（）

A、 $[2, 12]$ B、 $(- \infty, 2] \cup [12, + \infty)$ C、 $[- 4, 6]$ D、 $(- \infty, - 4] \cup [6, + \infty)$

查看解析
4、为了了解高中学生课后自主学习数学时间（x分钟/每天）和他们的数学成绩（y分）的关系，某实验小组做了调查，得到一些数据（表一）.
编号
1
2
3
4
5
学习时间x
30
40
50
60
70
数学成绩y
65
78
85
99
108

(1)、求数学成绩 $y$ 与学习时间 $x$ 的相关系数（精确到0.001）；

(2)、请用相关系数说明该组数据中 $y$ 与 $x$ 之间的关系可用线性回归模型进行拟合，并求出 $y$ 关于 $x$ 的回归直线方程，并由此预测每天课后自主学习数学时间为100分钟时的数学成绩（参考数据： $\sum_{i = 1}^{5} x_{i} y_{i} = 22820, \sum_{i = 1}^{5} y_{i} = 435, \sum_{i = 1}^{5} y_{i}^{2} = 38999, {107.4}^{2} \approx 11540$ ， $x_{i}$ 的方差为200）；

(3)、基于上述调查，某校提倡学生周末在校自主学习.经过一学期的实施后，抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计，得到 $2 \times 2$ 列联表（表二）.依据表中数据及小概率值 $α = 0.001$ 的独立性检验，分析“周末在校自主学习与成绩进步”是否有关.
没有进步
有进步
合计
参与周末在校自主学习
35
130
165
未参与周末不在校自主学习
25
30
55
合计
60
160
220
附：方差： $S^{2} = \frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}$ 相关系数： $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$
回归方程 $\hat{y} = b x + a$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ， $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .
$α$
0.10
0.05
0.010
0.005
0.001
$χ_{α}$
2.706
3.841
6.635
7.879
10.828

查看解析
5、已知 $f (x) = \sqrt{3} sin ω x cos ω x - {cos}^{2} ω x (ω > 0)$ 的最小正周期为 $π$ ，

(1)、求 $f (\frac{2 π}{3})$ 的值；

(2)、若 $g (x) = f (x) + \frac{1}{2}$ 在 $(0, m)$ 上恰有 $2$ 个极值点和 $2$ 个零点，求实数 $m$ 的取值范围．

查看解析
6、已知四棱锥 $S - A B C D$ ， $S A$ ⊥面 $A B C D$ ，底面 $A B C D$ 为正方形， $S A = A B$ ， $E$ 为 $S D$ 的中点．

(1)、求证： $A E ⊥$ 面 $S C D$ ；

(2)、求直线 $B S$ 与面 $S C D$ 所成的角．

查看解析
7、在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $a + b + c = 8$

(1)、若 $b = 2, c = 3$ ，求 $cos A$ 的值；

(2)、若 $sin C + sin B = 3 sin A$ ，且 $△ A B C$ 的面积为 $S = \frac{9}{2} sin A$ ，求 $b$ 和 $c$ 的值．

查看解析
8、已知在三棱锥 $A - B C D$ 中， $A B ⊥ B D, A C ⊥ C D, A B = 8, B D = 6$ ，点 $P$ 为三棱锥 $A - B C D$ 外接球上一点，则三棱锥 $P - A B D$ 的体积最大为．

查看解析
9、一位射击运动员向一个目标射击二次，记事件 $A_{i} =$ “第 $i$ 次命中目标” $(i = 1, 2), P (A_{1}) = \frac{1}{4}$ ， $P (A_{i + 1} ∣ A_{i}) = 2 P (A_{i}), P (A_{i + 1} ∣ \bar{A_{i}}) = \frac{1}{4} (i = 1)$ ，则 $P (A_{2}) =$ ．

查看解析
10、已知正方形ABCD的边长为2，若将正方形ABCD沿对角线BD折叠成三棱锥 $A - B C D$ 则在折叠过程中，不可能出现（）

A、 $A B ⊥ C D$ B、 $A C ⊥ B D$ C、三棱锥 $A - B C D$ 的体积为 $\frac{\sqrt{2}}{3}$ D、平面 $A B D ⊥$ 平面BCD

查看解析
11、已知 $sin (θ - \frac{π}{12}) = \frac{3}{4}$ ，则 $sin (2 θ + \frac{π}{3}) =$ （）

A、 $- \frac{7}{16}$ B、 $- \frac{1}{8}$ C、 $\frac{1}{8}$ D、 $\frac{7}{16}$

查看解析
12、为检测同学体能，学校从高一年级随机抽取了100名同学参加体能测试，并将成绩分数分成五组：第一组 $[45, 55)$ ，第二组 $[55, 65)$ ，第三组 $[65, 75)$ ，第四组 $[75, 85)$ ，第五组 $[85, 95]$ ，绘制成如图所示的频率分布直方图.已知第一、二组的频率之和为0.3，第一组和第五组的频率相同.

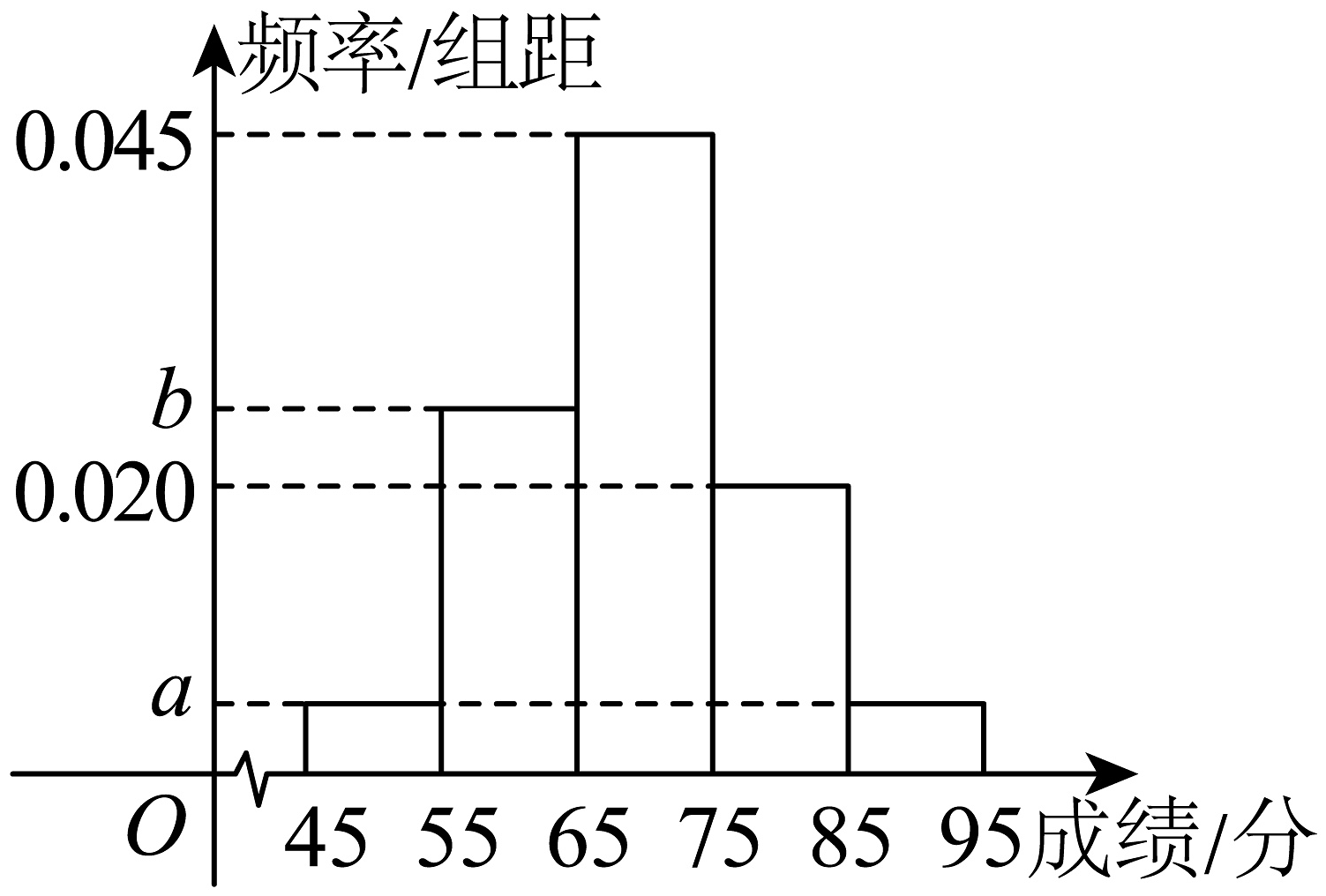(1)、估计这100名同学体能成绩分数的平均分和众数；

(2)、现从以上各组中用分层随机抽样的方法选取20人进行成绩分析，第二组同学成绩的平均数和方差分别为62和40，第四组同学成绩的平均数和方差分别为80和70，据此估计这次第二组和第四组所有同学成绩的方差.

查看解析
13、抛掷两枚质地均匀的硬币，设事件 $A =$ “第一枚硬币反面向上”，事件 $B =$ “第二枚硬币正面向上”，下列结论中正确的是（）

A、 $A$ 与 $B$ 为互斥事件 B、 $P (A) = P (B) = \frac{1}{4}$ C、 $A$ 与 $B$ 为相互独立事件 D、 $A$ 与 $B$ 互为对立事件

查看解析
14、已知 $\vec{a} = (- 2, 1, 3)$ ， $\vec{b} = (- 1, 2, 1)$ ，若 $\vec{a} ⊥ (\vec{a} - λ \vec{b})$ ，则实数λ的值为（）

A、2 B、 $- \frac{14}{3}$ C、 $\frac{14}{5}$ D、 $- 2$

查看解析
15、已知函数 $f (x) = x |x - a| + 2 x$

(1)、当 $a = 1$ 时，画出函数 $f (x)$ 的图象，根据图象写出单调递增区间；

(2)、若函数 $f (x)$ 为 $R$ 上的增函数，求实数 $a$ 的取值范围.

(3)、若当 $x \in [a, + \infty)$ ，不等式 $f (x) > 0$ 恒成立，求实数 $a$ 的范围；

查看解析
16、已知函数 $f (x)$ 是定义在 $(- 1, 1)$ 上的奇函数，当 $x \in (0, 1)$ 时， $f (x) = 2^{x}$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、求 $f (x)$ 的值域；

(3)、若不等式 $f (2 a) + f (1 - a) > 0$ ，求实数 $a$ 的取值范围.

查看解析
17、已知函数 $f (x) = \frac{4^{x} - 1}{4^{x} + 1}$ .

(1)、求函数 $f (x)$ 的定义域和值域；

(2)、判断并证明 $f (x)$ 的奇偶性.

查看解析
18、围建一个面积为360 $m^{2}$ 的矩形场地，要求矩形场地的一面利用旧墙（利用的旧墙需维修），其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为2m的进出口，如图．已知旧墙的维修费用为45元/m，新墙的造价为180元/m.设利用的旧墙长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）．试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

查看解析
19、已知函数 $f (x) = {(x - 1)}^{3}$ 的定义域为 $A$ ，函数 $g (x) = {(\frac{1}{2})}^{x}$ ， $(- 1 \leq x \leq 0)$ 的值域为 $B$ .

(1)、求 $A \cap B$ ；

(2)、若 $C = \{x| a \leq x \leq 2 a - 1\}$ ，且 $C \subseteq B$ ，求 $a$ 的取值范围.

查看解析
20、已知函数 $y = a x^{2} - 2 x - 1$ 在 $(- \infty, 1)$ 上是减函数，则 $a$ 的取值范围是.

查看解析

上一页 622 623 624 625 626 下一页跳转

	没有进步	有进步	合计
参与周末在校自主学习	35	130	165
未参与周末不在校自主学习	25	30	55
合计	60	160	220

$α$	0.10	0.05	0.010	0.005	0.001
$χ_{α}$	2.706	3.841	6.635	7.879	10.828

编号	1	2	3	4	5
学习时间x	30	40	50	60	70
数学成绩y	65	78	85	99	108