-
1、若直线与圆交于 , 两点,则弦长的取值范围为.
-
2、若椭圆 , 则该椭圆的焦点到短轴端点的距离为.
-
3、在棱长为1的正方体中,点为线段的中点,动点满足 , 其中 , 则( )A、 B、平面平面 C、存在点 , 使得 D、当时,平面截正方体的截面积为
-
4、已知圆 , 点是直线上一动点,过点作圆的切线 , , 切点分别是和 , 则下列说法错误的是( )A、圆上恰有一个点到直线的距离为 B、切线长的最小值为1 C、四边形面积的最小值为2 D、直线恒过定点
-
5、已知椭圆的左、右焦点分别为、 , 过作直线与椭圆相交于、两点, , 且 , 则椭圆的离心率为( )A、 B、 C、 D、
-
6、某圆锥母线长为 , 底面半径为2,则过该圆锥顶点的平面截此圆锥所得截面的面积最大时,此截面将底面圆周所分成的两段弧长之比(较短弧与较长弧之比)为( )A、 B、 C、 D、
-
7、如图,在四棱锥中,底面是边长为a的正方形,平面 . 若 , 则直线与平面所成的角的大小为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、已知点、 , 设过点的直线与的边交于点(其中点异于、两点),与边交于(其中点异于、两点),若设直线的斜率为.(1)、试用来表示点和的坐标;(2)、求的面积关于直线的斜率的函数关系式;(3)、当为何值时,取得最大值?并求此最大值.
-
9、如图,在直四棱柱中, , , .
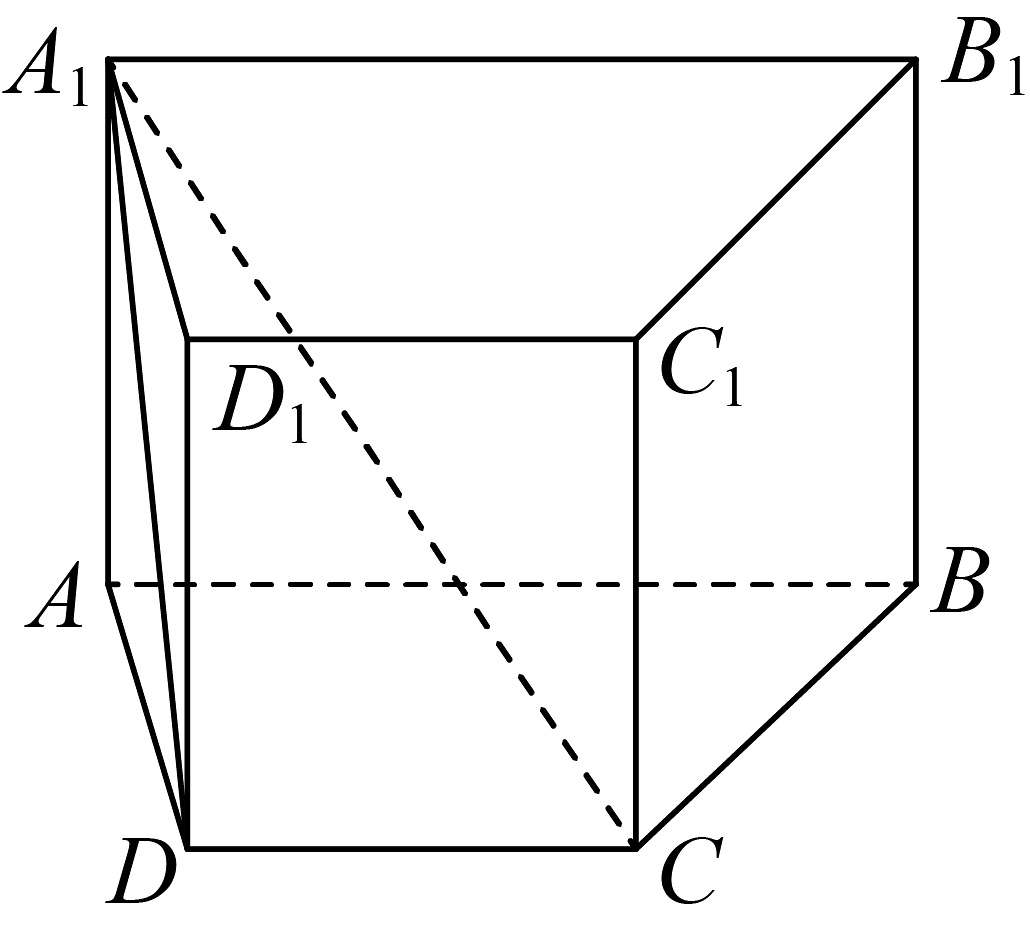 (1)、求证:平面;(2)、求平面与平面夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值. -
10、在锐角中,角A、B、C的对边分别为a、b,c,其面积为S,且 .(1)、求角A的大小;(2)、若 , 求S的取值范围.
-
11、为了解某年级学生对《居民家庭用电配置》的了解情况,校有关部门在该年级进行了一次问卷调查(共10道题),从该年级学生中随机抽取24人,统计了每人答对的题数,将统计结果分成[0,2),[2,4),[4,6),[6,8),[8,10]五组,得到如下频率分布直方图.

(1)估计这组数据的平均数(同一组中的数据用该组区间的中点值作代表);
(2)用分层随机抽样的方法从[4,6),[6,8),[8,10]的组别中共抽取12人,分别求出抽取的三个组别的人数;
(3)若从答对题数在[2,6)内的人中随机抽取2人,求恰有1人答对题数在[2,4)内的概率.
-
12、已知两直线和的交点为 .(1)、若直线过点且与直线平行,求直线的一般式方程;(2)、若圆过点且与相切于点 , 求圆的标准方程.
-
13、在四棱柱中,底面 , 底面是正方形, , , 为的中点,则异面直线与所成角的余弦值为 .
-
14、已知向量 , 若 , 则 .
-
15、数学美的表现形式不同于自然美或艺术美那样直观,它蕴藏于特有的抽象概念、公式符号、推理论证、思维方法等之中,揭示了规律性,是一种科学的真实美.在平面直角坐标系中,曲线就是一条形状优美的曲线,对于此曲线,下列说法正确的有( )A、曲线围成的图形的周长是 B、曲线围成的图形有条对称轴 C、若是曲线上任意一点,的最小值是 D、曲线上的任意两点间的距离不超过
-
16、下列给出的命题正确的是( )A、若直线l的方向向量为 , 平面的法向量为 , 则 B、两个不重合的平面的法向量分别是 , 则 C、若是空间的一组基底,则也是空间的一组基底 D、已知三棱锥 , 点P为平面ABC上的一点,且 , 则
-
17、已知点A,B,C,D,P,Q都在同一个球面上,为正方形,若直线PQ经过球心,且平面.则异面直线所成的角的最小值为( )A、 B、 C、 D、
-
18、在三棱锥中, , , , 则三棱锥的外接球的表面积为( )A、 B、 C、 D、
-
19、如图正方体的棱长为a,以下结论中,错误的是( )
 A、异面直线与所成的角为 B、直线与垂直 C、直线与平行 D、直线与平行
A、异面直线与所成的角为 B、直线与垂直 C、直线与平行 D、直线与平行 -
20、在空间中,若向量 , , 共面,则( )A、4 B、2 C、 D、