版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、某植物园种植一种观赏花卉，这种观赏花卉的高度（单位： $cm$ ）介于 $[15, 25]$ 之间，现对植物园部分该种观赏花卉的高度进行测量，所得数据统计如图所示.

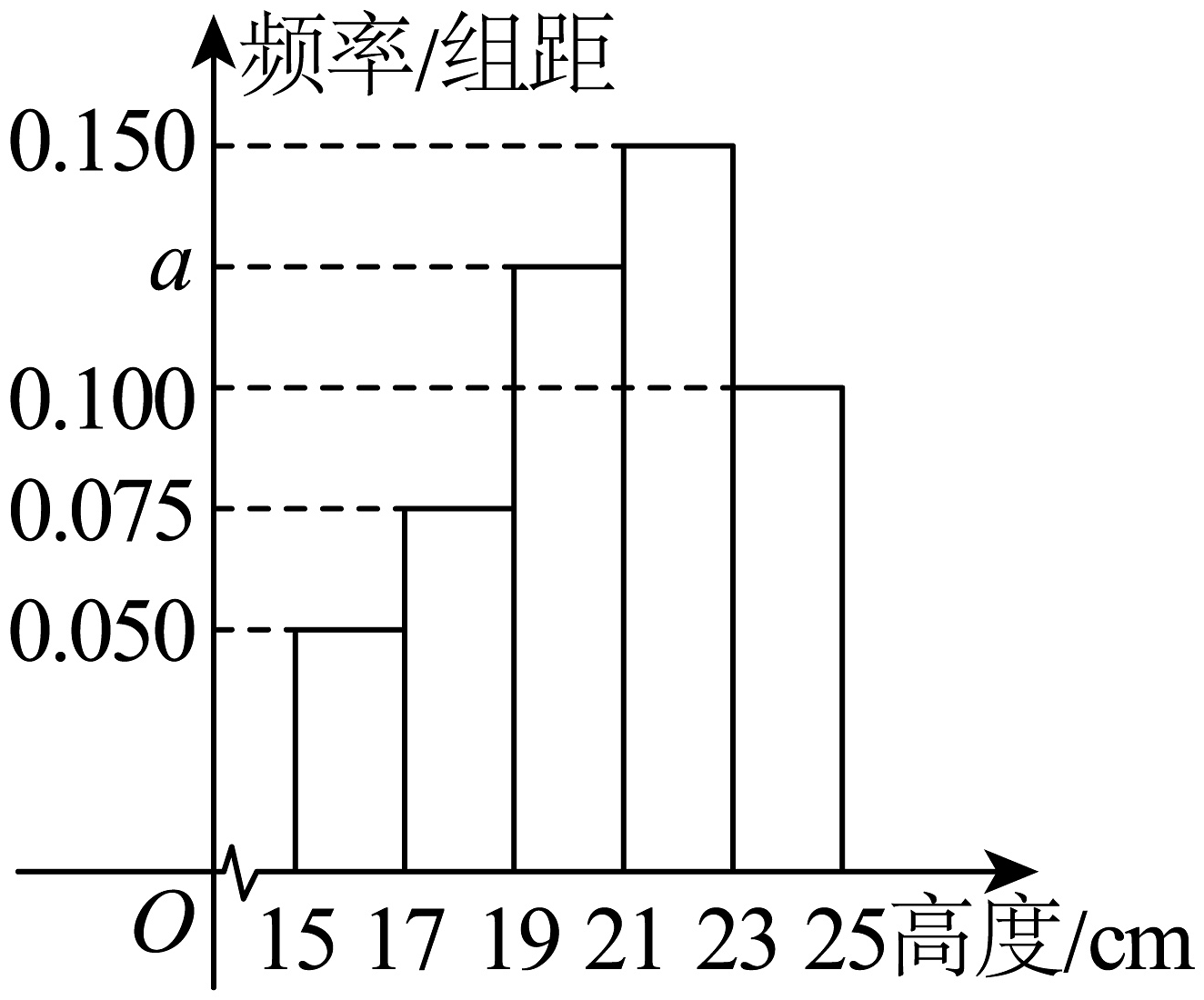(1)、求 $a$ 的值；

(2)、若从高度在 $[15, 17)$ 和 $[17, 19)$ 中分层抽样抽取5株，在这5株中随机抽取3株，记高度在 $[15, 17)$ 内的株数为 $X$ ，求 $X$ 的分布列及数学期望 $E (X)$ ；

(3)、以频率估计概率，若在所有花卉中随机抽取3株，记高度在 $[15, 17)$ 内的株数为 $Y$ ，求 $Y$ 的数学期望.

查看解析
2、如图，在底面 $A B C D$ 是矩形的四棱锥 $P - A B C D$ 中， $A B = 1, B C = 2, P A = P D = \sqrt{6}$ ，点 $P$ 在底面 $A B C D$ 上的射影为点 $O (O$ 与 $B$ 在直线 $A D$ 的两侧 $)$ ，且 $P O = 2$ .

(1)、求证： $A O ⊥ P D$ ；

(2)、求平面 $A B P$ 与平面 $B C P$ 夹角的余弦值.

查看解析
3、已知双曲线C： $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， $O$ 为原点，若以 $|F_{1} F_{2}|$ 为直径的圆与 $C$ 的渐近线的一个交点为 $P$ ，且 $|F_{1} P| = \sqrt{3} |O P|$ ，则 $C$ 的离心率为.

查看解析
4、如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $O$ 为正方体的中心， $M$ 为 $D D_{1}$ 的中点， $F$ 为侧面正方形 $A A_{1} D_{1} D$ 内一动点，且满足 $B_{1} F / /$ 平面 $B C_{1} M$ ，则（）

A、三棱锥 $D_{1} - D C B$ 的外接球表面积为 $12 π$ B、动点 $F$ 的轨迹的线段为 $\frac{π}{2}$ C、三棱锥 $F - B C_{1} M$ 的体积为定值 D、若过 $A$ ， $M$ ， $C_{1}$ 三点作正方体的截面 $Ω$ ， $Q$ 为截面 $Ω$ 上一点，则线段 $A_{1} Q$ 长度的取值范围为 $[\frac{2 \sqrt{6}}{3}, 2 \sqrt{2}]$

查看解析
5、已知 $A B$ 是圆O： $x^{2} + y^{2} = 2$ 的直径，M，N是圆O上两点，且 $∠ M O N = 120 °$ ，则 $(\vec{O M} + \vec{O N}) \cdot \vec{A B}$ 的最小值为（）

A、0 B、-2 C、-4 D、 $- 4 \sqrt{3}$

查看解析
6、已知数列 $a_{n} = 2 n - 1,$ $b_{n} = 3 n - 2$ ，则由这两个数列公共项从小到大排列得到的数列为 $\{c_{n}\}$ ，则数列 $\{c_{n}\}$ 的通项公式为（）

A、 $c_{n} = 3 n - 2$ B、 $c_{n} = 4 n - 1$ C、 $c_{n} = 5 n - 3$ D、 $c_{n} = 6 n - 5$

查看解析
7、已知函数 $f (x) = \frac{- 2 x}{x^{2} + 2}$ .

(1)、判断 $f (x)$ 的奇偶性；

(2)、用单调性定义证明 $f (x)$ 在 $(- 1, 1)$ 上单调递减；

(3)、若 $f (x)$ 的定义域为 $(- 1, 1)$ ，解不等式 $f (x^{2}) + f (\frac{1}{6} - \frac{5}{6} x) > 0$ .

查看解析
8、已知函数 $f (x) = 2 \sqrt{3} \sin x \cos x - \cos^{2} x + \sin^{2} x$ ， $x \in R$ ．

(1)、求 $f (x)$ 的单调递增区间；

(2)、当 $x \in [\frac{π}{6}, \frac{5 π}{12}]$ 时，求 $f (x)$ 的最大值和最小值；

(3)、当 $x \in [\frac{π}{6}, \frac{5 π}{12}]$ 时，方程 $f (x) = k$ 恰有两个不同的实数根，求实数k的取值范围．

查看解析
9、摩天轮是一种大型转轮状的机械建筑设施，乘客坐在摩天轮的座舱（挂在轮边缘）里慢慢地往上转，可以从高处俯瞰四周景色.已知某摩天轮的半径为60米，其中心距离地面70米，开启后沿逆时针方向匀速旋转，乘客在座舱转到距离地面最近的位置进舱，转一周大约需要30分钟．

(1)、设乘客P坐上摩天轮的座舱，开始转动t分钟后距离地面高度为h米，求在转动一周的过程中，h关于t的函数解析式；

(2)、摩天轮在转动一圈的过程中，乘客距离地面超过100米的时间有多长？

查看解析
10、已知 $f (α) = \frac{\sin (7 π - α) \cdot \cos (α + \frac{3 π}{2}) \cdot \cos (3 π + α)}{\sin (α - \frac{3 π}{2}) \cdot \cos (α + \frac{5 π}{2}) \cdot \tan (α - 5 π)}$ .
（1）化简 $f (α ）$ ；
（2）若 $α$ 是第二象限，且 $\cos (\frac{3 π}{2} + α) = \frac{1}{7}$ ，求 $f (α)$ 的值．

查看解析
11、已知 $0 < α < \frac{π}{2}$ ， $\cos (α + \frac{π}{4}) = \frac{1}{3}$ ．若 $- \frac{π}{2} < β < 0$ ， $\cos (\frac{β}{2} - \frac{π}{4}) = \frac{\sqrt{3}}{3}$ ，则 $α - β$ 的值是．

查看解析
12、已知函数 $f (x) = cos 2 x cos φ - sin 2 x sin φ$ $(0 < φ < \frac{π}{2})$ 的图象的一个对称中心为 $(\frac{π}{6},0)$ ，则下列说法正确的是（）

A、直线 $x = \frac{5}{12} π$ 是函数 $f (x)$ 的图象的一条对称轴 B、函数 $f (x)$ 在 $[0, \frac{π}{6}]$ 上单调递减 C、函数 $f (x)$ 的图象向右平移 $\frac{π}{6}$ 个单位可得到 $y = cos 2 x$ 的图象 D、函数 $f (x)$ 在 $[0, \frac{π}{2}]$ 上的最小值为－1

查看解析
13、如图是下列四个函数中某一个的部分图象，则该函数为（）

A、 $f (x) = \frac{x}{\ln |x + 2|}$ B、 $f (x) = \frac{x + 1}{e^{x + 1} - 1}$ C、 $f (x) = \frac{x^{3}}{{(x + 1)}^{2}}$ D、 $f (x) = \frac{x}{{(x + 1)}^{2}}$

查看解析
14、“拐点”又称“反曲点”，是曲线上弯曲方向发生改变的点.设 $φ^{'} (x)$ 为函数 $φ (x)$ 的导数，若 $α$ 为 $φ^{'} (x)$ 的极值点，则 $(α, φ (α))$ 为曲线 $y = φ (x)$ 的拐点.
已知曲线C： $y = x^{3} - 3 x^{2} + 1$ .

(1)、求C的拐点坐标；

(2)、证明：C关于其拐点对称；

(3)、设 $l$ 为C在其拐点处的切线，证明：所有平行于 $l$ 的直线都与C有且仅有一个公共点.

查看解析
15、某学校组织竞赛，有A，B两类问题可供选择，其中A问题答对可得5分，答错0分，B问题答对只可得3分，但答错有2分，现小明与小红参加此竞赛，小红答对2种问题的概率均为0.5，小明答对A，B问题的概率分别为0.3，0.7

(1)、小红一共参与回答了2题，记X为小红的累计得分，求X的分布列

(2)、小明也参与回答了2道问题，记Y为小明的累计得分，求该如何选择问题，使得E[Y]最大．

查看解析
16、已知点A(-2，0)，B(2，0)，动点M $(x, y)$ 满足直线AM与BM的斜率之积为 $\frac{1}{2}$ ，记M的轨迹为曲线C.

(1)、求C的方程，并说明C是什么曲线；

(2)、若直线 $l : y = x - 3$ 和曲线C相交于E，F两点，求 $| E F |$ .

查看解析
17、已知数列 $\{a_{n}\}$ 满足： $a_{1} = 2, a_{n + 1} = a_{n} + 2^{n}$ .
（1）求 $\{a_{n}\}$ 的通项公式；
（2）若 $b_{n} = \log_{2} a_{n}, T_{n} = \frac{1}{b_{1} b_{2}} + \frac{1}{b_{2} b_{3}} + \dots + \frac{1}{b_{n} b_{n + 1}}$ ，求 $T_{n}$ .

查看解析
18、函数 $y = |- x^{2} + 4 x + 5|$ 的单调递增区间是．

查看解析
19、已知 $(a x - 2) {(x + \frac{2}{x})}^{5}$ 的展开式中的常数项为240，则 $a =$ ．

查看解析
20、有6本不同的书，按下列方式进行分配，其中分配种数正确的是（）

A、分给甲、乙、丙三人，每人各2本，有15种分法 B、分给甲、乙、丙三人，一人4本，另两人各1本，有180种分法 C、分给甲、乙每人各2本，分给丙、丁每人各1本，有180种分法 D、分给甲、乙、丙、丁四人，两人各2本，另两人各1本，有1080种分法

查看解析

上一页 575 576 577 578 579 下一页跳转