-
1、已知点 , 则向量的坐标为 .
-
2、设点是所在平面内一点,则下列说法正确的是( )A、若 , 则点是边的中点 B、若 , 则点在边的延长线上 C、若 , 则点是的重心 D、若 , 且 , 则的面积是的面积的
-
3、已知是边长为的等边三角形,是边上的动点,是边的中点,则的取值范围是( )A、 B、 C、 D、
-
4、在中,内角、、所对的边分别为、、 , 若 , 则的形状一定为( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形
-
5、若 , 则的大小关系是( )A、 B、 C、 D、
-
6、已知为第四象限角, , 则( )A、 B、 C、 D、
-
7、函数的定义域是( )A、 B、 C、 D、
-
8、 , , 则( )A、 B、 C、 D、
-
9、已知实数 , 当取得最小值时,则的值为 .
-
10、已知平行六面体 , , , , , 设 , , ;
 (1)、试用表示;(2)、求的长度;(3)、求直线与所成角的余弦值.
(1)、试用表示;(2)、求的长度;(3)、求直线与所成角的余弦值. -
11、如图,两个相同的正四棱台密闭容器内装有纯净水, , 图1中水面高度恰好为棱台高度的 , 图2中水面高度为棱台高度的 , 若图1和图2中纯净水的体积分别为 , 则( )
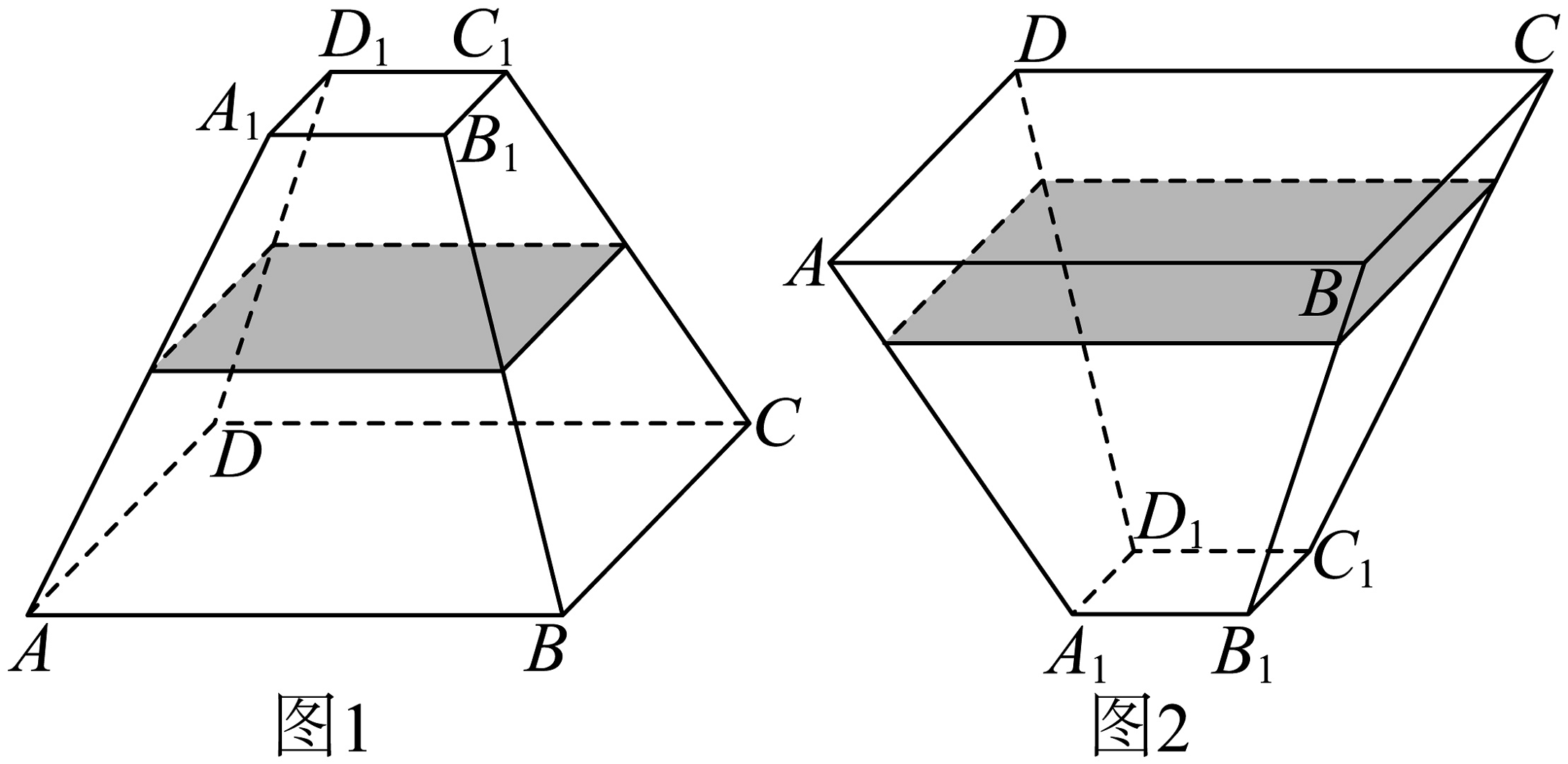 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知椭圆经过点 , 其右顶点为 , 上顶点为为坐标原点,且离心率为.(1)、设在点处的切线 , 其斜率为的斜率为 , 求的值;(2)、过在第一象限的点作椭圆的切线,分别与轴,轴交于点 , 且为线段的中点,记以点为中心,轴,轴为对称轴,且过点的椭圆为 , 依此类推, , 过椭圆在第一象限的点作椭圆的切线,分别与轴,轴交于点 , 且为线段的中点,记以点为中心,轴,轴为对称轴,且过点的椭圆为 , 由此得到一系列椭圆.
(i)求的方程;
(ii)过点作直线与椭圆分别交于 , 求证:.
(附:若为椭圆上一点,则椭圆在点处的切线方程为:)
-
13、已知函数和的图象在处有相同的切线.(1)、求实数和的值;(2)、求函数的极值;(3)、当时,不等式恒成立,求实数的取值集合.
-
14、在某游戏中,玩家可通过祈愿池获取新角色和新武器.该游戏的角色活动祈愿池的祈愿规则为:
①每次祈愿获取五星角色的概率;
②若连续89次祈愿都没有获取五星角色,那么第90次祈愿必定通过“保底机制”获取五星角色;
③除触发“保底机制”外,每次祈愿相互独立.
设随机变量表示在该祈愿池中连续祈愿直至获取五星角色为止的祈愿次数.
(1)、求的解析式;(2)、求的数学期望.参考数据:
-
15、如图四棱锥中,底面是边长为2的等边三角形,且 , , 点在棱上.
 (1)、求证:平面平面;(2)、若 , 求直线与平面所成角的正弦值.
(1)、求证:平面平面;(2)、若 , 求直线与平面所成角的正弦值. -
16、在中,角的对边分别为 , 且是与的等差中项.
 (1)、求;(2)、如图所示,为平面上一点,与构成一个四边形 , 且 , 若 , 求的最大值.
(1)、求;(2)、如图所示,为平面上一点,与构成一个四边形 , 且 , 若 , 求的最大值. -
17、已知是棱长为的正四面体 , 设的四个顶点到平面的距离所构成的集合为 , 若中元素的个数为 , 则称为的阶等距平面,为的阶等距集.如果为的1阶等距平面且1阶等距集为 , 则符合条件的有个,的所有可能取值构成的集合是.
-
18、已知函数 , 数列满足 , 给出下列两个条件:①函数是递减函数;②数列是递减数列.试写出一个满足条件②但不满足条件①的函数的解析式:.
-
19、已知公式 , 其中是虚数单位,根据此公式计算的虚部是.
-
20、已知点是抛物线的焦点,直线经过点交抛物线于两点,与准线交于点 , 且为中点,则下面说法正确的是( )A、 B、直线的斜率是 C、 D、设原点为 , 则的面积为