-
1、已知向量在正方形网格中的位置如图所示,若网格纸上小正方形的边长为1,则;

-
2、曲线是平面内与三个定点和的距离的和等于的点的轨迹,为上一点,则( )A、曲线关于轴对称 B、存在点P,使得 C、面积的最大值是1 D、存在点 , 使得为钝角
-
3、已知等差数列与等比数列的前项和分别为 , 则下列结论中正确的是( )A、数列是等比数列 B、可能为 C、数列是等差数列 D、数列是等比数列
-
4、有一组样本数据 , , …, , 由这组数据得到新样本数据 , , …, , 其中(为非零常数,则( )A、两组样本数据的样本平均数相同 B、两组样本数据的样本中位数相同 C、两组样本数据的样本标准差相同 D、两组样本数据的样本极差相同
-
5、有四张卡片,每张卡片的一面上写着英文字母,则另外一面上写着数字.现在规定:当牌的一面写着数字7时,另外一面必须写着字母.你的任务是:为了检验下面4张卡牌是否有违反规定的写法,你需要翻看哪些牌?( )
 A、①② B、②③ C、②④ D、④③
A、①② B、②③ C、②④ D、④③ -
6、设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量取值x1、x2、x3、x4、x5的概率均为0.2,随机变量取值、、、、的概率也均为0.2,若记、分别为、的方差,则( )A、> B、= C、< D、与的大小关系与x1、x2、x3、x4的取值有关
-
7、已知 , 且 , 则( )A、 B、 C、 D、
-
8、已知空间向量满足 , 则( )A、 B、1 C、0 D、
-
9、函数的最小正周期为( )A、 B、 C、 D、
-
10、把函数的图象按向量平移,得到的图象,则( )A、 B、 C、 D、
-
11、若集合 , 则( )A、 B、 C、 D、
-
12、牛顿法是17世纪牛顿在《流数法与无穷级数》一书中,给出了高次代数方程的一种数值解法.具体步骤如下:设是函数的一个零点,任取作为的初始近似值,过点作曲线的切线 , 设与轴交点的横坐标为 , 并称为的1次近似值;过点作曲线的切线 , 设与轴交点的横坐标为 , 称为的2次近似值;一直继续下去,得到.一般地,过点作曲线的切线 , 记与轴交点的横坐标为 , 并称为的次近似值,称数列为牛顿数列.(1)、若函数的零点为.求的2次近似值;(2)、设是函数的两个零点,数列为函数的牛顿数列,数列满足.
(i)求证:数列为等比数列;
(ii)证明:.
-
13、已知分别为椭圆的左,右焦点,为的上顶点,点为椭圆上的一个动点,且三角形面积的最大值为1,焦距为2.
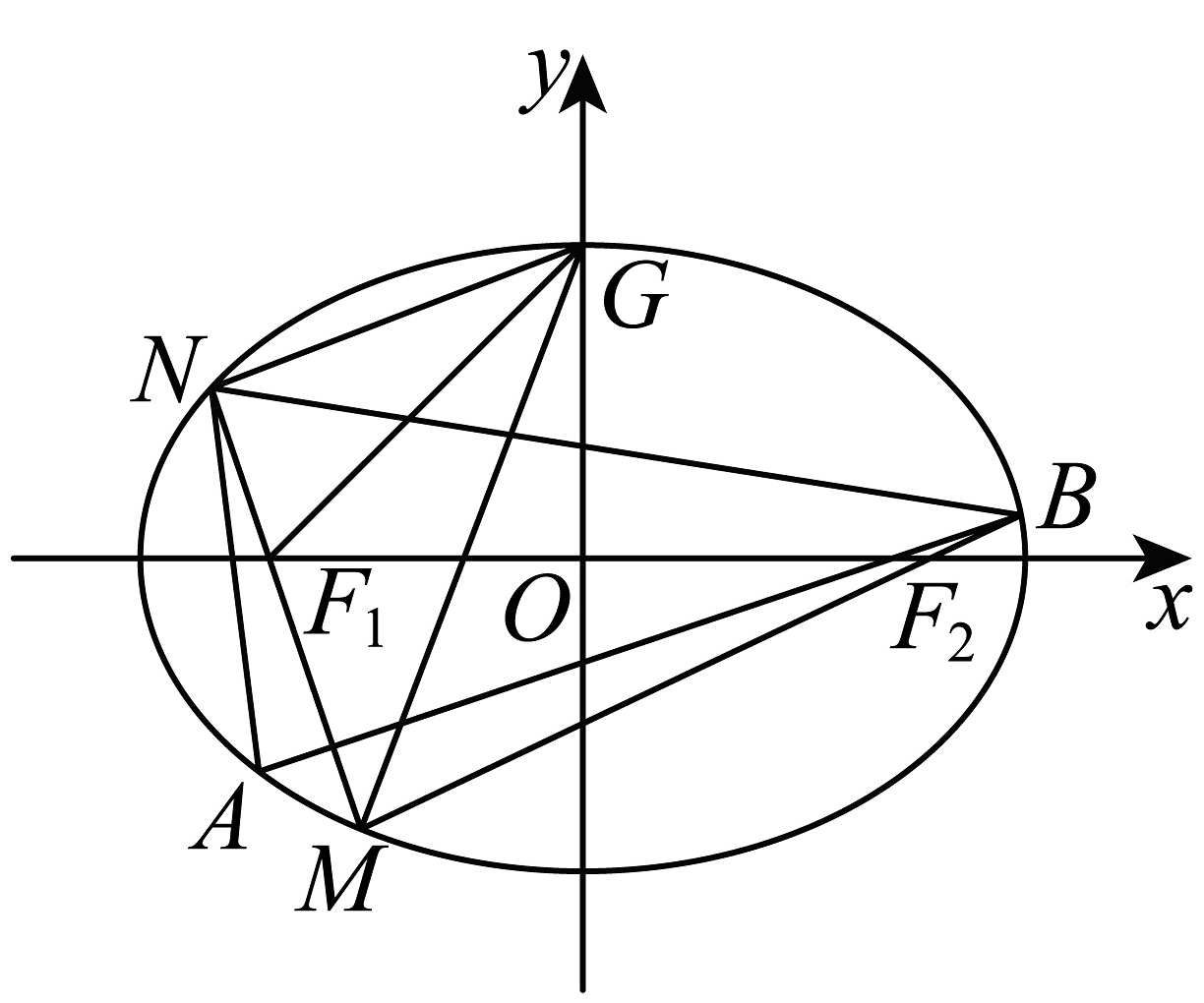 (1)、求椭圆的标准方程;(2)、如图,过点作两直线分别与椭圆相交于点和点.
(1)、求椭圆的标准方程;(2)、如图,过点作两直线分别与椭圆相交于点和点.(i)若点不在坐标轴上,且 , 求直线的方程;
(ii)若直线斜率都存在,且 , 求四边形面积的最小值.
-
14、某系统配置有个元件(为正整数),每个元件正常工作的概率都是 , 且各元件是否正常工作相互独立.如果该系统中有一半以上的元件正常工作,系统就能正常工作.现将系统正常工作的概率称为系统的可靠性.(1)、当时,求该系统正常工作的概率;(2)、现在为了改善原系统的性能,在原有系统中增加两个元件,试问增加两个元件后的新系统的可靠性是提高了,还是降低了?请给出你的结论,并说明理由.
-
15、如图,在三棱柱中,平面平面 , , , , , 为线段上一点,且.
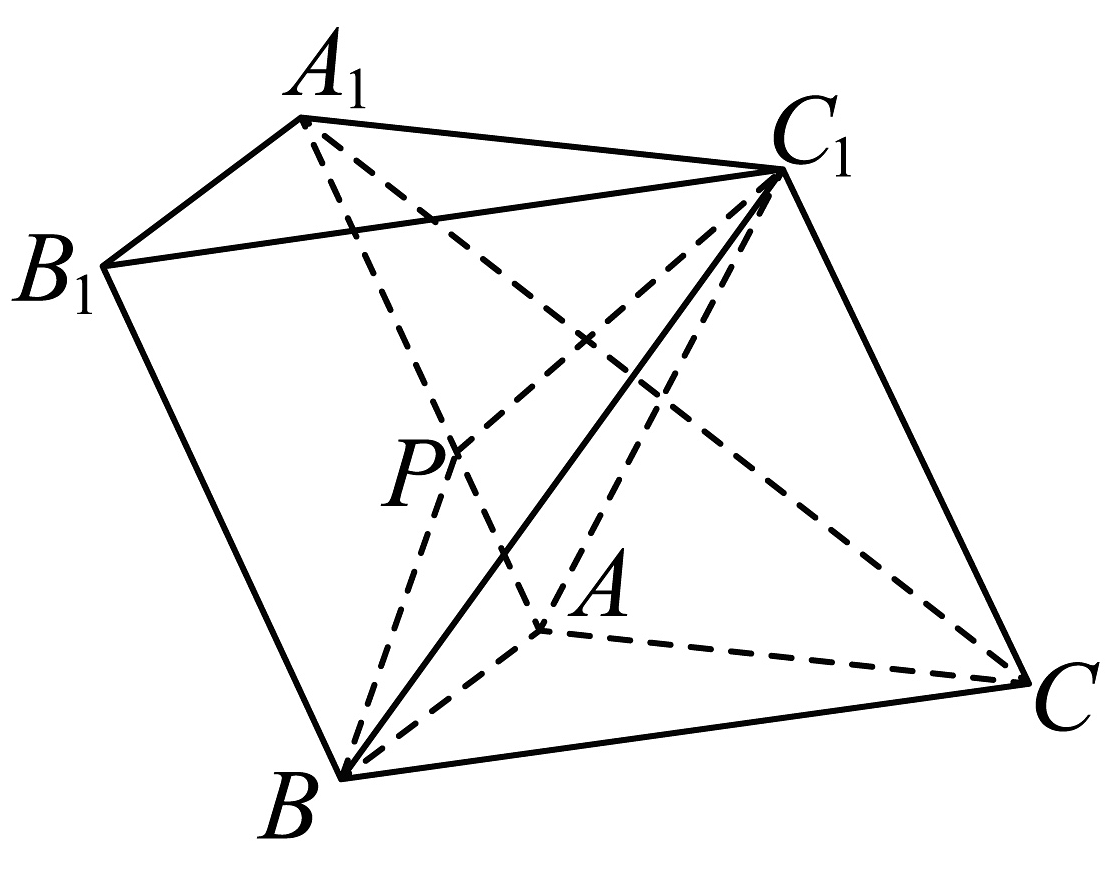 (1)、求证:;(2)、是否存在实数 , 使得平面与平面的夹角余弦值为?若存在,求出实数的值;若不存在,请说明理由.
(1)、求证:;(2)、是否存在实数 , 使得平面与平面的夹角余弦值为?若存在,求出实数的值;若不存在,请说明理由. -
16、已知正项数列的前项和为 , 且.(1)、求数列的通项公式;(2)、设 , 求数列前项的和.
-
17、已知是双曲线的左,右焦点,过左焦点的直线交双曲线左支于两点(其中在轴上方,在轴下方),的内切圆半径为的内切圆半径为.若 , 则直线的斜率等于.
-
18、在中,内角的对边分别是 , 满足.若 , 则的面积的最大值是.
-
19、已知随机变量服从正态分布 , 且 , 则.
-
20、平面直角坐标系中,定义为两点 , 的“切比雪夫距离”;又设点及直线上任意一点 , 称的最小值为点到直线的“切比雪夫距离”,记作.则下列结论正确的是( )A、当时, B、当时, C、对任意三点恒成立 D、动点与定点满足的轨迹围成的面积是16