-
1、某校有1000人参加某次模拟考试,其中数学考试成绩近似服从正态分布(),试卷满分150分,统计结果显示数学成绩优秀(高于120分)的人数占总人数的 , 则此次数学考试成绩在90分到105分(含90分和105分)之间的人数约为( )A、150 B、200 C、300 D、400
-
2、已知f(x)是定义在R上的偶函数,且在区间上单调递增,若实数a满足 , 则a的取值范围是( )A、 B、 C、 D、
-
3、在复平面内,O为坐标原点,复数 , 对应的向量分别是 , , 则对应的复数为( )A、 B、 C、 D、
-
4、已知全集 , , 则集合( )A、 B、 C、 D、
-
5、如图所示,在四棱锥中,底面为矩形, , , , , 分别是 , 的中点.
 (1)、求证:平面;(2)、若平面平面 , 求直线与平面所成角的余弦值.
(1)、求证:平面;(2)、若平面平面 , 求直线与平面所成角的余弦值. -
6、设 , , 若 , 则的最小值为 , 此时的值为.
-
7、我国古代数学典籍九章算术中有一种名为“羡除”的几何体,它由古代的隧道形状抽象而来.如图所示,在五面体中, , 四边形 , , 为等腰梯形,且平面平面.其中 , , (),且到平面的距离为 , 和的距离为 , 若 , , , , , 则该“羡除”的体积为.

-
8、已知集合 , 且 , 则实数的值为 .
-
9、函数在区间上的图象是一条连续不断的曲线,且满足 , 函数的图象关于点对称,则( )A、的图象关于点对称 B、8是的一个周期 C、一定存在零点 D、
-
10、已知函数的图象过点 , 且两条相邻对称轴之间的距离为 , 则下列说法正确的是( )A、 B、在上单调递增 C、直线为函数图象的一条对称轴 D、在上的值域为
-
11、几何学史上有一个著名的米勒问题:“设是锐角的一边上的两点,试在边上找一点 , 使得最大.”如图,其结论是:点为过两点且和射线相切的圆的切点.根据以上结论解决以下问题:在平面直角坐标系中,给定两点 , 点在轴上移动,则的最大值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知等差数列的前项和为 , 若 , 则( ).A、4 B、 C、 D、6
-
13、已知方程表示的曲线是椭圆,则实数的取值范围是( ).A、 B、 C、 D、
-
14、样本数据15,13,12,31,29,25,43,19,17,38的中位数为( ).A、19 B、22 C、21 D、18
-
15、已知椭圆:的左焦点为 , 椭圆上任意一点到的距离最大值为6.(1)、求椭圆的方程;(2)、过原点且斜率为的直线与椭圆交于M,N两点.
(i)当时,设直线 , 的斜率分别是 , , 求证:为定值;
(ⅱ)过点作垂直于的直线交于 , 交圆:于P,Q两点,记 , 的面积分别为 , 求的取值范围.
-
16、如图,在矩形纸片中, , , 沿将折起,使点D到达点P的位置,点P在平面的射影H落在边上.
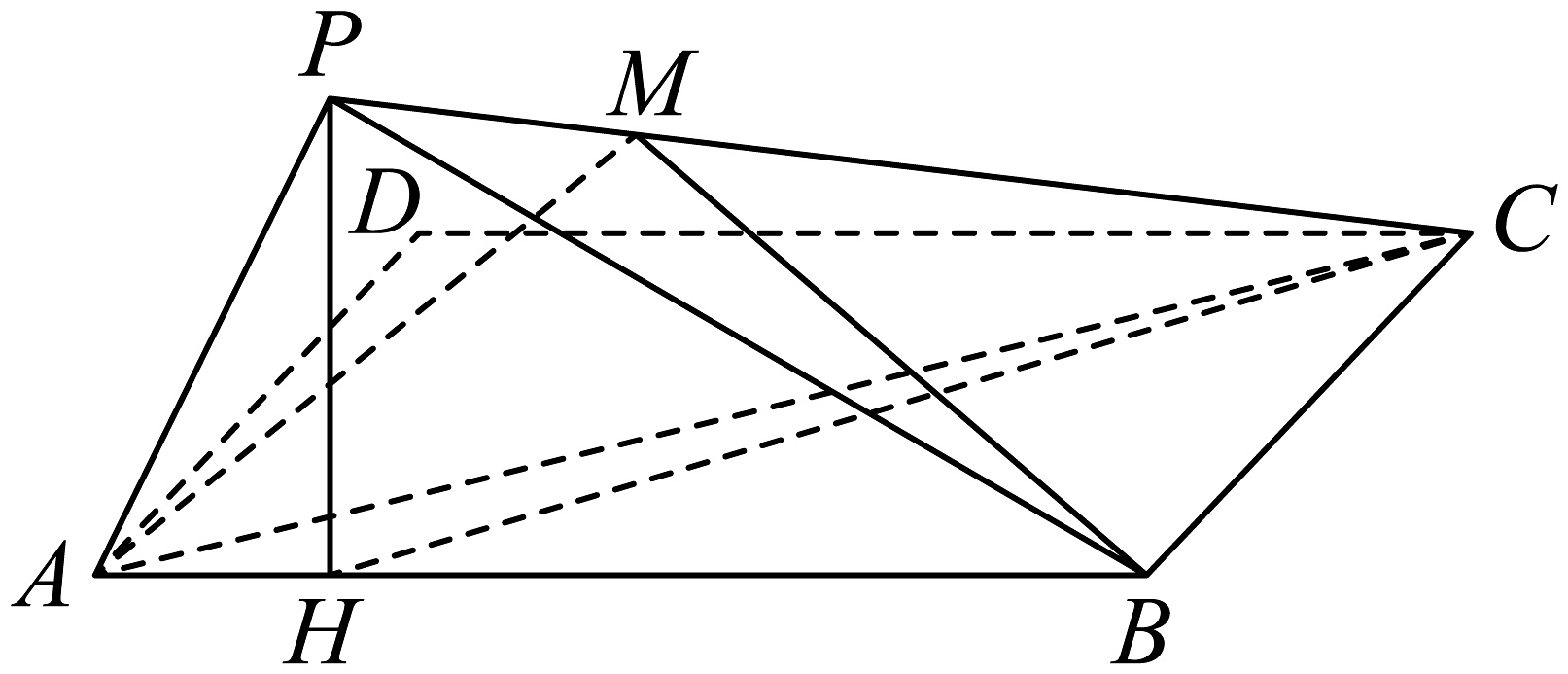 (1)、求三棱锥的体积;(2)、若M是棱上的一个动点,是否存在点M,使得平面与平面的夹角正切值为 , 若存在,求点M到平面的距离;若不存在,请说明理由.
(1)、求三棱锥的体积;(2)、若M是棱上的一个动点,是否存在点M,使得平面与平面的夹角正切值为 , 若存在,求点M到平面的距离;若不存在,请说明理由. -
17、已知函数.(1)、当时,求曲线在点处的切线方程;(2)、当时,设 , 讨论函数的单调性;(3)、若函数在上有且仅有2个零点,求实数的取值范围.
-
18、某汽车配件厂生产了一种塑胶配件,质检人员在这批配件中随机抽取了100个,将其质量指标值(单位:分)作为一个样本,得到如图所示的频率分布直方图.
 (1)、求的值;(2)、求这组数据的平均数(同一组中的数据用该组区间的中点值为代表);(3)、当配件的质量指标值不小于80分时,配件为“优秀品”,以频率估计概率.在这批产品中有放回地随机抽取3件产品,随机变量表示:抽得的产品为“优秀品”的个数,求的分布列及数学期望.
(1)、求的值;(2)、求这组数据的平均数(同一组中的数据用该组区间的中点值为代表);(3)、当配件的质量指标值不小于80分时,配件为“优秀品”,以频率估计概率.在这批产品中有放回地随机抽取3件产品,随机变量表示:抽得的产品为“优秀品”的个数,求的分布列及数学期望. -
19、记的内角A,B,C所对的边分别为a,b,c,且.(1)、求B;(2)、设D为边的中点,若 , , 求的面积.
-
20、已知圆的方程为 , 直线的方程为 , 直线被圆截得的弦中长度为整数的共有条.