-
1、已知过抛物线焦点的直线与该抛物线交于两点,若 , 则的最大值为( )A、2 B、3 C、4 D、6
-
2、在中,角所对的边分别为 , 已知 , 则下列结论一定正确的是( )A、 B、 C、 D、
-
3、已知函数在区间上单调递增,则的最小值为( )A、1 B、2 C、3 D、4
-
4、将一个棱长为6cm的正方体铁块熔铸成一个底面半径为3cm的圆锥体零件,则该圆锥体零件的高约为( )(取)A、8cm B、12cm C、16cm D、24cm
-
5、已知 , 向量与的夹角为 , 则( )A、1 B、 C、 D、
-
6、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
7、已知椭圆和双曲线有相同的焦点为两曲线在第一象限的交点,分别为曲线的离心率.若 , 则的最小值为( )A、 B、 C、 D、
-
8、给定实数 , 对于正整数 , 设数列满足每一项取1的概率为 , 取0的概率为 , 且各项取值相互独立.如果数列中的0将数列分成(项、项、…、项)全为1 的连续段,则记 , 特别地,定义 , 例如,时,.(1)、时,记随机变量求的概率.(2)、对于数列 , 定义为:若 , 则它是最大的正整数 , 使;若 , 则它为0,例如,时,.
(i)时,求随机变量的分布及数学期望;
(ii)求随机变量的数学期望.
(3)、当时,求随机变量的数学期望. -
9、已知函数(1)、若函数在定义域上单调递增,求实数a的取值范围;(2)、设是的两个极值点,证明:
(i);
(ii)
-
10、在平面直角坐标系中,圆的方程为: , 定点 , B是圆C上任意一点,线段 BF的垂直平分线l 和半径BC 相交于点 T.(1)、求点的轨迹的方程;(2)、轨迹W与x轴的交点为M,N(点N在点M 右侧),直线PQ与轨迹W 交于P,Q两点(异于M,N),MP的斜率为 , NQ的斜率为且 , 与的面积分别为 , , 求的最大值.
-
11、如图,圆柱中,是底面圆上的一条直径, , 分别是底面 , 圆周上的一点, , , 且点不与 , 两点重合.
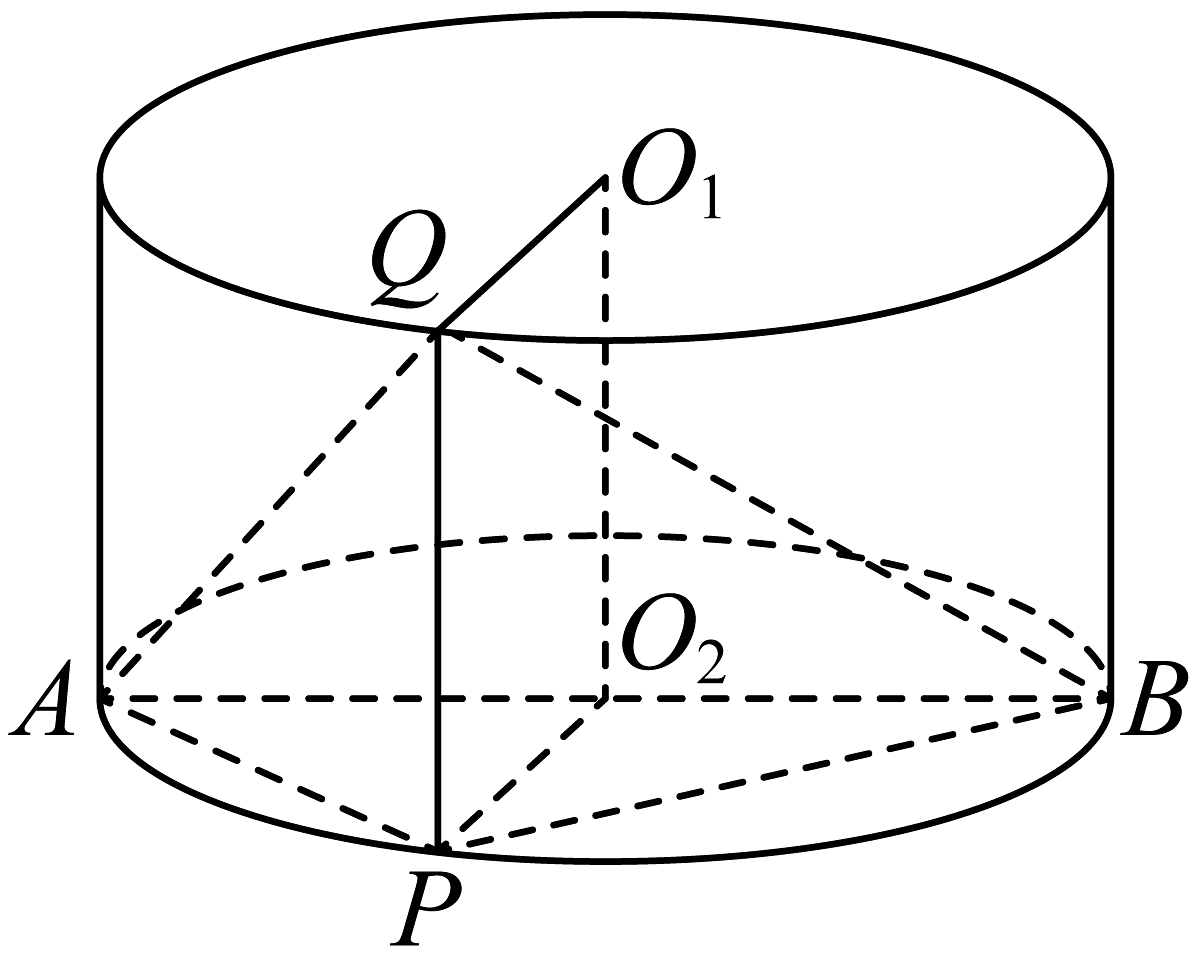 (1)、证明:平面平面;(2)、若二面角为 , 求直线与平面所成角的正弦值.
(1)、证明:平面平面;(2)、若二面角为 , 求直线与平面所成角的正弦值. -
12、记的内角的对边分别为 . 已知 , D为边上的靠近点C的三等分点.(1)、求角;(2)、求 .
-
13、不等式对任意成立,则实数的取值范围是.
-
14、已知为奇函数,则实数a的值是 .
-
15、已知等差数列的前n项和为若则
-
16、已知双曲线的左、右焦点分别为 , 左、右顶点分别为 , 过的直线与双曲线的右支交于两点(在第一象限),中点为 , 的内切圆圆心分别为 , 半径分别为 , 则下列结论正确的是( )A、三点共线 B、直线斜率存在时, C、若 , 则直线的斜率为 D、的取值范围是
-
17、在△ABC中,内角A,B,C所对的边分别为a,b,c,点M是△ABC所在平面上一点,且则下列说法正确的是( )A、若 , 则M在内部 B、若 , 则M为的重心 C、若 , 则的面积是面积的 D、若 , M为外接圆圆心,则
-
18、设的极差为 , 平均值为 , 中位数为m,方差为 , , 其中的极差为 , 平均值为 , 中位数为 , 方差为 , 则( )A、 B、 C、 D、
-
19、设正整数其中 , 记 , 则下列说法错误的是( ).A、ω(10)=2. B、ω(16n+5)=ω(4n+3). C、ω(8n+5)=ω(4n+5). D、若n<256且ω(n)=3,则符合条件的n有56个.
-
20、已知一组数据0,9,7,4,5,从1到10中的整数里随机选择2个不同的数加入这组数据,则得到的新数据与原数据中位数相同的概率为( )A、 B、 C、 D、