相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、如图中的图象所表示的函数的解析式为( )
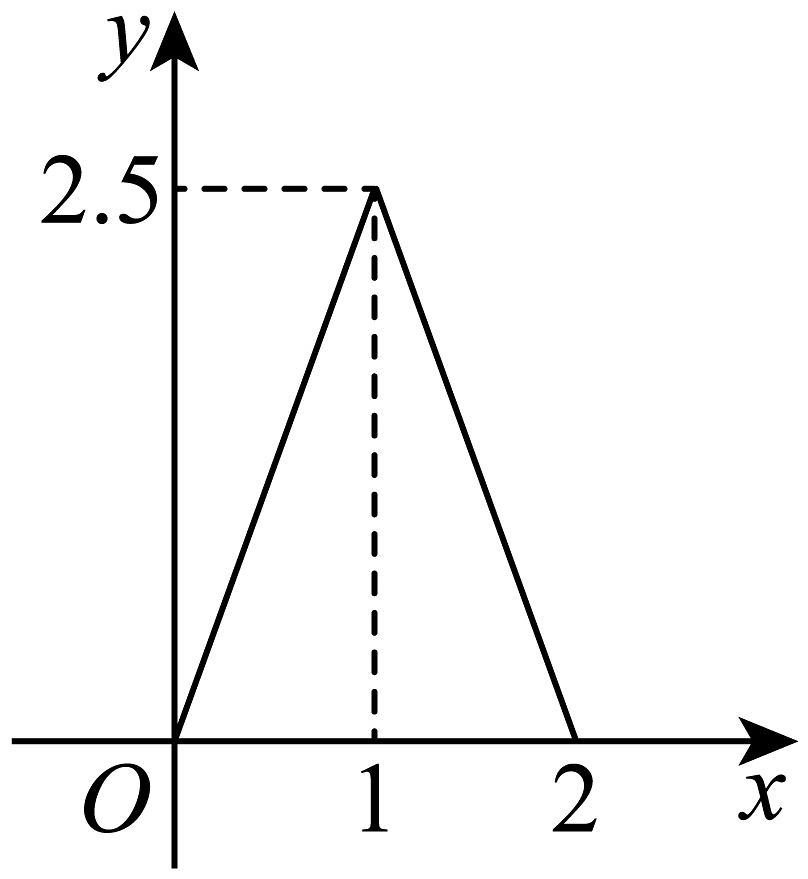 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图所示,平行六面体中, .
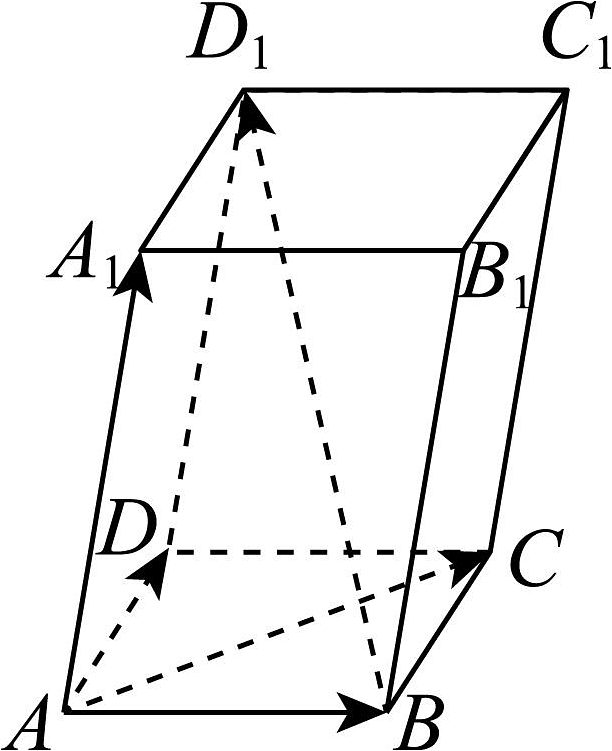 (1)、用向量表示向量 , 并求;(2)、求 .
(1)、用向量表示向量 , 并求;(2)、求 . -
3、如图,在三棱锥中,设 , 若 , , 则( )
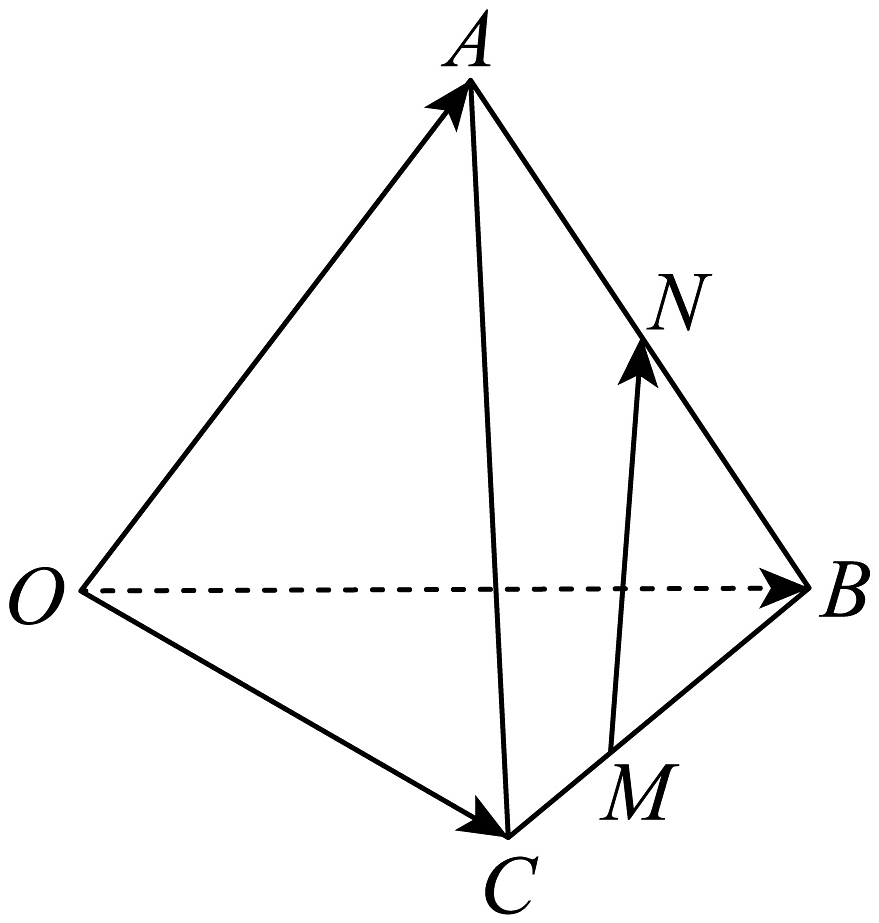 A、 B、 C、 D、
A、 B、 C、 D、 -
4、已知全集 , 集合或.(1)、求;(2)、求.
-
5、已知是二次函数,且满足 , .(1)、求函数的解析式;(2)、设函数 , 求在区间上的最小值的表达式;(3)、在(2)的条件下,对任意的 , 存在 , 使得不等式成立,求的取值范围.
-
6、函数且 过定点 , 则________
-
7、已知函数 , 则下列关于函数的结论错误的是( )A、 B、若 , 则的值是 C、的解集为 D、的值域为
-
8、已知正四棱柱中, , .
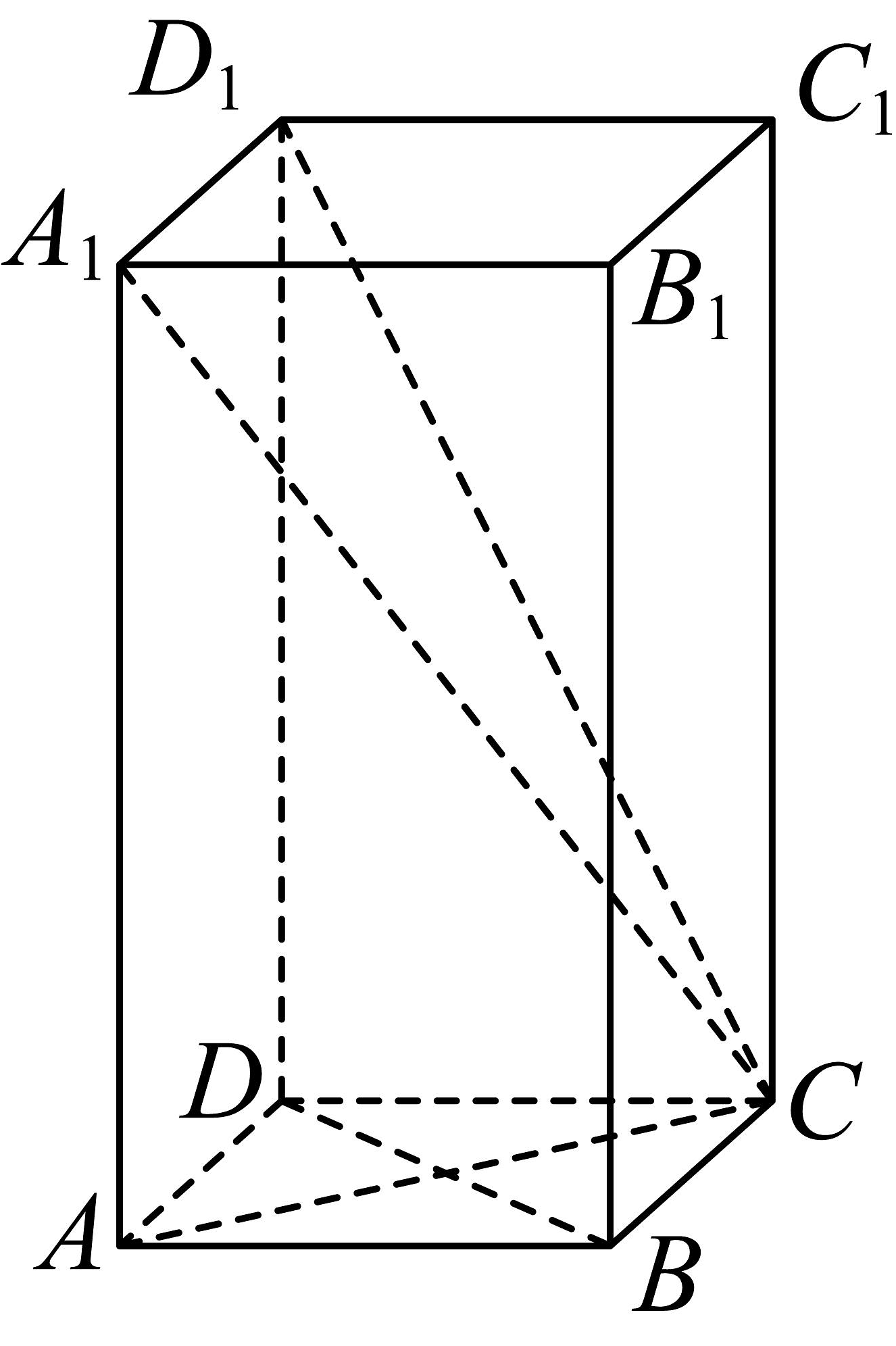 (1)、求异面直线与所成角的余弦值;(2)、求二面角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由.
(1)、求异面直线与所成角的余弦值;(2)、求二面角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由. -
9、如图,在四棱锥中,底面为矩形且 , 侧面底面 , 且侧面是正三角形,、分别是 , 的中点.
 (1)、求证:平面;(2)、求直线与平面所成角的余弦值.
(1)、求证:平面;(2)、求直线与平面所成角的余弦值. -
10、某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在到之间,将测量结果按如下方式分成六组:第1组 , 第2组 , …,第6组 , 如图是按上述分组得到的频率分布直方图,以频率近似概率.

(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
-
11、如图,在底面为菱形的平行六面体中,分别在棱上,且 , 且 .
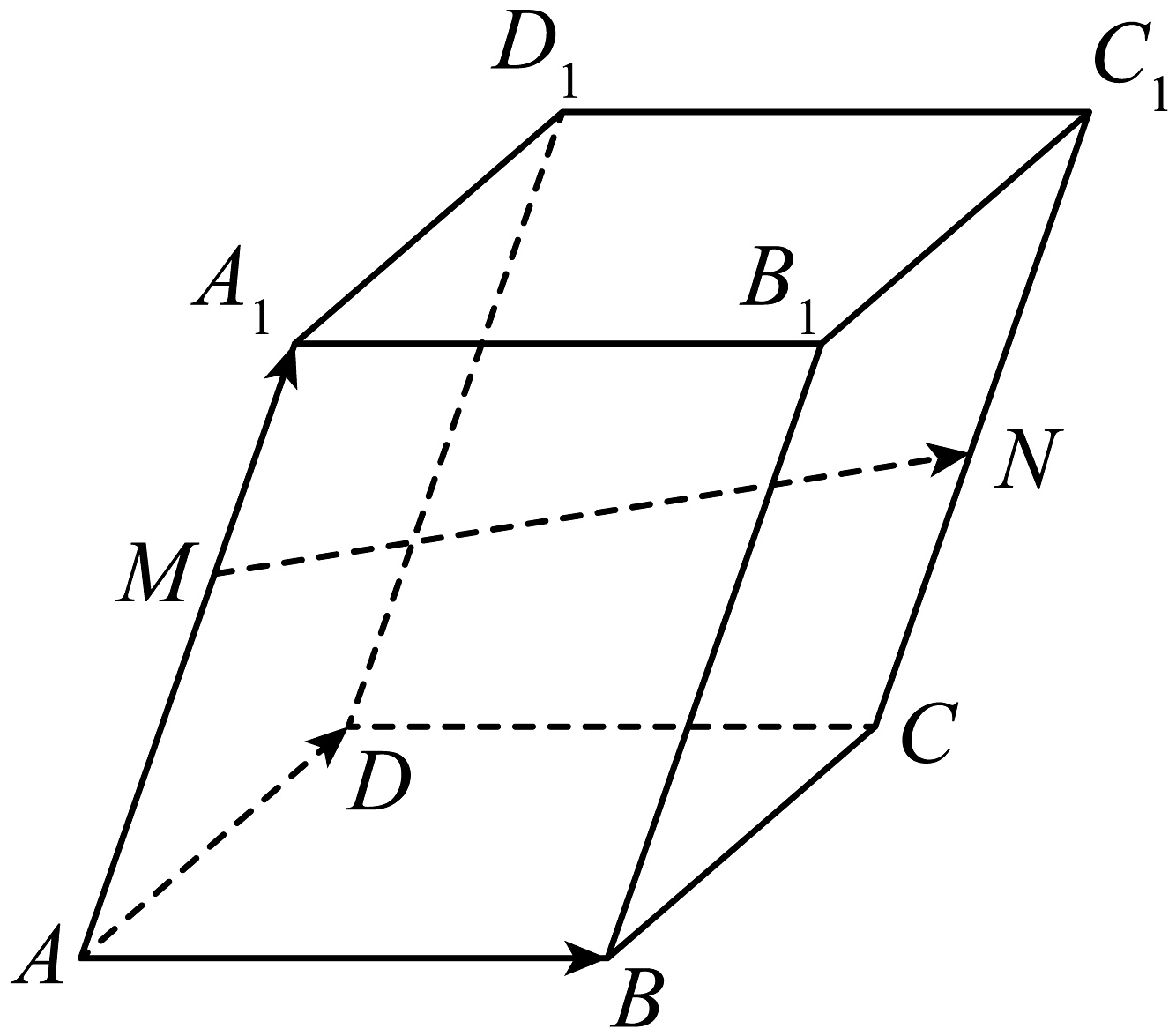 (1)、用向量表示向量;(2)、求证:共面;(3)、当为何值时, .
(1)、用向量表示向量;(2)、求证:共面;(3)、当为何值时, . -
12、某同学参加科普知识竞赛,需回答3个问题,竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分,假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.(1)、求这名同学得200分的概率;(2)、求这名同学至少得300分的概率.
-
13、如图,在直四棱柱中,底面是边长为1的菱形,高为2, , 则点到截面的距离为 .

-
14、直线的倾斜角是直线:的倾斜角的 , 则直线的斜率为.
-
15、已知空间中三点 , , , 则下列说法正确的是( )A、为钝角三角形 B、在上的投影向量为 C、点到直线的距离为 D、的面积为
-
16、设A,B是两个随机事件,已知 , , 则( )A、 B、 C、 D、
-
17、在棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则A、0 B、 C、2 D、
-
18、下列说法正确的是( )A、若直线l1与l2倾斜角相等,则l1∥l2 B、若直线l1⊥l2 , 则k1k2=-1 C、若直线的斜率不存在,则这条直线一定平行于y轴 D、若两条直线的斜率不相等,则两直线不平行
-
19、已知向量 , , 则( )A、50 B、14 C、 D、
-
20、如图所示,在平行六面体中,点满足 , 若 , 则( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,