相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、某日用品按行业质量标准分成五个等级,等级系数依次为1、2、3、4、5,现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
1
2
3
4
5
(1)、若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;(2)、在(1)的条件下,将等级系数为4的3件日用品记为、、 , 等级系数为5的2件日用品记为、 , 现从、、、、这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率. -
2、设函数与均是定义在上的函数,有以下两个命题:①若是周期函数,且是上的减函数,则函数必为常值函数;②若对任意的a, , 有成立,且是上的增函数,则是上的增函数.则以下选项正确的是( )A、①是真命题,②是假命题 B、两个都是真命题 C、①是假命题,②是真命题 D、两个都是假命题
-
3、抛掷三枚硬币,若记“出现三个正面”、“两个正面一个反面”和“两个反面一个正面”分别为事件A、B和C,则下列说法错误的是( )A、事件A、B和C两两互斥 B、 C、事件A与事件是对立事件 D、事件与相互独立
-
4、渐进式延迟退休方案是指采取较缓而稳妥的方式逐步延长退休年龄.对于男职工,新方案将延迟法定退休年龄每4个月延迟1个月,逐步将男职工的法定退休年龄从原六十周岁延迟至六十三周岁.如果男职工延迟法定退休年龄部分对照表如下表所示:
出生时间
1965年
1月-4月
1965年
5月-8月
1965年
9月-12月
1966年
1月-4月
……
改革后法定退休年龄
60岁+1个月
60岁+2个月
60岁+3个月
60岁+4个月
……
那么1974年5月出生的男职工退休年龄为( )
A、62岁3个月 B、62岁4个月 C、62岁5个月 D、63岁 -
5、已知 , 以下四个数中最大的是( )A、b B、 C、 D、
-
6、交通信号灯由红灯、绿灯、黄灯组成.黄灯设置的时长与路口宽度、限定速度、停车距离有关.根据路况不同,道路的限定速度一般在30千米/小时至70千米/小时之间.由相关数据,驾驶员反应距离(单位:米)关于车速v(单位:米/秒)的函数模型为:;刹车距离(单位:米)关于车速v(单位:米/秒)的函数模型为: , 反应距离与刹车距离之和称为停车距离.已知某个十字路口宽度为30米,为保证通行安全,黄灯亮的时间是允许限速车辆离停车线距离小于停车距离的汽车通过十字路口,则该路口黄灯亮的时间最多为秒(结果精确到0.01秒).
-
7、已知平面向量 , 的夹角为 , 与的夹角为 , , 和在上的投影为x,y,则的取值范围是 .
-
8、已知点P为椭圆上任意一点,为圆的任意一条直径,则的取值范围是 .
-
9、已知函数的表达式为 , 则满足的实数m的最大值为 .
-
10、已知等比数列中, , 则 .
-
11、已知 , 则= .
-
12、已知一个圆锥的底面半径为3,其侧面积为 , 则该圆锥的高为 .
-
13、若复数满足(其中是虚数单位),则复数的共轭复数 .
-
14、在中,角、、所对的边分别为、、 , 若 , , , 则.
-
15、函数的定义域是 .
-
16、已知集合 , , 则 .
-
17、已知复数 , 为的共轭复数,则的虚部为( )A、 B、 C、 D、
-
18、在空间直角坐标系中,已知向量 , 点.若直线以为方向向量且经过点 , 则直线的标准式方程可表示为;若平面以为法向量且经过点 , 则平面的点法式方程表示为.(1)、已知直线的标准式方程为 , 平面的点法式方程可表示为 , 求直线与平面所成角的余弦值;(2)、已知平面的点法式方程可表示为 , 平面外一点 , 求点到平面的距离;(3)、(i)若集合 , 记集合中所有点构成的几何体为 , 求几何体的体积:
(ii)若集合.记集合中所有点构成的几何体为 , 求几何体相邻两个面(有公共棱)所成二面角的大小
-
19、如图,在圆上任取一点 , 过点作轴的垂线段 , 为垂足,点在的延长线上,且 , 当点在圆上运动时,记点的轨迹为曲线(当点经过圆与轴的交点时,规定点与点重合).
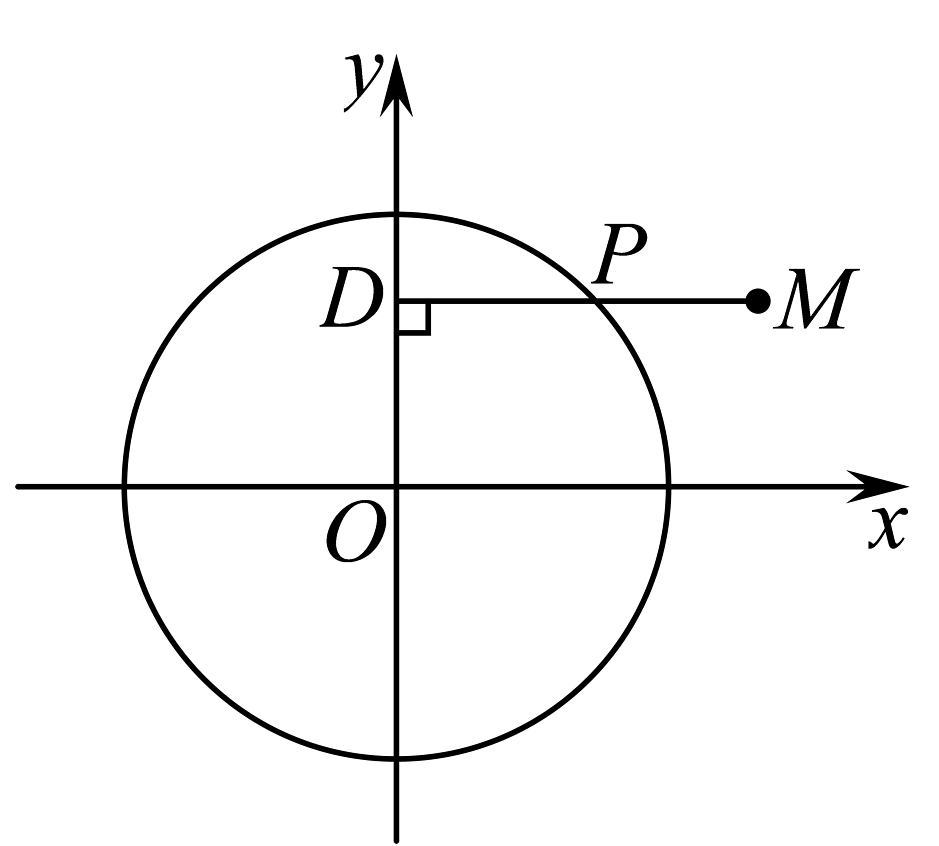 (1)、求曲线的方程;(2)、过点作圆的切线交曲线于两点,将表示成的函数,并求的最大值.
(1)、求曲线的方程;(2)、过点作圆的切线交曲线于两点,将表示成的函数,并求的最大值. -
20、已知线段AB的端点B的坐标是 , 端点A在圆上运动.
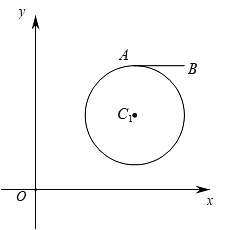 (1)、求线段AB的中点P的轨迹的方程;(2)、设圆与曲线的两交点为M,N,求线段MN的长;(3)、若点C在曲线上运动,点Q在x轴上运动,求的最小值.
(1)、求线段AB的中点P的轨迹的方程;(2)、设圆与曲线的两交点为M,N,求线段MN的长;(3)、若点C在曲线上运动,点Q在x轴上运动,求的最小值.