相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、如图所示,四边形是直角梯形,平面.
 (1)、若M为SC的中点,求证:SBAM(2)、求SC与平面所成角的正弦值;(3)、求平面与平面的夹角的余弦值.
(1)、若M为SC的中点,求证:SBAM(2)、求SC与平面所成角的正弦值;(3)、求平面与平面的夹角的余弦值. -
2、某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为.
 (1)、求频率分布直方图中的值;(2)、估计该企业的职工对该部门评分的75%分位数(结果精确到0.1);(3)、从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
(1)、求频率分布直方图中的值;(2)、估计该企业的职工对该部门评分的75%分位数(结果精确到0.1);(3)、从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率. -
3、已知集合 是集合 的真子集且 , 如果 , 使得 , 其中 , 则称 是集合 的一组有序基底集,记为 .已知 ,且 为 的一组有序基底集,则集合 中的元素之和小于 4 的概率为 .
-
4、如图,在棱长为1的正方体中:直线到平面的距离为.

-
5、已知空间向量和 , 则在上的投影向量为(用坐标表示).
-
6、某高中有学生人,其中男生人,女生人,希望获得全体学生的身高信息,按照分层抽样的原则抽取了容量为的样本.经计算得到男生身高样本均值为 , 方差为;女生身高样本均值为 , 方差为 . 下列说法中正确的是( )A、男生样本量为 B、每个女生入样的概率均为 C、所有样本的均值为 D、所有样本的方差为
-
7、一个装有8个球的口袋中,有标号分别为1,2的2个红球和标号分别为1,2,3,4,5,6的6个蓝球,除颜色和标号外没有其他差异.从中任意摸1个球,设事件“摸出的球是红球”,事件“摸出的球标号为偶数”,事件“摸出的球标号为3的倍数”,则( )A、事件A与事件C互斥 B、事件B与事件C互斥 C、事件A与事件B相互独立 D、事件B与事件C相互独立
-
8、某研究小组依次记录下10天的观测值:26,28,22,24,22,78,32,26,20,22,则( )A、众数是22 B、80百分位数是28 C、平均数是30 D、前4个数据的方差比最后4个数据的方差小
-
9、如图,棱长为3的正方体ABCD-A1B1C1D1中,P为正方体表面BCC1B1上的一个动点,E,F分别为BD1的三等分点,则的最小值为( )
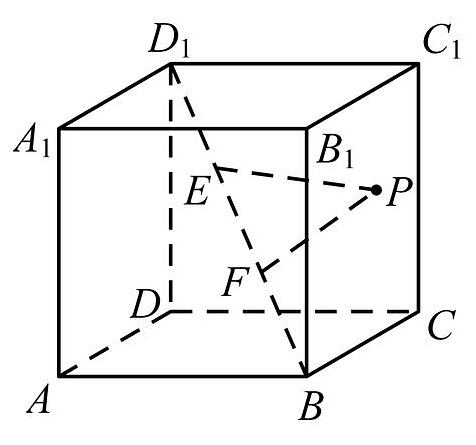 A、 B、 C、 D、
A、 B、 C、 D、 -
10、某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )A、70和50 B、70和67 C、75和50 D、75和67
-
11、已知向量 , 单位向量满足 , 则的夹角为( )A、 B、 C、 D、
-
12、本周末为校友返校日,据气象统计资料,这一天吹南风的概率为 , 下雨的概率为 , 吹南风或下雨的概率为 , 则既吹南风又下雨的概率为( )A、 B、 C、 D、
-
13、下列关于空间向量的命题中,正确的有( )A、直线的方向向量 , 平面的法向量是 , 则 B、若是空间的一组基底,则向量也是空间一组基底 C、若非零向量满足 , 则有 D、若是空间的一组基底,且 , 则四点共面
-
14、一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110
321
230
023
123
021
132
220
001
231
130
133
231
031
320
122
103
233
由此可以估计事件M发生的概率为( )
A、 B、 C、 D、 -
15、已知函数 , 则( )A、在单调递增 B、有两个零点 C、的最小值为 D、在点处切线为
-
16、若、、 , , 则下列不等式中成立的是( )A、 B、 C、 D、
-
17、两条都与轴平行的直线之间的距离为 , 它们与抛物线和圆分别交于点 , 和 , , 则的最大值为.
-
18、圆关于直线对称,则实数( )A、1 B、-3 C、1或-3 D、-1或3
-
19、函数的最小正周期为
-
20、某校为了解学生对安全知识的重视程度,进行了一次安全知识答题比赛.随机抽取的100名学生的笔试成绩(满分200分),分成共五组后,得到的频率分布图表如下所示:
 (1)、求这100名参赛者得分的第85百分位数;(2)、估计这100名学生的成绩的平均数.(3)、为能更好了解学生的知识掌握情况,学校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面答,最终从6位学生中随机抽取2位参加市安全知识答题决赛,求抽到的2位学生不同组的概率.
(1)、求这100名参赛者得分的第85百分位数;(2)、估计这100名学生的成绩的平均数.(3)、为能更好了解学生的知识掌握情况,学校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面答,最终从6位学生中随机抽取2位参加市安全知识答题决赛,求抽到的2位学生不同组的概率.