相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、把化成角度是( )A、 B、 C、 D、
-
2、已知或 , 若集合 , , 则( ).A、 B、 C、 D、
-
3、已知函数在时取得极值,且满足 .(1)、求函数的解析式;(2)、若存在实数 , 使得成立,求整数的最小值.
-
4、《中华人民共和国乡村振兴促进法》中指出:全面实施乡村振兴战略,开展促进乡村产业振兴、人才振兴、文化振兴、生态振兴、组织振兴,推进城乡融合发展,为深入践行习近平总书记提出“绿水青山就是金山银山”的理念,围绕产业发展生态化,生态建设产业化”思路,某乡镇为全力打造成“生态特色小镇”,调研发现:某种农作物的单株产量(单位:)与肥料费用(单位:元)满足如下关系: , 其他总成本为(单位:元),已知这种农作物的市场售价为5元/ , 且供不应求,记该单株农作物获得的利润为(单位:元)(1)、求的函数关系式;(2)、当投入的肥料费用为多少元时,该农作物单株获得的利润最大?最大利润是多少元?
-
5、已知函数.(1)、求函数的最小正周期和单调递增区间;(2)、若在区间上有且只有两个零点,求的取值范围.
-
6、已知 , 则.
-
7、已知函数 , 则.
-
8、下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 则
-
9、若函数定义域为 , 且偶函数,关于点成中心对称,则( )A、56 B、57 C、58 D、59
-
10、函数的部分图象可能是( )A、
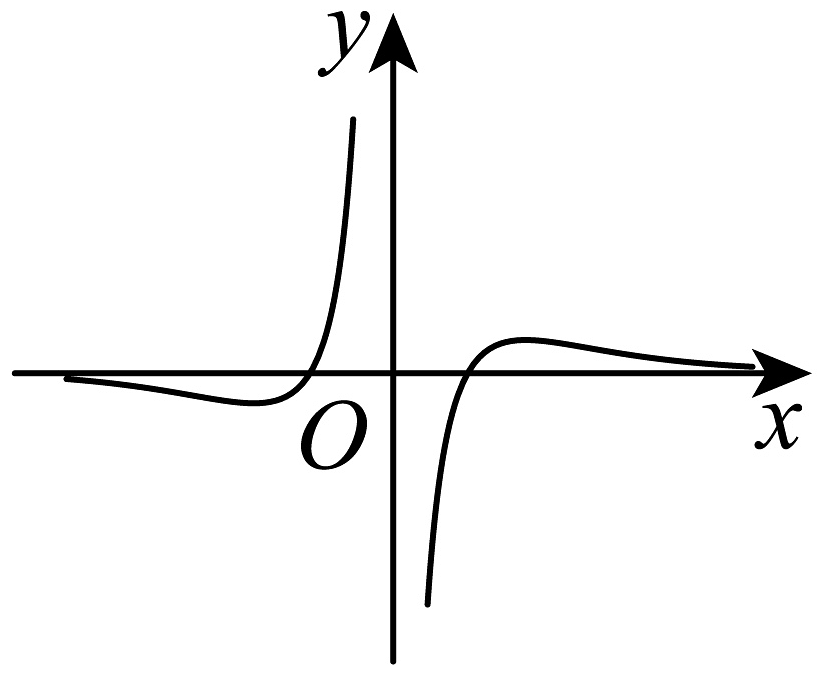 B、
B、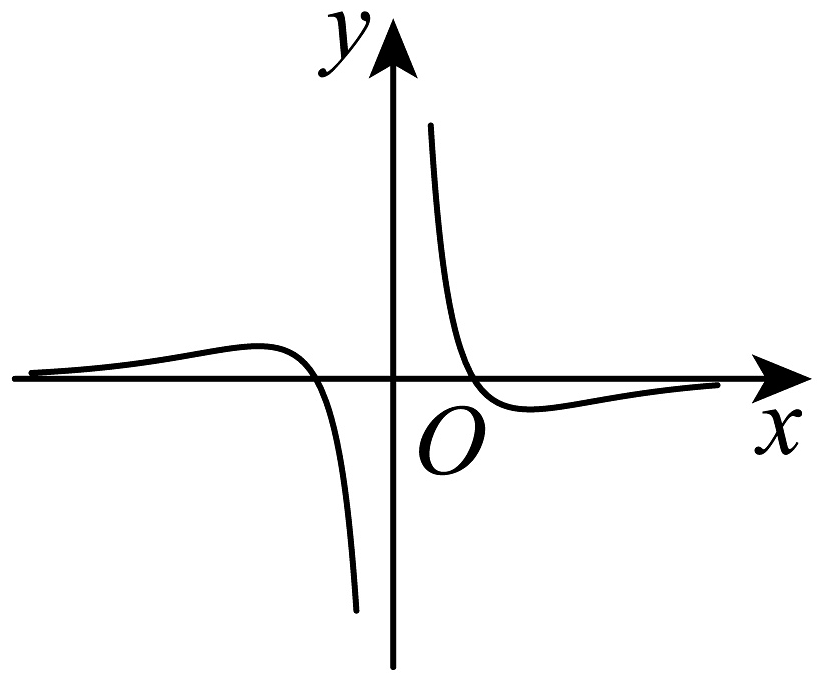 C、
C、 D、
D、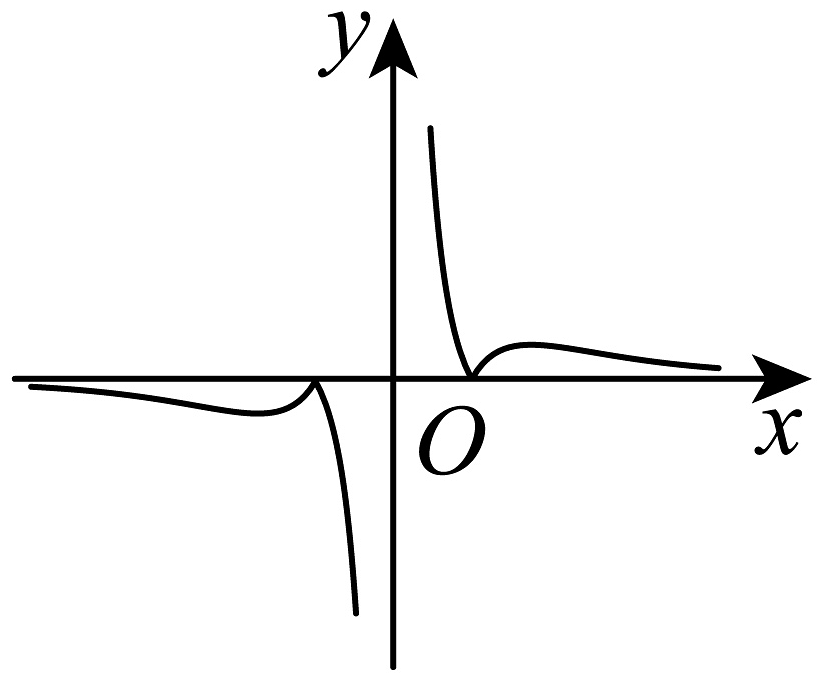
-
11、已知函数 , 则是成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
12、青少年视力问题是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据和小数记录法的数据满足 . 已知小明和小李视力的五分记录法的数据分别为和 , 记小明和小李视力的小数记录法的数据分别为 , 则的值所在区间是( )A、 B、 C、 D、
-
13、设 , , , 则 , , 的大小关系为( )A、 B、 C、 D、
-
14、设 , 函数 , 当时,函数有个零点;若函数恰有3个零点,则实数的取值范围为 .
-
15、对于平面凸四边形 , 若 , 则四边形的面积为( )A、 B、 C、 D、大小不确定
-
16、如图,平面四边形中, , , , , 沿将折起成直二面角(折起后原来平面图形的D点变为空间图形的P点),则折起后四面体的内切球半径为 .
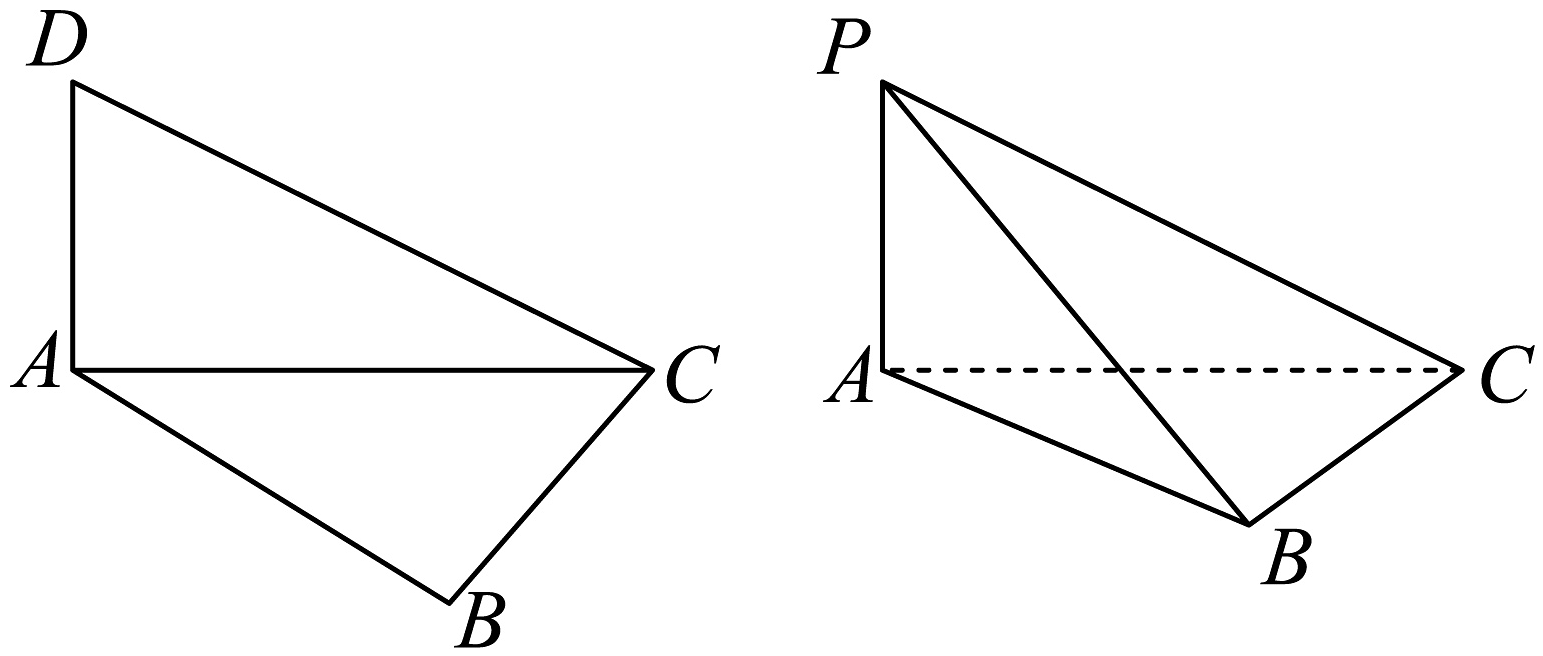
-
17、如图,已知抛物线的焦点为 , 斜率为的直线经过且交于两点(在第一象限).
 (1)、求的坐标与的长;(2)、设 , 如下构造:直线分别与交于 , 证明:
(1)、求的坐标与的长;(2)、设 , 如下构造:直线分别与交于 , 证明:(ⅰ)的纵坐标是等差数列;
(ⅱ).
-
18、在中, , 点D在BC上,满足 , .(1)、若 , 求的面积;(2)、求余弦值的最小值.
-
19、如图,在以为顶点的五面体中,四边形与四边形均为等腰梯形, , .
 (1)、证明:平面平面;(2)、若为线段上一点,且 , 求二面角的余弦值.
(1)、证明:平面平面;(2)、若为线段上一点,且 , 求二面角的余弦值. -
20、如图①,用一个平面去截圆锥,得到的截口曲线是椭圆.许多人从纯几何的角度出发对这个问题进行过研究,其中比利时数学家Germinal dandelin(1794-1847)的方法非常巧妙,极具创造性.在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面,截面相切,两个球分别与截面相切于E,F,在截口曲线上任取一点A,过A作圆锥的母线,分别与两个球相切于C,B,由球和圆的几何性质,可以知道,AE=AC,AF=AB,于是AE+AF=AB+AC=BC.由B,C的产生方法可知,它们之间的距离BC是定值,由椭圆定义可知,截口曲线是以E,F为焦点的椭圆.
如图②,一个半径为2的球放在桌面上,桌面上方有一个点光源P,则球在桌面上的投影是椭圆.已知是椭圆的长轴,垂直于桌面且与球相切, , 则椭圆的离心率为 .

