相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、在中,若动点满足 , 则点的轨迹一定经过的( )A、重心 B、垂心 C、外心 D、内心
-
2、一海轮从A处出发,以每小时40海里的速度沿南偏东的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东 , 在B处观察灯塔,其方向是北偏东 , 那么B,C两点间的距离是( )A、海里 B、海里 C、海里 D、海里
-
3、已知内角A、B、C的对边分别为a、b、c,若的面积为 , 则为( )A、 B、 C、 D、
-
4、已知是不同的直线,是不同的平面,则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
5、如图,已知 , 用表示 , 则等于
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、若复数满足 , 则的虚部为( )A、 B、 C、 D、1
-
7、如图,在直三棱柱中, .
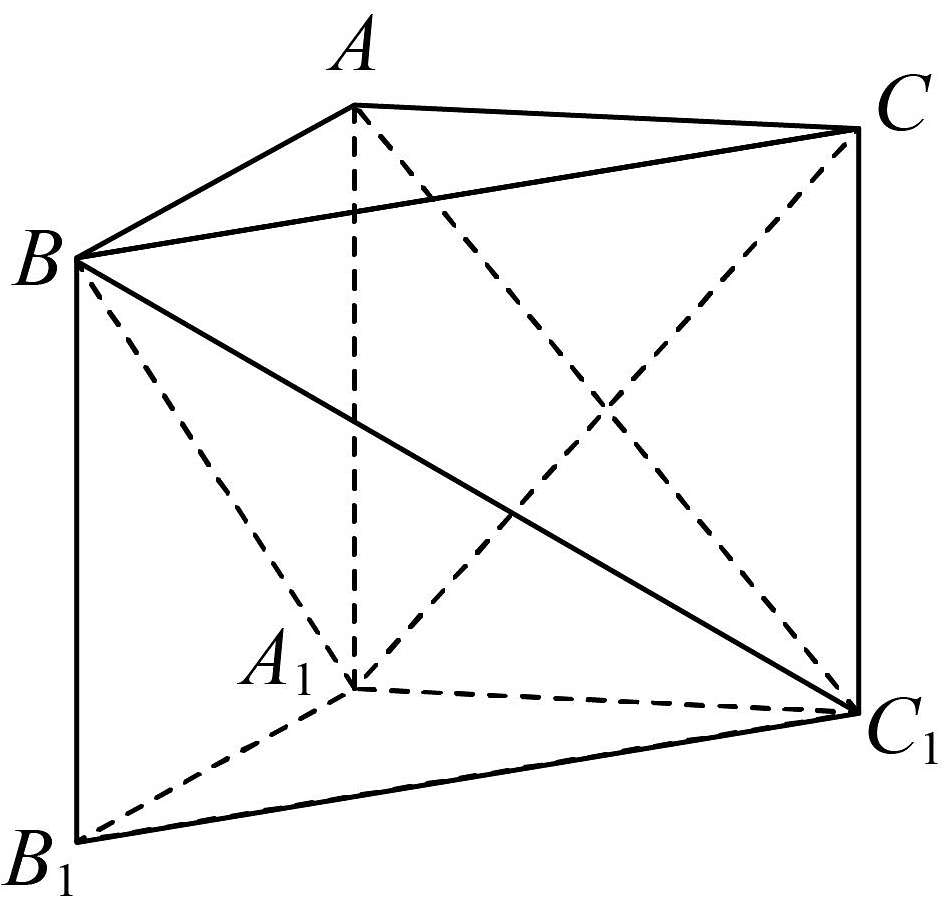 (1)、证明:平面;(2)、求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值. -
8、随着居民家庭收入的不断提高,人们对居住条件的改善的需求也在逐渐升温.某城市统计了最近5个月的房屋交易量,如下表所示:
时间
1
2
3
4
5
交易量(万套)
0.8
1.0
1.2
1.5
若与满足一元线性回归模型,且经验回归方程为 , 则下列说法错误的是( )
A、根据表中数据可知,变量与正相关 B、经验回归方程中 C、可以预测时房屋交易量约为(万套) D、时,残差为 -
9、对于 , 记为关于的“差比模”.若取遍 , 记关于的“差比模”的最大值为 , 最小值为 , 若 , 则称关于的“差比模”是协调的.(1)、若 , 求关于的“差比模”;(2)、若 , 是否存在 , 使得关于的“差比模”是协调的?若存在,求出的值;若不存在,说明理由;(3)、若且 , 若关于的“差比模”是协调的,求的值.
-
10、设椭圆的离心率等于 , 抛物线的焦点是椭圆的一个顶点,分别是椭圆的左右顶点.(1)、求椭圆的方程;(2)、动点、为椭圆上异于的两点,设直线 , 的斜率分别为 , , 且 , 求证:直线经过定点.
-
11、某大学有甲、乙两个运动场.假设同学们可以任意选择其中一个运动场锻炼,也可选择不锻炼,一天最多锻炼一次,一次只能选择一个运动场.若同学们每次锻炼选择去甲或乙运动场的概率均为 , 每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为 , 已知的分布列如下:(其中)
0
1
2
3
(1)、记事件表示王同学假期三天内去运动场锻炼次 , 事件表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当时,试根据全概率公式求的值;(2)、是否存在实数 , 使得?若存在,求的值:若不存在,请说明理由;(3)、记表示事件“甲运动场举办锻炼有奖的抽奖活动”,表示事件“王同学去甲运动场锻炼”,.已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明:. -
12、已知抛物线 , 点在抛物线上,且在轴上方,和在轴下方(在左侧),关于轴对称,直线交轴于点 , 延长线段交轴于点 , 连接.(1)、证明:为定值(为坐标原点);(2)、若点的横坐标为 , 且 , 求的内切圆的方程.
-
13、已知函数 , 且曲线在点处的切线方程为 .(1)、求实数 , 的值;(2)、证明:函数有两个零点.
-
14、在三棱锥中,平面平面 , , , 分别为的中点.
 (1)、证明:平面;(2)、求二面角的正弦值.
(1)、证明:平面;(2)、求二面角的正弦值. -
15、在中,角的对边分别是 , 且.(1)、求的值;(2)、若的面积为 , 求的周长.
-
16、已知四棱锥的底面为矩形, , , 侧面为正三角形且垂直于底面 , 为四棱锥内切球表面上一点,则点到直线距离的最小值为.
-
17、现安排甲、乙、丁、丙、戊五位老师从周一到周五的常规值班,每人一天,每天一人,则甲、乙两人相邻,丙不排在周三的概率为.
-
18、已知定义在上的函数满足: , 都有 , 且 , , 当时,有 , 则( )A、 B、 C、 D、
-
19、下列说法中,正确的是( )A、若随机变量 , 且 , 则 B、一组数据6,7,7,9,13,14,16,17,21的第70百分位数为16 C、盒子中装有除颜色外完全相同的5个黄球和3个蓝球,从袋中有放回地依次抽取2个球,第一次抽到蓝球的情况下第二次也抽到蓝球的概率为 D、设随机事件 , , 已知事件发生的概率为0.3,在发生的条件下发生的概率为0.4,在不发生的条件下发生的概率为0.2,则发生的概率为0.26
-
20、已知双曲线:的左右焦点分别为 , 过点作直线交双曲线右支于两点(点在轴上方),使得.若 , 则双曲线的离心率为( )A、 B、 C、 D、2