相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、如图,在直三棱柱中,底面是等腰直角三角形, , 侧棱 , D、E分别是与的中点,点E在平面ABD上的射影是的重心.
(Ⅰ)求与平面ABD所成角的余弦值
(Ⅱ)求点到平面的距离

-
2、记锐角的内角A、B、C的对边分别为a,b,c,已知.(1)、求的值.(2)、若 , 求边上的高的取值范围.
-
3、已知设P:函数在R上单调递减.Q:不等式的解集为R,如果P和Q有且仅有一个正确,则的取值范围为.
-
4、展开式中的系数是
-
5、函数 , 向右平移3个单位得到 , 下列说法正确的是( )A、的极小值点为 B、当有两解时, C、若 , , 则 D、若 , 那么 , 且有且仅有一解
-
6、如图所示,在四个正方体中,是正方体的一条体对角线,点分别为其所在棱的中点,能得出平面的图形为( )A、
 B、
B、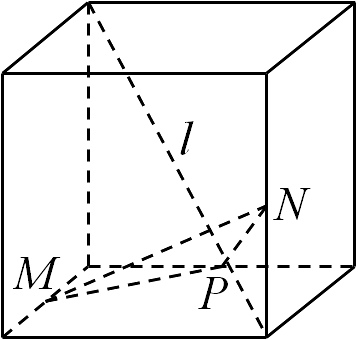 C、
C、 D、
D、
-
7、我们知道一元二次方程可以变形为 , 展开后对应项易得到韦达定理,那么类比推理过程,在一个一元三次方程 , 则下列关于此一元三次方程的根的式子正确的是( )A、++=2 B、++= C、= D、++=7
-
8、已 知长方形的四个顶点.一质点从的中点沿与夹角为的方向射到上的点后,依次反射到上的点 (入射角等于反射角).设的坐标为.若 , 则的取值范围是( ).A、 B、 C、 D、
-
9、下列说法正确的个数为( )
①180的正因数有16个②以正方体为顶点的三棱锥有70个③+9能被7整除
④投一枚质地均匀的硬币十次,正面朝上频率在 的概率为
A、1个 B、2个 C、3个 D、4个 -
10、若方程的四个根组成一个首项为的等差数列,则( )A、1 B、 C、 D、
-
11、已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )A、 B、 C、 D、
-
12、存在狄利克雷函数 , 若 , , 则的所有值之和为( )A、3 B、6 C、12 D、13
-
13、双曲线两个焦点 , 焦距为8,M为曲线上一点,则( )A、1 B、1或9 C、9 D、3
-
14、已知空间中向量=(0,1,0),向量的单位向量为(),则点B到直线AC的距离为( )A、 B、 C、 D、
-
15、已知函数 .(1)、求函数的最小正周期及对称轴;(2)、在锐角中,设角A,B,C所对的边分别是a,b,c,若且 , 求的取值范围.
-
16、如图,在四边形中,为等边三角形,是边上靠近的三等分点.设.
 (1)、用表示;(2)、求的余弦值.
(1)、用表示;(2)、求的余弦值. -
17、已知向量 , 若 ,(1)、求与的夹角θ;(2)、求;(3)、当λ为何值时,向量与向量互相垂直?
-
18、函数在上恰有个零点,则的取值范围是 .
-
19、如图,在矩形ABCD中,AB= , BC=2,点E为BC的中点,点F在边CD上,若= , 则的值是 .

-
20、如图是四边形ABCD的水平放置的直观图A'B'C'D' , 则原四边形ABCD的面积是 .
