相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知定义域是的函数不恒为0,满足 , 且则( )A、 B、 C、是函数的一条对称轴 D、
-
2、已知 , 为椭圆的右顶点和上顶点, , 为椭圆的左、右焦点,为椭圆上一点,圆的圆心在第一象限,且与轴相切于点 , 直线与圆的另一个交点为 , 直线(为坐标原点)垂直于直线 , 记椭圆的离心率为 , 则( )A、若且 , 则 B、若 , 则最大值为 C、是圆的切线 D、若为线段的中点,则
-
3、随机变量 , 且 , 则( )A、 B、 C、 D、
-
4、已知函数(且)在上有唯一零点,则的范围为( )A、 B、 C、 D、
-
5、甲乙两人玩跳棋游戏,约定由抛两次硬币的结果确定谁先走,若两次都正面向上,则甲先走,否则乙先走,已知甲先走的情况下,甲胜的概率为 , 乙先走的情况下,甲胜的概率为 , 则甲获胜的概率是( )A、 B、 C、 D、
-
6、函数的部分图象是( )A、
 B、
B、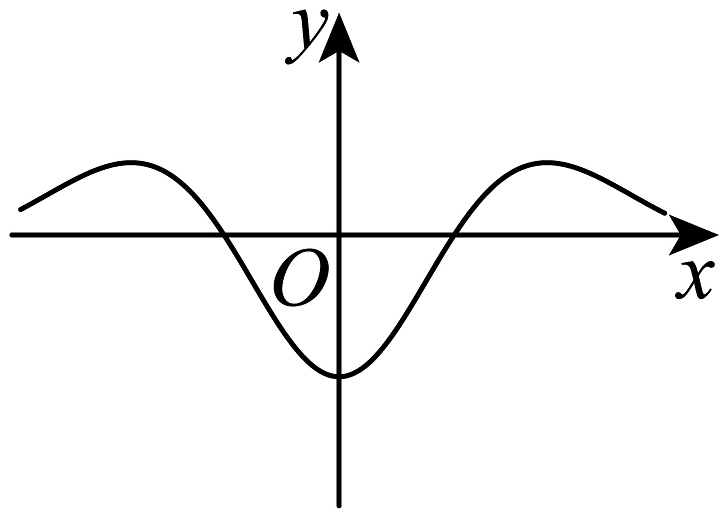 C、
C、 D、
D、
-
7、已知向量与向量垂直,则( )A、1 B、 C、 D、2
-
8、以边长为1的正方形的一条边所在的直线为轴旋转一周,得到的几何体的体积为( )A、 B、 C、 D、
-
9、命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,
-
10、设 , 则( )A、 B、 C、 D、
-
11、已知集合 , , 则( )A、 B、 C、 D、
-
12、记的内角A,B,C的对边分别为a,b,c,已知 .(1)、求的值;(2)、若 , 求的最大值.
-
13、已知 , ,
(1)求的最小正周期及单调递减区间;
(2)已知锐角的内角的对边分别为 , 且 , , 求边上的高的最大值.
-
14、某企业要设计一款由同底等高的圆柱和圆锥组成的油罐(如图),设计要求:圆锥和圆柱的总高度与圆柱的底面半径相等,均为10m.
 (1)、已知制作这种油罐的材料单价为1.5万元/m2 , 则制作一个油罐所需费用为多少万元?(2)、已知该油罐的储油量为0.95吨/m3 , 则一个油罐可储存多少吨油?
(1)、已知制作这种油罐的材料单价为1.5万元/m2 , 则制作一个油罐所需费用为多少万元?(2)、已知该油罐的储油量为0.95吨/m3 , 则一个油罐可储存多少吨油? -
15、如图,长方体的体积是120,E为的中点,则三棱锥E-BCD的体积是.

-
16、已知为单位向量, , 向量 , 的夹角为 , 则在上的投影向量是.
-
17、在中,内角所对的边分别为 , 则下列说法正确的是( )A、 B、若 , 且 , 则为等边三角形 C、若 , 则是等腰三角形 D、在中, , 则使有两解的的范围是
-
18、先将函数的图像向右平移个单位长度后,再将横坐标缩短为原来的 , 得到函数的图像,则关于函数 , 下列说法正确的是( )A、在上单调递增 B、图像关于直线对称 C、在上单调递减 D、最小正周期为π,图像关于点对称
-
19、已知i为虚数单位,则下列结论正确的是( )A、复数的虚部为 B、复数在复平面内对应的点位于第四象限 C、若 , 则 D、若复数z满足 , 则
-
20、已知正三棱锥P-ABC的底面边长为6,顶点P到底面ABC的距离是 , 则这个正三棱锥的侧面积为( )A、27 B、 C、9 D、