相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知 , 且 , 则( )A、 B、 C、 D、
-
2、已知空间向量满足 , 则( )A、 B、1 C、0 D、
-
3、函数的最小正周期为( )A、 B、 C、 D、
-
4、把函数的图象按向量平移,得到的图象,则( )A、 B、 C、 D、
-
5、若集合 , 则( )A、 B、 C、 D、
-
6、牛顿法是17世纪牛顿在《流数法与无穷级数》一书中,给出了高次代数方程的一种数值解法.具体步骤如下:设是函数的一个零点,任取作为的初始近似值,过点作曲线的切线 , 设与轴交点的横坐标为 , 并称为的1次近似值;过点作曲线的切线 , 设与轴交点的横坐标为 , 称为的2次近似值;一直继续下去,得到.一般地,过点作曲线的切线 , 记与轴交点的横坐标为 , 并称为的次近似值,称数列为牛顿数列.(1)、若函数的零点为.求的2次近似值;(2)、设是函数的两个零点,数列为函数的牛顿数列,数列满足.
(i)求证:数列为等比数列;
(ii)证明:.
-
7、已知分别为椭圆的左,右焦点,为的上顶点,点为椭圆上的一个动点,且三角形面积的最大值为1,焦距为2.
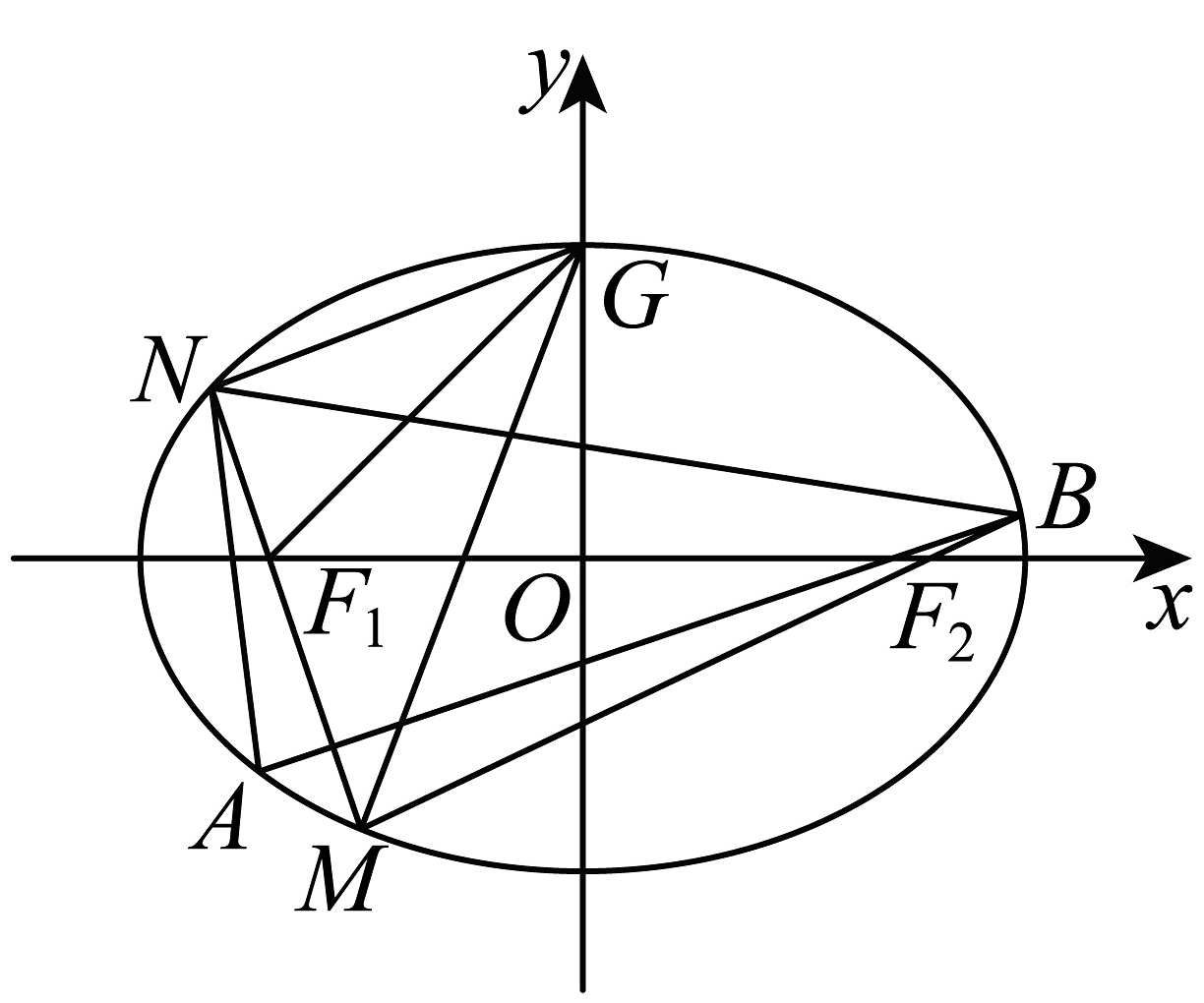 (1)、求椭圆的标准方程;(2)、如图,过点作两直线分别与椭圆相交于点和点.
(1)、求椭圆的标准方程;(2)、如图,过点作两直线分别与椭圆相交于点和点.(i)若点不在坐标轴上,且 , 求直线的方程;
(ii)若直线斜率都存在,且 , 求四边形面积的最小值.
-
8、某系统配置有个元件(为正整数),每个元件正常工作的概率都是 , 且各元件是否正常工作相互独立.如果该系统中有一半以上的元件正常工作,系统就能正常工作.现将系统正常工作的概率称为系统的可靠性.(1)、当时,求该系统正常工作的概率;(2)、现在为了改善原系统的性能,在原有系统中增加两个元件,试问增加两个元件后的新系统的可靠性是提高了,还是降低了?请给出你的结论,并说明理由.
-
9、如图,在三棱柱中,平面平面 , , , , , 为线段上一点,且.
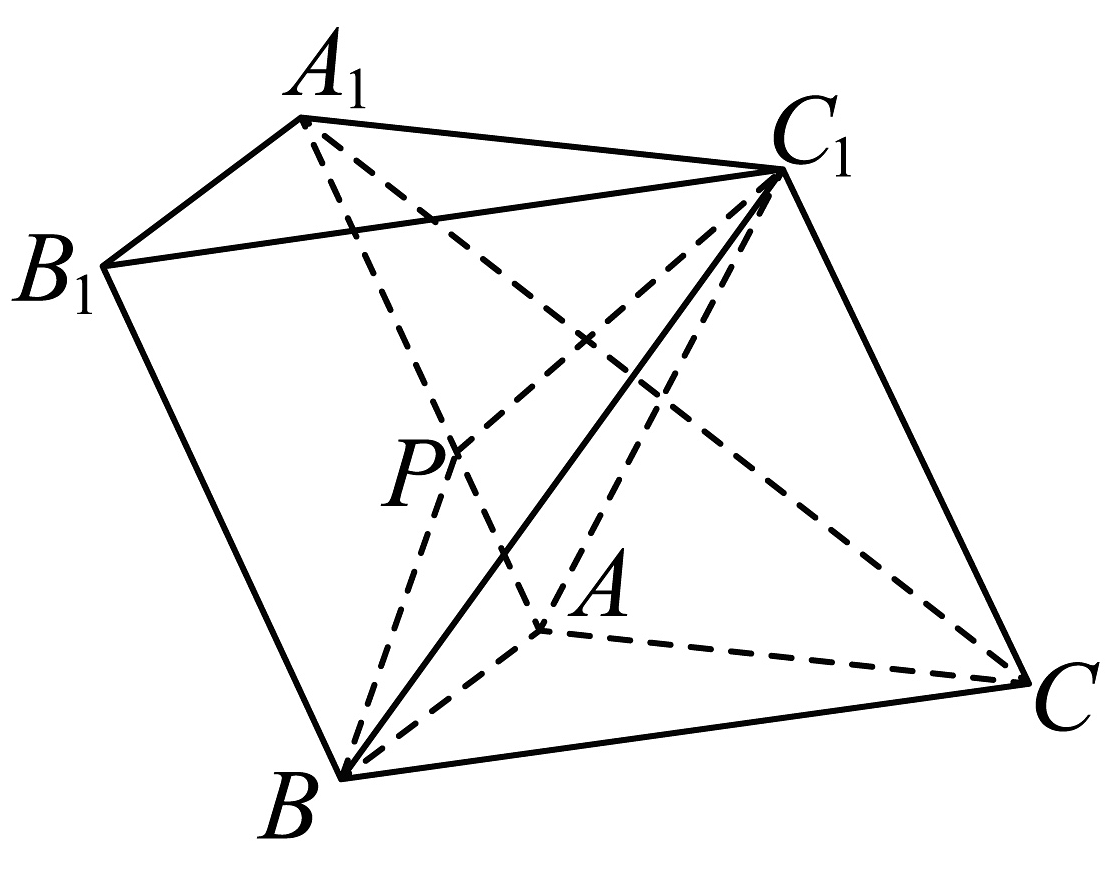 (1)、求证:;(2)、是否存在实数 , 使得平面与平面的夹角余弦值为?若存在,求出实数的值;若不存在,请说明理由.
(1)、求证:;(2)、是否存在实数 , 使得平面与平面的夹角余弦值为?若存在,求出实数的值;若不存在,请说明理由. -
10、已知正项数列的前项和为 , 且.(1)、求数列的通项公式;(2)、设 , 求数列前项的和.
-
11、已知是双曲线的左,右焦点,过左焦点的直线交双曲线左支于两点(其中在轴上方,在轴下方),的内切圆半径为的内切圆半径为.若 , 则直线的斜率等于.
-
12、在中,内角的对边分别是 , 满足.若 , 则的面积的最大值是.
-
13、已知随机变量服从正态分布 , 且 , 则.
-
14、平面直角坐标系中,定义为两点 , 的“切比雪夫距离”;又设点及直线上任意一点 , 称的最小值为点到直线的“切比雪夫距离”,记作.则下列结论正确的是( )A、当时, B、当时, C、对任意三点恒成立 D、动点与定点满足的轨迹围成的面积是16
-
15、如图所示,在平面直角坐标系中,以轴非负半轴为始边的锐角与钝角的终边与单位圆分别交于两点.若点的横坐标为 , 点的纵坐标为 , 则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、每年4月23日为“世界读书日”,某学校于四月份开展“书香润泽校园,阅读提升思想”主题活动,为检验活动效果,学校收集当年二至六月的借阅数据如下表:
二月
三月
四月
五月
六月
月份代码
1
2
3
4
5
月借阅量(百册)
4.9
5.1
5.5
5.7
5.8
根据上表,可得关于的经验回归方程为 , 则下列结论正确的是( )
A、 B、借阅量的下四分位数为5.7 C、与的线性相关系数 D、七月的借阅量一定不少于百册 -
17、已知函数及其导函数的定义域均为 , 记 , 若为偶函数,为奇函数,则下列结论一定正确的是( )A、 B、为偶函数 C、 D、
-
18、已知函数 , 若存在常数 , 使得恒成立,则实数的最小值是( )A、 B、 C、 D、
-
19、圆台的上、下底面的面积分别是 , , 侧面积是 , 则这个圆台的体积是( )A、 B、 C、 D、
-
20、复数(为虚数单位,)在复平面上对应的点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限