相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知数列满足(e为自然对数的底),且.(1)、当时,令 , 求的通项公式及其前n项和;(2)、当时,令 , , , 求的值.
-
2、如图,在直四棱柱中, , , , , 点和分别在侧棱、上,且 .
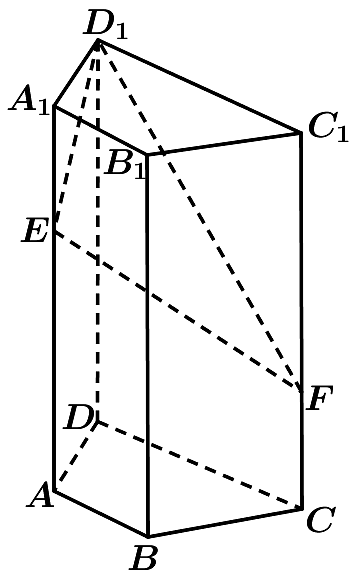
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
-
3、已知锐角中,角A,B,C所对应的边分别为a,b,c,且满足.(1)、求c的值;(2)、若 , 求的值.
-
4、在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若 , 则=.
-
5、已知 , 则 .
-
6、甲、乙两个不透明的袋子中分别装有两种颜色不同但是大小相同的小球,甲袋中装有5个红球和5个绿球;乙袋中装有4个红球和6个绿球.先从甲袋中随机摸出一个小球放入乙袋中,再从乙袋中随机摸出一个小球,记表示事件“从甲袋摸出的是红球”,表示事件“从甲袋摸出的是绿球”,记表示事件“从乙袋摸出的是红球”,表示事件“从乙袋摸出的是绿球”.下列说法正确的是( )A、 , 是互斥事件 B、 , 是独立事件 C、 D、
-
7、以下四个正方体中,满足平面CDE的有( )A、
 B、
B、 C、
C、 D、
D、
-
8、在中, , 且 , 则的值不可以是( )A、 B、 C、1 D、2
-
9、在空间四边形ABCD中, , 三棱锥的体积的最大值等于( )A、2 B、 C、1 D、
-
10、下列选项中的圆既与轴相切又与直线相切的是( )A、 B、 C、 D、
-
11、下表为国家统计局统计的2014年~2023年我国各级各类学校教职工数的统计数据:
2014年
2015年
2016年
2017年
2018年
2019年
2020年
2021年
2022年
2023年
高等学校教职工数(万人)
234
237
240
244
249
257
267
275
284
292
高中阶段教职工数(万人)
365
365
368
375
381
391
403
395
407
418
初中阶段教职工数(万人)
396
398
400
408
420
435
450
469
475
482
小学阶段教职工数(万人)
549
549
554
565
573
585
597
622
625
626
则在这10年的时间里,教职工数的增长率(增长率×100%)最高的是( )
A、高等学校 B、高中阶段 C、初中阶段 D、小学阶段 -
12、已知 , (i为虚数单位),则( )A、 B、4 C、 D、2
-
13、命题p: , 都有 , 则命题的否定是( )A、 , 使得 B、 , 使得 C、 , 使得 D、 , 使得
-
14、已知集合 , , 则( )A、 B、 C、 D、
-
15、 已知函数的定义域为 . 对于正实数a , 定义集合 .(1)、若 , 判断是否是中的元素,请说明理由;(2)、若 , 求a的取值范围;(3)、若是偶函数,当时, , 且对任意 , 均有 . 写出 , 解析式,并证明:对任意实数c , 函数在上至多有9个零点.
-
16、 已知椭圆 , , A是的右顶点.(1)、若的焦点 , 求离心率e;(2)、若 , 且上存在一点P , 满足 , 求m;(3)、已知AM的中垂线l的斜率为2,l与交于C、D两点,为钝角,求a的取值范围.
-
17、 已知 .(1)、若 , 求不等式的解集;(2)、若函数满足在上存在极大值,求m的取值范围;
-
18、 如图,P是圆锥的顶点,O是底面圆心,AB是底面直径,且 .
 (1)、若直线PA与圆锥底面的所成角为 , 求圆锥的侧面积;(2)、已知Q是母线PA的中点,点C、D在底面圆周上,且弧AC的长为 , . 设点M在线段OC上,证明:直线平面PBD .
(1)、若直线PA与圆锥底面的所成角为 , 求圆锥的侧面积;(2)、已知Q是母线PA的中点,点C、D在底面圆周上,且弧AC的长为 , . 设点M在线段OC上,证明:直线平面PBD . -
19、2024年东京奥运会,中国获得了男子米混合泳接力金牌.以下是历届奥运会男子米混合泳接力项目冠军成绩记录(单位:秒),数据按照升序排列.
206.78
207.46
207.95
209.34
209.35
210.68
213.73
214.84
216.93
216.93
(1)、求这组数据的极差与中位数;(2)、从这10个数据中任选3个,求恰有2个数据在211以上的概率;(3)、若比赛成绩y关于年份x的回归方程为 , 年份x的平均数为2006,预测2028年冠军队的成绩(精确到0.01秒). -
20、 已知数列、、的通项公式分别为 , 、,.若对任意的 , 、、的值均能构成三角形,则满足条件的正整数有( )A、4个 B、3个 C、1个 D、无数个