相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知向量 , , 则在上的投影向量的模为( )A、 B、1 C、 D、2
-
2、( ).A、 B、 C、 D、
-
3、如图,是圆柱上底面圆周上的三个不同的点,为直径, , 均为该圆柱的母线.
 (1)、证明:平面平面 .(2)、若 , , , 求与平面所成角的正弦值.
(1)、证明:平面平面 .(2)、若 , , , 求与平面所成角的正弦值. -
4、在”五四”来临之际,某学校团委组织以“春风吹,青春启航”为主题的知识竞赛,比赛分初赛和决赛两个阶段,甲、乙两人进入决赛争夺冠军,决赛规则如下:每轮答题获得分,其概率为 , 获得分,其概率为.最多进行轮答题,某同学累计得分为分时,比赛结束,该同学获得冠军,另一同学获得亚军.(1)、当进行完轮答题后,甲同学总分为 , 求的分布列及;(2)、若累计得分为的概率为 , (初始得分为分,)
①求的表达式().
②求获得亚军的概率.
-
5、在平面直角坐标系xOy中,双曲线 , 离心率为 , 点P是上任意一点.抛物线 ,
 (1)、求的方程;(2)、过点P作的两条渐近线的平行线,分别与两条渐近线交于两点,求证:平行四边形PAOB的面积为定值;(3)、是的两条切线,是切点,求面积的最小值.
(1)、求的方程;(2)、过点P作的两条渐近线的平行线,分别与两条渐近线交于两点,求证:平行四边形PAOB的面积为定值;(3)、是的两条切线,是切点,求面积的最小值. -
6、若函数与函数的图象在公共点处有相同的切线.(1)、当时,求函数与在公共点处的切线方程;(2)、求的最小值:
-
7、在四棱锥中,底面是等腰梯形, , 面底面 .
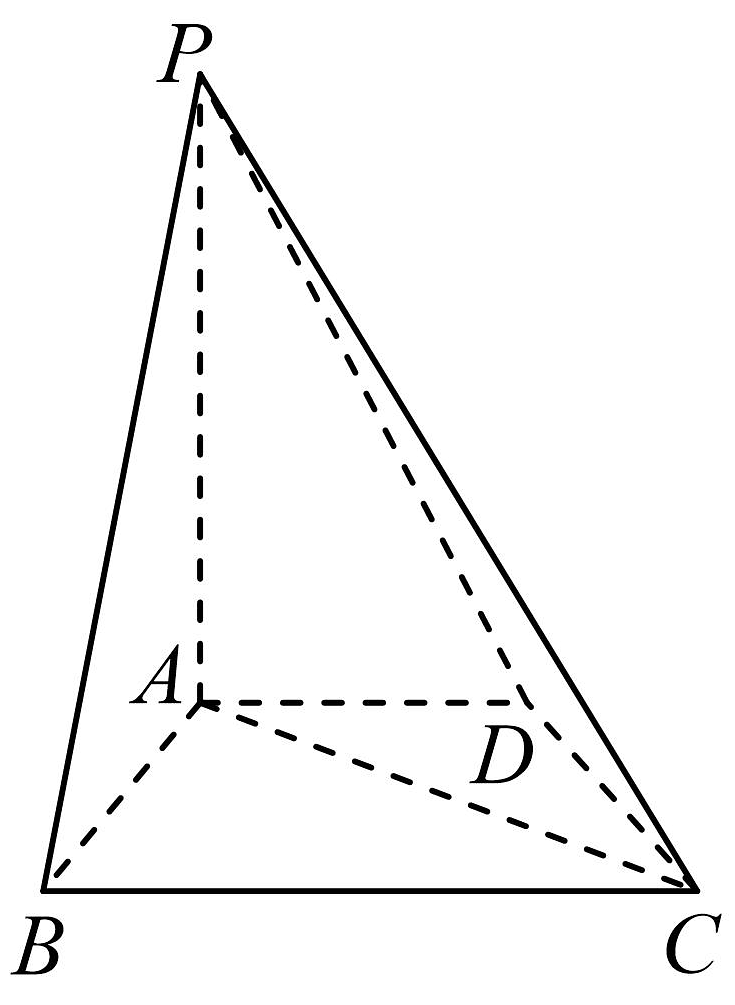 (1)、证明:;(2)、求平面与平面夹角的余弦值.
(1)、证明:;(2)、求平面与平面夹角的余弦值. -
8、已知的三边所对的角分别为 .(1)、求证:;(2)、若 , 求的取值范围.
-
9、如图,将边长为1的正五边形的各边延长,得到一个正五角星.若点在正五角星的内部(含边界),则的最小值为.

-
10、从公比不为1的正项等比数列的前8项中任取三项,则这3项能构成等比数列的概率为 .
-
11、已知 , , 满足 , 则下列说法正确的是( )A、 B、 C、 D、
-
12、已知一几何体上半部分为圆台 , 下半部分为圆锥 , 其中圆锥底面的半径为 , 高为 . 圆台的两底面的半径分别为和 , 高为 . 该几何体内接于表面积为的球,则圆台的体积为( )A、 B、 C、 D、
-
13、已知椭圆 , 称点和直线是椭圆的一对极点和极线,每一对极点与极线是一一对应关系当在圆外时,其极线是椭圆从点所引两条切线的切点所确定的直线(即切点弦所在直线)结合阅读材料回答下面的问题:已知是直线上的一个动点,过点向椭圆引两条切线,切点分别为 , 直线恒过定点 , 当时,直线的方程为( )A、 B、 C、 D、
-
14、已知 , 则的值为( )A、 B、 C、 D、
-
15、在复平面内,复数(i为虚数单位)与点对应,则( )A、 B、 C、 D、
-
16、在公差不为的等差数列中,若 , 则的最小值为( )A、 B、 C、 D、
-
17、已知复数的共轭复数为 , 则( )A、3 B、4 C、5 D、6
-
18、设集合 , , 则( )A、 B、 C、 D、
-
19、已知数列满足 , .(1)、求证:数列是等差数列,并求数列的通项公式:(2)、记 , 求数列的前n项和.
-
20、对于一个函数和两个点 , , 给出如下定义:记: , 若满足 , 则称P是M,N视角下的“基于的回点”.(1)、若 , 点 , , 求:M,N视角下的基于的回点P的坐标;(2)、若 , , 对于点 , , 若M,N视角下的“基于的回点”恰有两个,记为 , , 求证:直线 , 的斜率.