相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知函数.(1)、求曲线在点处的切线方程;(2)、设 , 求证:是上的单调递减函数;(3)、求证:当时,.
-
2、已知椭圆:的一个顶点为 , 离心率为.(1)、求的方程和短轴长;(2)、直线:与E相交于不同的两点B,C,直线 , 分别与直线交于点M,N.当时,求的值.
-
3、AI智能阅卷是一种利用人工智能技术对试卷进行批改和评估的技米,它可以帮助教师提高阅卷效率,并为学生提供更快速更有针对性的反馈.某教师尝试使用AI系统进行阅卷,由甲、乙两种系统进行独立阅卷评分.如果两个系统评分相差2分及以下,则以两种系统评分的平均分作为最后得分;如果两个系统评分相差3分及以上,则人工进行复核阅卷并给出最后得分.从两种系统进行阅卷的试卷中随机抽取12份试卷作为样本,其评分情况如下表所示:
试卷序号
1
2
3
4
5
6
7
8
9
10
11
12
系统甲评分
82
88
76
92
87
66
75
69
90
58
86
84
系统乙评分
80
82
76
90
80
61
71
65
88
54
82
80
最后得分
81
85
76
91
85
64
74
67
89
56
84
83
(1)、从这12份试卷中随机选取1份,求甲、乙两种系统评分之差的绝对值不超过2分的概率;(2)、从这12份试卷中随机选取3份,甲、乙两种系统评分之差的绝对值不超过2分的份数记为X,求X的分布列和数学期望;(3)、从上述的12份试卷中随机抽取1份,设甲系统对其评分为 , 乙系统对其评分为 , 最后得分为.令 , , 试比较方差和的大小.(结论不要求证明) -
4、已知函数.(1)、求的值;(2)、再从条件①、条件②、条件③中选择两个作为已知条件,使函数存在且唯一确定.当在区间上仅有一个零点时,求的取值范围.
条件①:在上是单调函数;
条件②:图象的一个对称中心为;
条件③:对任意的 , 都有成立.
注:如果选择的条件不符合要求,得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
-
5、如图,在四棱锥中,底面是菱形, , , .
 (1)、若平面与棱交于点 , 且平面 , 求证:是中点;(2)、若是棱上一点,且满足 , 当时,求与平面所成角的正弦值.
(1)、若平面与棱交于点 , 且平面 , 求证:是中点;(2)、若是棱上一点,且满足 , 当时,求与平面所成角的正弦值. -
6、已知函数 , 数列满足 , .
给出下列四个结论:
①若 , 则有3个不同的可能取值;
②若 , 则;
③对于任意 , 存在正整数 , 使得;
④对于任意大于2的正整数 , 存在 , 使得;
其中所有正确结论的序号是.
-
7、在中, , , 则.
-
8、已知直线:与圆:有两个交点,则可以是.(写出满足条件的一个值即可)
-
9、若 , 则;.
-
10、已知双曲线:的左、右焦点分别为 , , 且过点 , 则双曲线的渐近线方程为.
-
11、已知直线分别与函数和的图象交于 , , 给出下列三个结论:①;②;③.其中正确结论的个数是( )A、0 B、1 C、2 D、3
-
12、已知抛物线:的焦点为 , 准线为 , 过点的直线与交于不同的两点A,B,为坐标原点,直线与交于点M,若 , 则的面积等于( )A、 B、 C、 D、2
-
13、设为等比数列,则“存在 , 使得”是“为递减数列”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
14、六氟化硫是一种无机化合物,常温常压下为无色无味无毒不燃的稳定气体.化学式为 , 在其分子结构中,硫原子位于中心,六个氟原子均匀分布在其周围,形成一个八面体的结构.如图所示,该分子结构可看作正八面体,记为 , 各棱长均相等,则平面与平面夹角的余弦值是( )
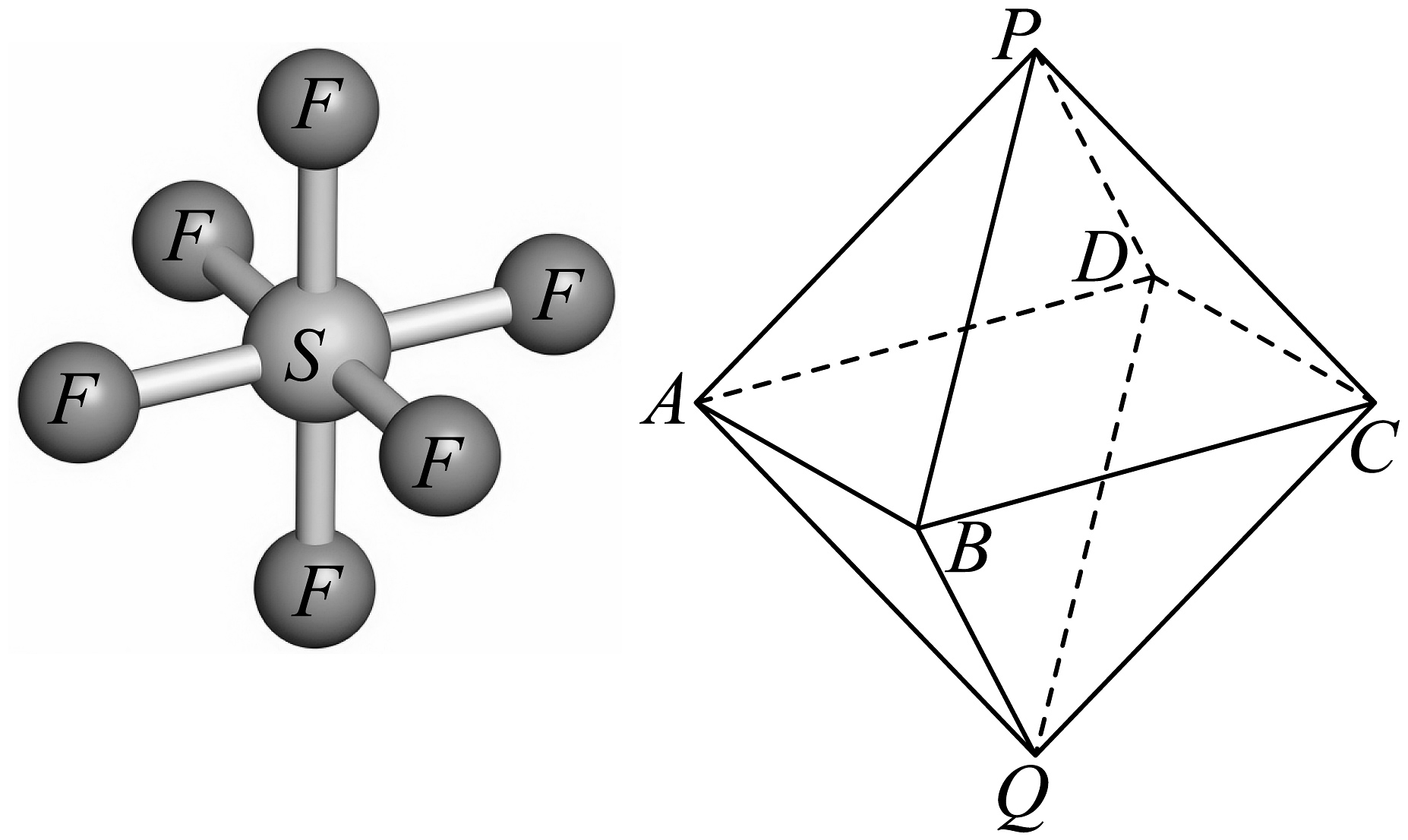 A、 B、 C、 D、
A、 B、 C、 D、 -
15、已知 , 点M满足 , 则的可能取值是( )A、4 B、 C、1 D、
-
16、在天文学中,天体的明暗程度可以用视星等和绝对星等来描述.视星等是在地球上看到的星体亮度等级,视星等受恒星距离影响.绝对星等M是假设把恒星放在距离地球10秒差距(10秒差距≈32.6光年)时的视星等,这样能比较不同恒星本身的亮度.视星等和绝对星等M满足 , 其中是与地球的距离,单位为秒差距.若恒星A距离地球约32.6光年,恒星B距离地球约326光年,恒星A,B的视星等满足 , 则( )A、 B、 C、 D、
-
17、复数的共轭复数为 , 且满足 , 则( )A、2 B、 C、1 D、
-
18、下列函数中,单调递增且值域为的是( )A、 B、 C、 D、
-
19、已知平面向量 , 满足 , , , 则( )A、6 B、3 C、 D、
-
20、已知集合 , 集合 , 则( )A、 B、 C、 D、