相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、在新冠肺炎疫情防控中,核酸检测是新冠肺炎确诊的有效快捷手段.某医院在成为新冠肺炎核酸检测定点医院并开展检测工作的第n天,每个检测对象从接受检测到检测报告生成平均耗时(单位:小时)大致服从的关系为(为常数).已知第9天检测过程平均耗时为16小时,第36天和第40天检测过程平均耗时均为8小时,那么第25天检测过程平均耗时大致为( )A、8小时 B、9.6小时 C、11.5小时 D、12小时
-
2、设函数 , 其中.(1)、若 ,
(i)当时,求的最大值和最小值;
(ii)对任意的 , 都有 , 求实数的取值范围;
(2)、若对任意的 , 都有 , 求实数的取值范围. -
3、已知函数 , 若对于任意的两个不相等实数都有 , 则实数的可能取值是( )A、 B、 C、 D、
-
4、若函数在定义域上的值域为 , 则称为“函数”.已知函数是“函数”,则实数的取值范围是( )A、 B、 C、 D、
-
5、已知是函数的一个零点.则( )A、 B、函数的值域为 C、函数的单调递减区间为 D、不等式的解集为
-
6、若椭圆的长轴长,短轴长分别等于双曲线的实轴长,虚轴长,且椭圆和双曲线的焦点在同一坐标轴上,则称椭圆是双曲线的共轭椭圆,双曲线是椭圆的共轭双曲线.已知椭圆的共轭双曲线为 .(1)、求双曲线的标准方程;(2)、已知点 , 直线(不过点)与相交于、两点,且 , 求点到直线的距离的最大值.
-
7、已知圆:与圆:相交于 , 两点,则直线的方程为( )A、 B、 C、 D、
-
8、已知正四棱柱中, .
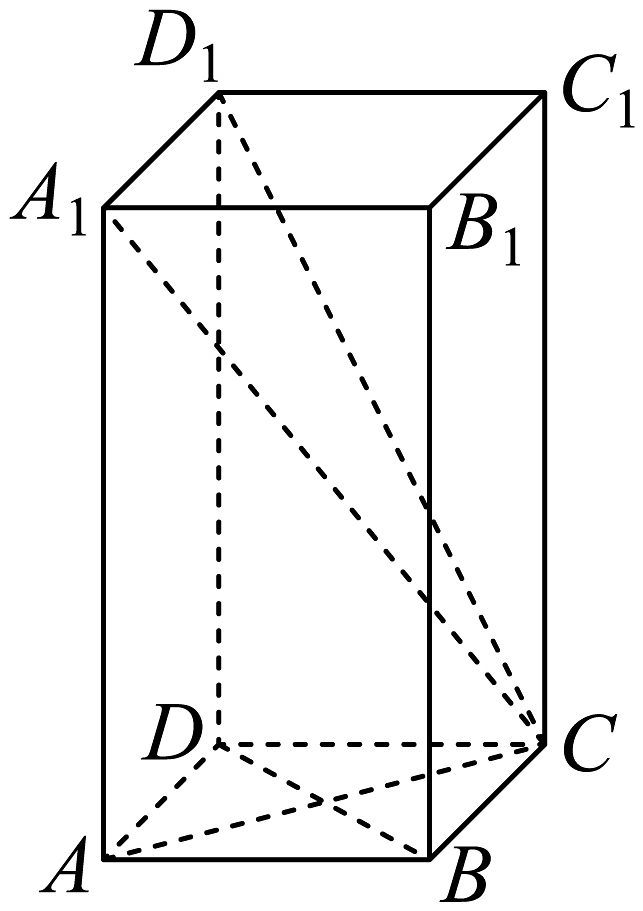 (1)、求证:;(2)、求平面与平面的夹角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由.
(1)、求证:;(2)、求平面与平面的夹角的余弦值;(3)、在线段上是否存在点 , 使得平面平面 , 若存在,求出的值;若不存在,请说明理由. -
9、如图,在棱长为的正方体中,为的中点.
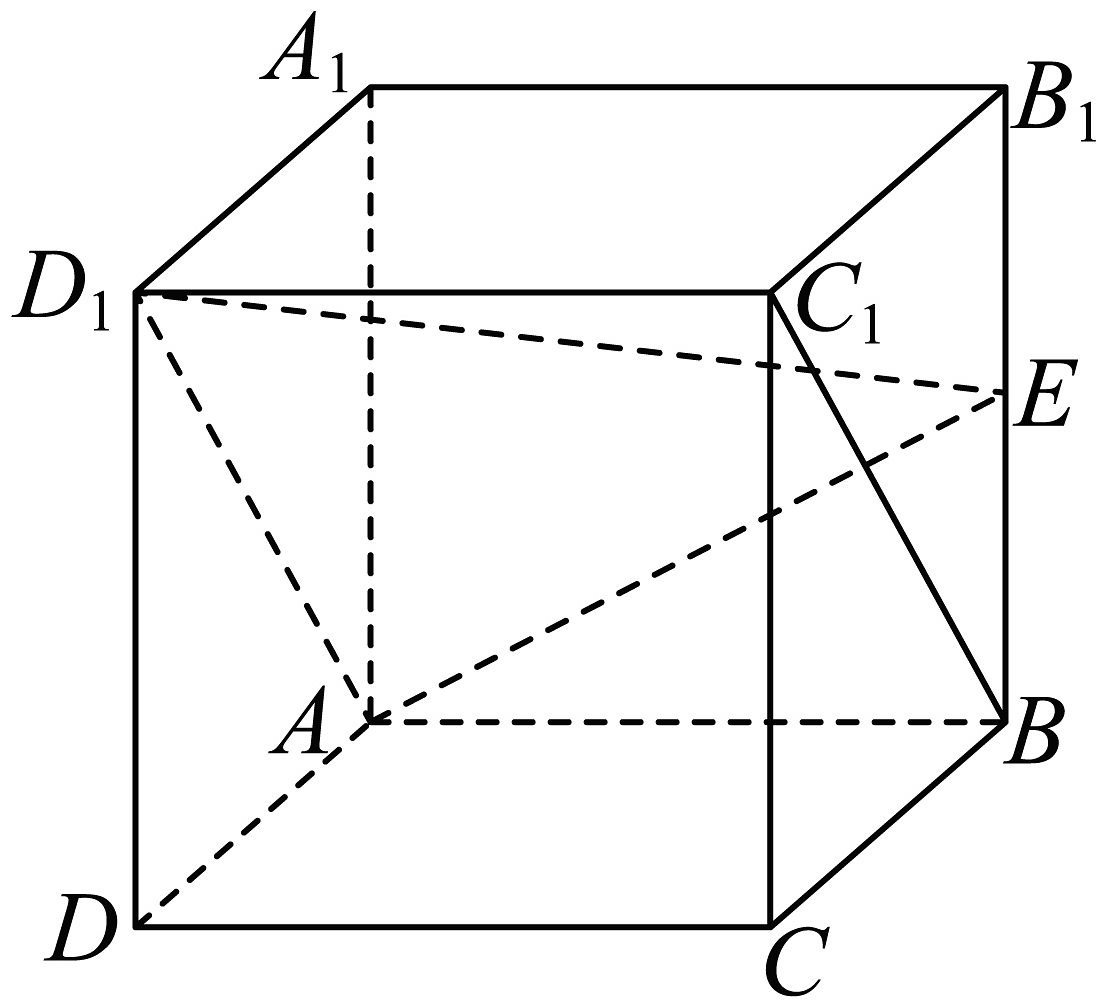 (1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、求点到平面的距离.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、求点到平面的距离. -
10、从4名男生和2名女生中任选3人参加演讲比赛.(1)、将6名学生做适当编号,把选中3人的所有可能情况列举出来;(2)、求所选3人中恰有一名女生的概率;(3)、求所选3人中至少有一名女生的概率
-
11、如图,在四棱锥中,底面是正方形,底面 , E是的中点,已知 , .
 (1)、求证:;(2)、求证:平面平面 .
(1)、求证:;(2)、求证:平面平面 . -
12、一个盒子中装有大小相同的2个红球和个白球,从中任取2个球.
(1)若 , 求取到的2个球恰好是一个红球和一个白球的概率;
(2)若取到的2个球中至少有1个红球的概率为 , 求 .
-
13、一次掷两枚均匀的骰子,得到的点数为m和n,则关于x的方程x2+(m+n)x+4=0无实数根的概率是 .
-
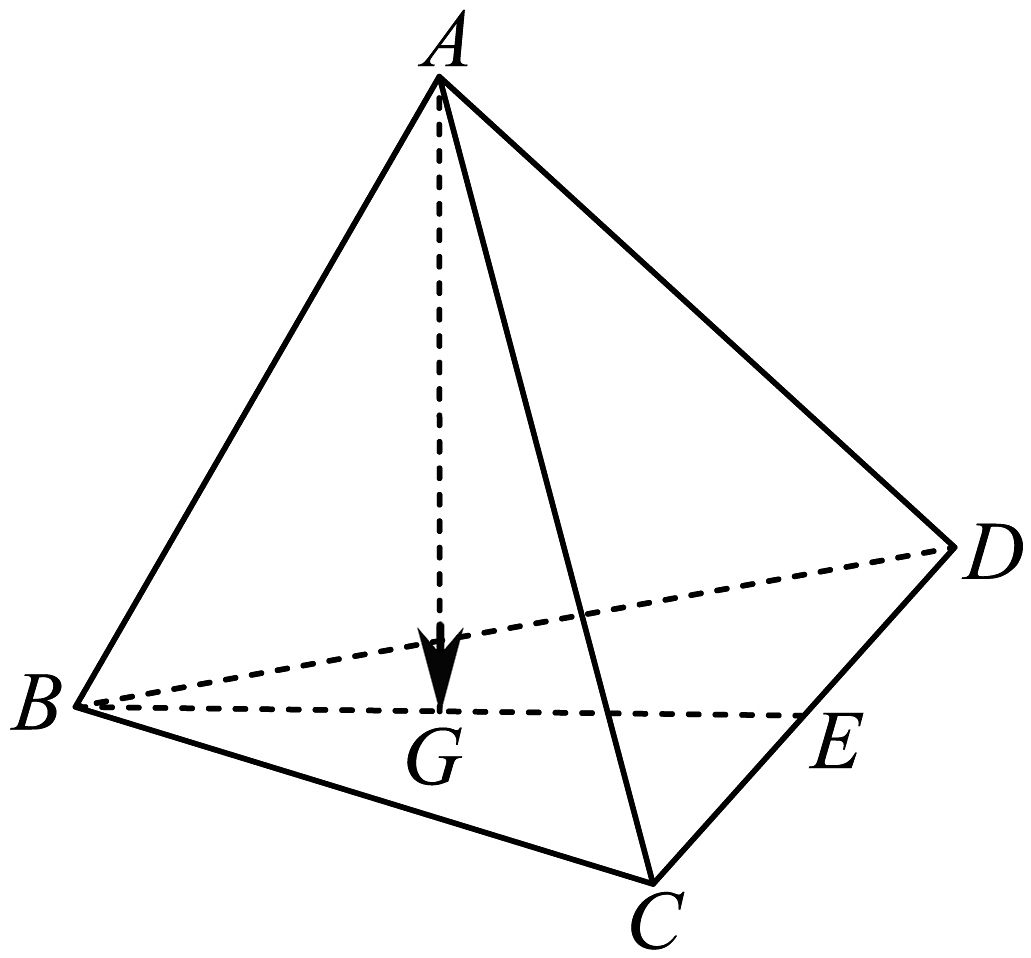
14、在四面体中,、分别是、的中点,若 , 则 .
-
15、已知P(A)=0.4,P(B)=0.2.(1)如果B⊆A,则P(A∪B)= , P(AB)=;(2)如果A,B互斥,则P(A∪B)= , P(AB)=.
-
16、如图,正方体的棱长为1,E,F,G分别为的中点,则下列说法正确的是( )
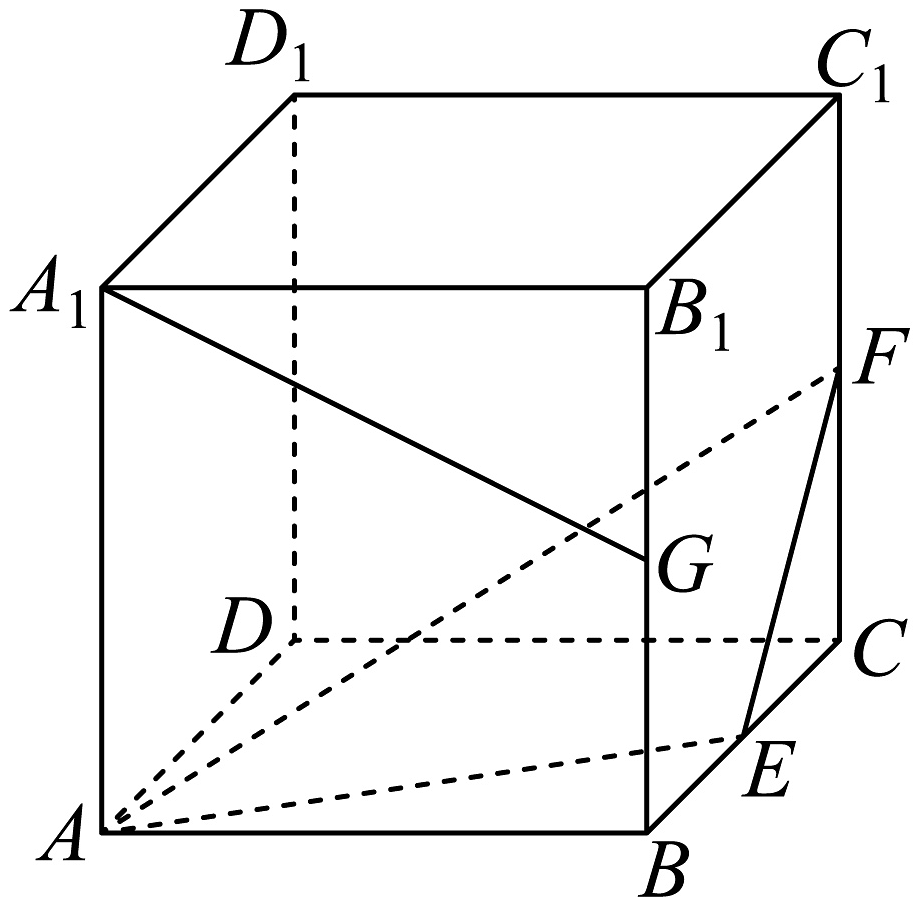 A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、点C与点G到平面的距离相等
A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、点C与点G到平面的距离相等 -
17、下列说法中,正确的是( )A、概率是频率的稳定值,频率是概率的近似值 B、做次随机试验,事件发生次,则事件发生的频率就是事件的概率 C、频率是不能脱离次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值 D、任意事件发生的概率总满足
-
18、如图,在棱长为的正方体中,点是平面内一个动点,且满足 , 则直线与直线所成角的取值范围为( )(参考数据:)
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、中国古代传统文化中,有记录人们出生年份的属相记录法,共有12种属相,分别是鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪,也称子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.现有一个正十二面体,每一个(正五边形)面标有一个属相,如图.现将这个质地均匀的正十二面体先后抛掷两次,则朝上的面两次属相不同的概率是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、若向量与向量互相垂直,则的值为( )A、1 B、2 C、3 D、4