版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知函数 $f (x) = 2 ln x - \frac{1}{2} m x^{2} + 1 (m \in R)$ .

(1)、讨论函数 $f (x)$ 的单调性

(2)、当 $m = 1$ 时，证明： $f (x) < 1$ .

查看解析
2、记 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $3 ({sin}^{2} A + {sin}^{2} C) = 2 sin A sin C + 8 sin A sin C cos B$ ．

(1)、证明： $a + c = 2 b$ ；

(2)、若 $cos B = \frac{11}{14}$ ， $△ A B C$ 的面积为 $\frac{15}{4} \sqrt{3}$ ，求 $△ A B C$ 的周长．

查看解析
3、设函数 $f (x) = \{\begin{array}{l} x - a, x \leq 0 \\ \ln x, x > 0 \end{array}$ ，已知 $x_{1} < x_{2}$ ，且 $f (x_{1}) = f (x_{2})$ ，若 $x_{2} - x_{1}$ 的最小值为 $\frac{1}{e}$ ，则 $a$ 的值为．

查看解析
4、在等比数列 $\{a_{n}\}$ 中， $a_{3} a_{5} = 64, a_{6} = 32$ ，则 $a_{1}$ 的值为.

查看解析
5、已知函数 $f (x) = \{\begin{array}{l} a^{x}, x < 0 \\ a x + a, x \geq 0 \end{array}$ 在 $R$ 上单调递增，则 $a$ 的取值范围是（）

A、 $(0, + \infty)$ B、 $(0, 1)$ C、 $(1, + \infty)$ D、 $[1, + \infty)$

查看解析
6、已知 $2 \sin α - \sin β = \sqrt{3}, 2 \cos α - \cos β = 1$ ，则 $\cos (α - β) =$ （）

A、- $\frac{1}{8}$ B、- $\frac{7}{8}$ C、 $\frac{1}{4}$ D、 $\frac{\sqrt{15}}{4}$

查看解析
7、已知等差数列 $\{a_{n}\}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{2} = 4$ ， $S_{9} = 63$ ，则 $a_{8} =$ （）

A、7 B、8 C、10 D、16

查看解析
8、设复数 $z$ 满足 $(- 1 + i) z = 1 - 3 i$ ，则 $z =$ （）

A、 $- 2 - i$ B、 $- 2 - 2 i$ C、 $1 - 2 i$ D、 $- 2 + i$

查看解析
9、已知集合 $A = \{x |x^{2} < 9\}$ ， $B = \{- 1, 0, 2, 3\}$ ，则 $A \cap B =$ （）

A、 $\{- 1, 0\}$ B、 $\{0, 2\}$ C、 $\{- 1, 0, 2\}$ D、 $\{- 1, 2\}$

查看解析
10、已知函数 $f (x) = \frac{x^{2}}{e^{x}}$ .

(1)、求函数 $f (x)$ 的单调区间；

(2)、求函数 $f (x)$ 的极小值点和极小值；

(3)、若方程 $f (x) = m$ 恰好有2个解，则实数的范围.

查看解析
11、已知 $a, b, c$ 分别为 $△ A B C$ 的内角 $A ､ B ､ C$ 的对边，且 $a sin B = \sqrt{3} b cos A$ .

(1)、求角A；

(2)、若 $a = \sqrt{21}, b = 4$ ，求出 $c$ 边并求出 $△ A B C$ 的面积

查看解析
12、已知函数 $f (x) = \{\begin{cases} x^{2} + 2 x, x \leq 0 \\ \ln x, x > 0 \end{cases}, g (x) = f (x) + x + a$ ．若 $g (x)$ 存在2个零点，则a的取值范围是.

查看解析
13、若角 $α$ 的终边在第四象限，且 $\sin α = - \frac{3}{5}$ ，则 $\tan (\frac{π}{4} + α)$ ＝．

查看解析
14、若 $f (x) = \sin (2 x - \frac{π}{3})$ ，则（）

A、 $f (x)$ 的最小正周期为 $π$ B、 $f (x)$ 关于直线 $x = \frac{π}{2}$ 对称 C、 $f (x)$ 的一个对称点是 $(\frac{π}{6}, 0)$ D、 $f (x)$ 在 $[\frac{π}{6}, \frac{π}{2}]$ 上单调递减

查看解析
15、在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c．若 $a : b : c = 3 : \sqrt{7} : 2$ ，则B等于（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看解析
16、已知向量 $\vec{a} = (x, - 2)$ ， $\vec{b} = (2, 1)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $x =$ （）.

A、 $- 4$ B、4 C、 $- 1$ D、1

查看解析
17、命题“ $\exists x \in (1, + \infty)$ ， $x^{2} + 1 \leq 3 x$ ”的否定是（）

A、 $\forall x \in (- \infty, 1]$ ， $x^{2} + 1 > 3 x$ B、 $\forall x \in (1, + \infty)$ ， $x^{2} + 1 \leq 3 x$ C、 $\exists x \in (- \infty, 1]$ ， $x^{2} + 1 \leq 3 x$ D、 $\forall x \in (1, + \infty)$ ， $x^{2} + 1 > 3 x$

查看解析
18、已知数列 $\{a_{n}\}$ 的首项 $a_{1} = 1$ ，且满足 $a_{n + 1} = \frac{1}{2} a_{n} + \frac{1}{2^{n}}$ ，则此数列的通项公式 $a_{n}$ 等于（）

A、 $2 n$ B、 $n (n + 1)$ C、 $\frac{n}{2^{n - 1}}$ D、 $\frac{n (n + 1)}{2^{n}}$

查看解析
19、如图，在正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A_{1} B_{1} = \sqrt{2}$ ， $A B = 2 \sqrt{2}$ ，该棱台体积 $V = \frac{14 \sqrt{3}}{3}$ ，则该棱台外接球的表面积为．

查看解析
20、已知椭圆 $Γ : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点为 $A (- 2, 0)$ ，下顶点为 $B$ ．且过点 $C (\sqrt{2}, \frac{\sqrt{2}}{2})$ ．

(1)、求点 $B$ 的坐标；

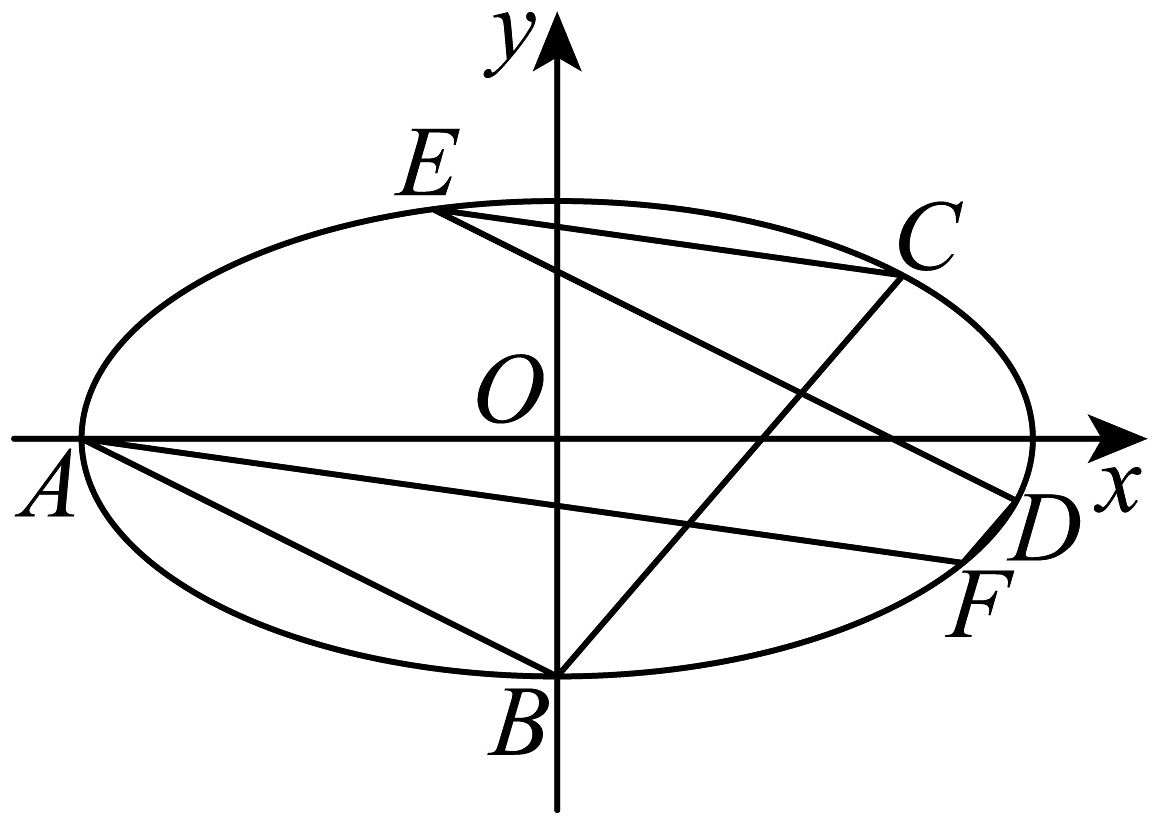(2)、若直线 $l : y = x + m$ 上存在一点P， $Γ$ 上存在一点Q，使 $△ P A Q$ 是以A为直角顶点的等腰直角三角形，求实数m的取值范围；

(3)、若椭圆 $Γ$ 上的三个动点D，E，F满足 $D E / / A B, D F / / B C$ ，证明： $A F / / C E$ ．

查看解析

上一页 792 793 794 795 796 下一页跳转