版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、① $f (x)$ 在 $R$ 上单调递增，② $f (\frac{x_{1} + x_{2}}{2}) = \frac{f (x_{1}) + f (x_{2})}{2}$ ，则满足上述两个条件的函数为（写出一个即可）；

查看解析
2、已知幂函数 $y = f (x)$ 的图像经过点 $(3, \frac{\sqrt{3}}{3})$ ，则这个函数的解析式为 $f (x)$ =

查看解析
3、已知常数 $a > 0$ ， $f (x) = \frac{2^{x}}{2^{x} + a x}$ 的图象经过点 $P (p, \frac{6}{5}), Q (q, - \frac{1}{5})$ ，且 $2^{p + q} = 36 p q$ ，则（）

A、 $a = 6$ B、 $f (x)$ 的图象与 $y = 1$ 无限接近但又不与该直线相交 C、 $\forall x \in (2, + \infty)$ ，不等式 $f (x) > \frac{1}{a - 2}$ 恒成立 D、方程 $f (2 x) = f (x)$ 有且只有一个实数解

查看解析
4、已知函数 $y = f (x)$ 与 $y = g (x)$ 的图象如图所示，则（）

A、 $y = f (x) g (x)$ 为奇函数 B、 $y = f (x) g (x)$ 在 $(0, + \infty)$ 上单调递增 C、 $y = f (g (x))$ 在 $(- \infty, 0)$ 上单调递减 D、 $y = f (x) g (x)$ 的值域为 $R$

查看解析
5、已知 $a$ ， $b$ 为正数，且 $a + b = 1$ ，则（）

A、 $\sqrt{a} + \sqrt{b}$ 的最小值为 $\sqrt{2}$ B、 $a b$ 的最大值为 $\frac{1}{4}$ C、 $a^{2} + b^{2}$ 的最小值为 $\frac{1}{2}$ D、 $\frac{1}{a} + \frac{4}{b}$ 的最小值为3

查看解析
6、设a，b∈R，定义运算“∧”和“∨”如下：a∧b＝ $\{\begin{matrix} a, a \leq b \\ b, a > b \end{matrix}$
a∨b＝ $\{\begin{matrix} b, a \leq b \\ a, a > b \end{matrix}$ 若正数a，b，c，d满足ab≥4，c＋d≤4，则(　　)

A、a∧b≥2，c∧d≤2 B、a∧b≥2，c∨d≥2 C、a∨b≥2，c∧d≤2 D、a∨b≥2，c∨d≥2

查看解析
7、已知函数 $f (x) = \frac{1 + x}{1 - x}$ ，若 $y = f (x + a) - b$ 为奇函数，则（）

A、 $a = 1, b = - 1$ B、 $a = 1, b = 1$ C、 $a = - 1, b = - 1$ D、 $a = - 1, b = 1$

查看解析
8、已知函数 $f (x) = \sqrt[n]{x^{n}}$ ， $g (x) = x, n > 1$ ， $n \in N^{*}$ ，则“ $n$ 为奇数”是“ $f (x), g (x)$ 是同一个函数”的（）

A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件

查看解析
9、已知函数 $f (x) = x^{2} - k x - 8$ 在 $[3, 4]$ 上具有单调性，则实数 $k$ 的取值范围是（）

A、 $[6, 8]$ B、 $(- \infty, 6] \cup [8, + \infty)$ C、 $[8, + \infty)$ D、 $(- \infty, 6]$

查看解析
10、函数 $f (x) = \frac{\sqrt{4 - x}}{x - 1}$ 的定义域为（）

A、 $(- \infty, 4]$ B、 $(1, 4]$ C、 $(- \infty, 1) \cup (1, + \infty)$ D、 $(- \infty, 1) \cup (1, 4]$

查看解析
11、函数 $f (x) = 3^{x} + 1$ ，则 $f (x)$ 的值域为（）

A、 $(1, + \infty)$ B、 $[1, + \infty)$ C、 $(0, + \infty)$ D、 $[0, + \infty)$

查看解析
12、已知函数 $f (x) = \{\begin{array}{l} x (x + 4), x \geq 0 \\ x (x - 4), x < 0 \end{array}$ ，则 $f (- 3) =$ （）

A、21 B、 $- 3$ C、 $- 21$ D、3

查看解析
13、直线 $l_{1}$ 经过点 $A (- 2, 0)$ ，倾斜角为 $α, 0 < α < \frac{π}{2}$ ，直线 $l_{2}$ 经过点 $B (2, 0)$ ，倾斜角为 $α + θ$ .两直线相交于点P.

(1)、若 $θ = \frac{π}{4}$ ；
（i）请用 $\tan α$ 表示线段PB中点Q的坐标；
（ⅱ）求证：线段PB中垂线过定点.

(2)、当 $α = \frac{π}{6}, θ = \frac{π}{3}$ 时，椭圆 $τ$ 以A、B为焦点，且经过点P，H为椭圆 $τ$ 的上顶点.
（i）求椭圆 $τ$ 的标准方程；
（ⅱ）若直线 $y = k x + m$ 与椭圆 $τ$ 交于M、N，若 $H M = H N$ .求k的取值范围.

查看解析
14、已知直线 $x - y + 2 = 0$ 和圆 $C : x^{2} + y^{2} - 8 x + 12 = 0$ ，过直线上的一点 $P (x_{0}, y_{0})$ 作两条直线PA，PB与圆C相切于A，B两点，如下图所示.

(1)、当P点坐标为 $(2, 4)$ 时，求以PC为直径的圆的方程，并求直线AB的方程；

(2)、直线l经过点P，与圆C交于M，N两点求 $P M \cdot (P M + P N)$ 的最小值.

查看解析
15、在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $2 B C = 2 B B_{1} = B A = 2$ ，点M为棱 $A A_{1}$ 上的动点（含端点）.

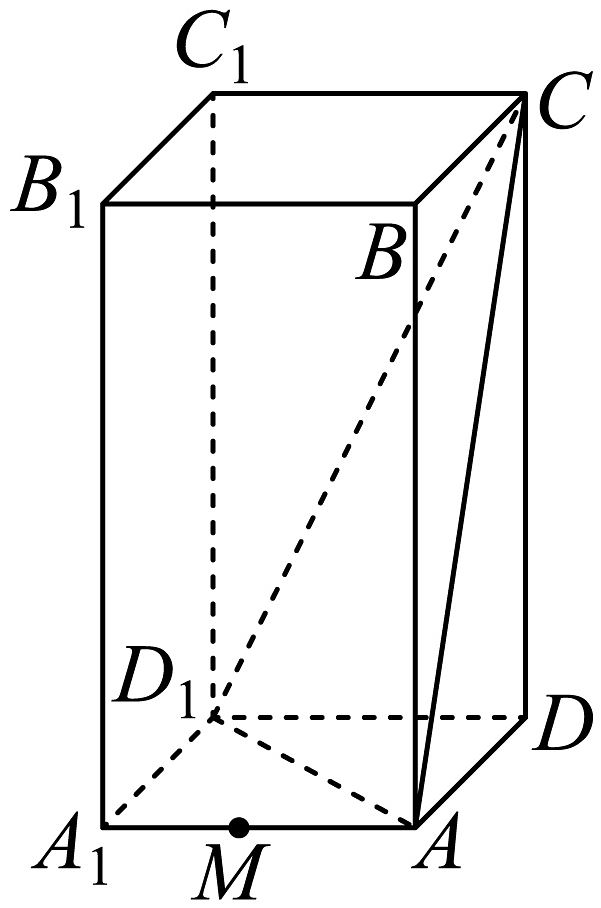(1)、求二面角 $A - D_{1} C - D$ 的余弦值；

(2)、当 $A M$ 的长度为何值时，直线 $B_{1} M$ 与平面 $A C D_{1}$ 所成角的正弦值最小，并求出最小值.

查看解析
16、在正四面体 $O - A B C$ 中，E，F，G，H分别是OA，AB，BC，OC的中点.设 $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}, \vec{O C} = \vec{c}$ .

(1)、用 $\vec{a}, \vec{b}, \vec{c}$ 表示 $\vec{E F}, \vec{F G}$ ；

(2)、求证：FH与GE相交；

(3)、求证：四边形EFGH为矩形.

查看解析
17、已知 $A (1, 3), B (2, - 1)$ .

(1)、求AB的中垂线方程；

(2)、求经过A、B两点的椭圆的标准方程.

查看解析
18、正四面体 $A - B C D$ 的边长为6，其外接球球心为点O，P为CD边的中点，点Q在 $△ A B C$ 内部及边上运动，则 $\vec{P O} \cdot \vec{P Q}$ 取值范围为.

查看解析
19、一个圆经过椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{3} = 1$ 的三个顶点，且圆心在y的正半轴上，则该圆的标准方程为.

查看解析
20、两条平行直线 $3 x + 4 y - 5 = 0$ 与 $6 x + b y + 10 = 0$ 间的距离是.

查看解析

上一页 790 791 792 793 794 下一页跳转