相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、环境污染已经触目惊心,环境质量已经成为“十三五”实现全面建成小康社会奋斗目标的短板和瓶颈.绵阳某化工厂每一天中污水污染指数与时刻(时)的函数关系为其中为污水治理调节参数,且。(1)、若 , 求一天中哪个时刻污水污染指数最低;(2)、规定每天中的最大值作为当天的污水污染指数,要使该厂每天的污水污染指数不超过 , 则调节参数a应控制在什么范围内?
-
2、设 . 注:(1)、证明:;(2)、若 , 求的最小值.
-
3、已知集合 .(1)、若 , 求;(2)、从①;②;③这三个条件中任选一个,补充在下面的横线上,并进行解答.
问题:若_________,求实数的取值范围.
-
4、已知函数 , 若的图象上存在不同的两个点关于原点对称,则实数的取值范围为 .
-
5、已知 , 且 , 则的取值范围为.
-
6、集合 , 则符合条件的集合的个数为 .
-
7、已知函数是定义在R上的函数.对任意 , 总有 , , 且时,恒成立.则( )A、 B、是偶函数 C、在上单调递减 D、(注:)
-
8、已知是奇函数,则( )A、 B、在上单调递增 C、的值域为 D、的解集为
-
9、下列说法正确的有( )A、 B、“”是“”的充分不必要条件 C、“”是“”的充要条件 D、“”是“”的必要不充分条件
-
10、已知函数在定义域上单调,若对任意的 , 都有 , 则方程的解的个数为( )A、0 B、1 C、2 D、3
-
11、函数的值域为( )A、 B、 C、 D、
-
12、镜片的厚度是由镜片的折射率决定,镜片的折射率越高,镜片越薄,同时镜片越轻,也就会带来更为舒适的佩戴体验.某次社会实践活动中,甲、乙、丙三位同学分别制作了三种不同的树脂镜片,折射率分别为 , 则这三种镜片中,制作出最薄镜片和最厚镜片的同学分别为( )A、丙同学和甲同学 B、乙同学和甲同学 C、甲同学和丙同学 D、乙同学和丙同学
-
13、函数的图象如图所示,则该函数的定义域和单调区间分别是
 A、和 B、和 C、和 D、和
A、和 B、和 C、和 D、和 -
14、如图,把直截面半径为的圆柱形木头锯成直截面为矩形的木料,如果矩形的一边长为(单位:),面积为(单位:),则把表示为的函数的解析式为( )
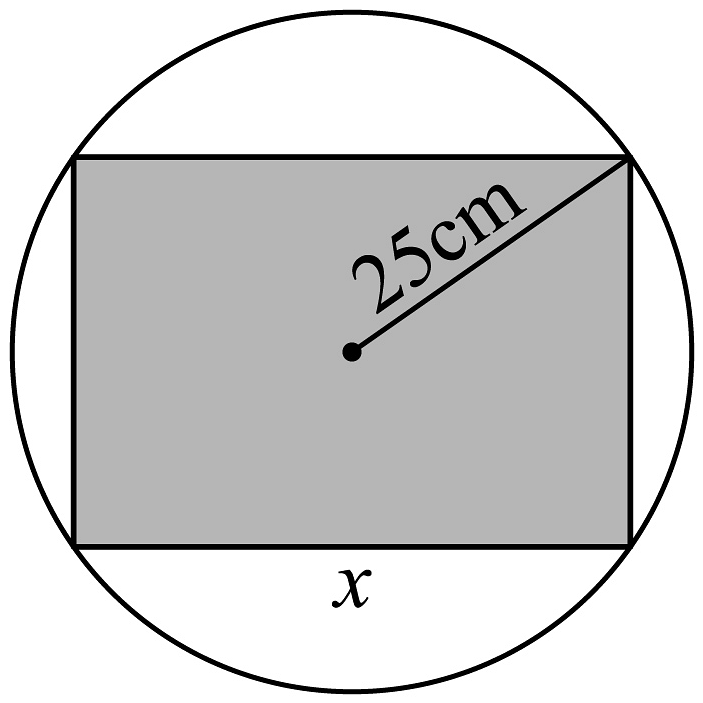 A、 B、 , C、 D、 ,
A、 B、 , C、 D、 , -
15、命题“ , 使得”的否定为( )A、 , B、 , 使得 C、 , D、 , 使得
-
16、已知集合 , 集合 , , 则图中阴影部分表示的集合为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、某服装厂拟在2021年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m万件与年促销费用万元满足 . 已知2021年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(此处计算每件产品年平均成本时,产品成本仅包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2021年该产品的利润y万元表示为年促销费用x万元的函数;(利润=收入-成本);
(2)该服装厂2021年的促销费用投入多少万元时,利润最大.
-
18、已知函数.(1)、求的值;(2)、探索;(3)、利用(2)中结论,求的值.
-
19、已知函数是一次函数,且满足.(1)、求的解析式;(2)、若 , 求的最小值.
-
20、解关于的不等式.(1)、;(2)、;(3)、.