相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、已知全集 .
(1)求;
(2)求 .
-
2、已知定义在上的运算“”: , 若 , 则关于的不等式的解集为.
-
3、已知函数 , 当时,则函数的值域为 , 的最小值是.
-
4、已知集合 , 若 , 则实数a的值可以是( ).A、 B、 C、0 D、
-
5、已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、
-
6、某中学高中学生运动会,一班46名学生中有15名学生没有参加比赛,参加比赛的学生中,参加田赛的有16人,参加径赛的有23人,则田赛和径赛都参加的学生人数为( ).A、7 B、8 C、10 D、12
-
7、下列四组函数,表示同一函数的是( )A、 B、 C、 D、
-
8、不等式的解集为 .
-
9、已知函数则( )A、 B、1 C、2 D、5
-
10、在数列中, , , 对满足的任意正整数m,n,p,q,都有成立.(1)、若数列是等比数列,求a,b满足的条件;(2)、若 , , 设.
①求数列的通项公式;
②求证:.
-
11、在四棱锥中, , , 底面 , 点O在上,且.
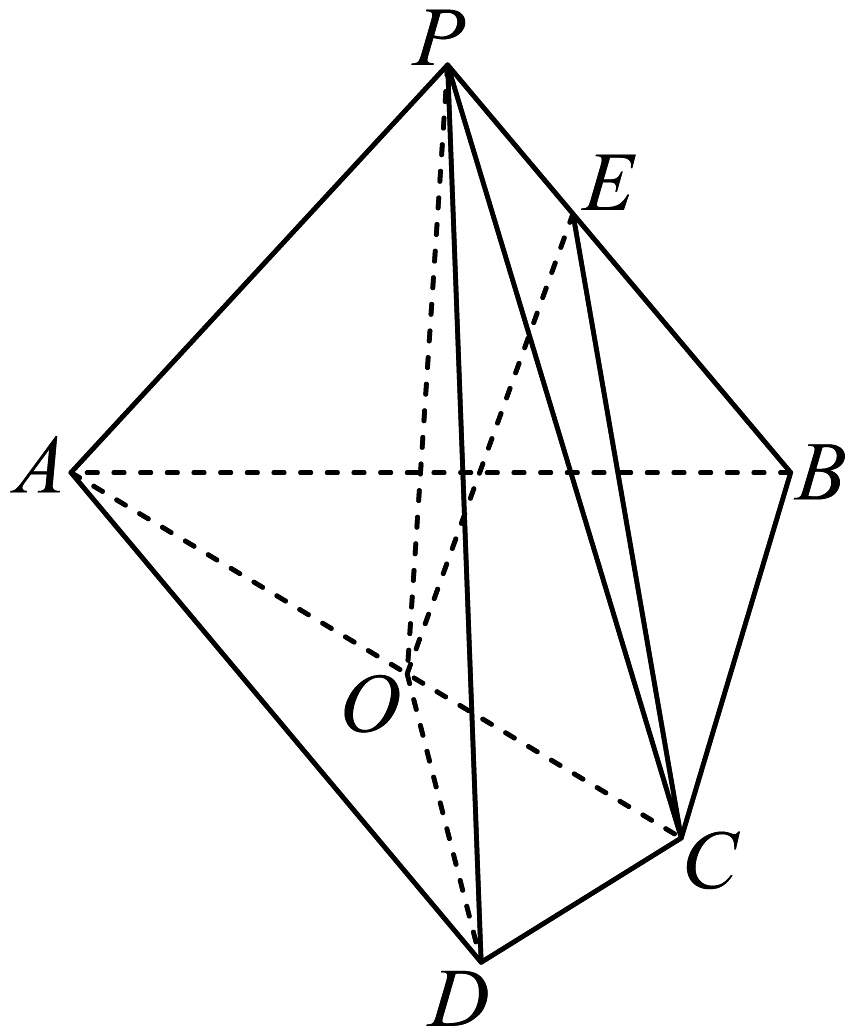 (1)、求证:;(2)、若 , , 点在上,平面 , 求的值;(3)、若 , 二面角的正切值为 , 求二面角的余弦值.
(1)、求证:;(2)、若 , , 点在上,平面 , 求的值;(3)、若 , 二面角的正切值为 , 求二面角的余弦值. -
12、设函数.(1)、求函数在处的切线方程;(2)、若恒成立,求证:m的最大值与最小值之差大于.
-
13、设 , 分别为双曲线的左、右焦点,过的直线交双曲线于A,B两点,且.(1)、求的长(用a,b表示);(2)、若双曲线的离心率 , 求证:.
-
14、在一次联考中,经统计发现,甲乙两个学校的考生人数都为1000人,数学均分都为94,标准差都为12,并且根据统计密度曲线发现,甲学校的数学分数服从正态分布,乙学校的数学分数不服从正态分布.(1)、甲学校为关注基础薄弱学生的教学,准备从70分及以下的学生中抽取10人进行访问,学生小A考分为68分,求他被抽到的概率大约为多少;(2)、根据统计发现学校乙得分不低于130分的学生有25人,得分不高于58分的有1人,试说明乙学校教学的特点;
参考数据:若 , 则 , , .
-
15、表示不超过x的最大整数,设 , , 则;(用M,N表示).
-
16、已知:当无穷大时,的值为 , 记为.运用上述结论,可得.
-
17、若函数在处取得最大值,则.
-
18、设点P为正方体的上底面上一点,下列说法正确的有( )A、存在点P,使得与平面所成角为 B、存在点P,使得点A,分别到平面的距离之和等于 C、存在点P,使得点A,分别到平面的距离之和等于 D、存在点P,使得与平面所成角为
-
19、已知点M是抛物线与圆的交点,点F为抛物线C的焦点,则下列结论正确的有( )A、的最小值为2 B、圆E与抛物线C至少有两条公切线 C、若圆E与抛物线C的准线相切,则轴 D、若圆E与抛物线C的准线交于P,Q两点,且 , 则
-
20、关于函数 , 下列说法正确的有( )A、函数可能没有零点 B、函数可能有一个零点 C、函数一定是中心对称图形 D、函数可能是轴对称图形