-
1、有一个等腰三角形纸片，若能从一个底角的顶点出发，将其剪成两个等腰三角形纸片，则原等腰三角形纸片的顶角为度.
-
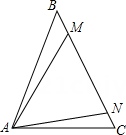
2、如图，在△ABC中，AB=BC，在BC上取点M，在MC上取点N，使MN=NA，若∠BAM=∠NAC，则∠MAC=.
-
3、已知△ABC中，AB=AC，∠BAC=120°.
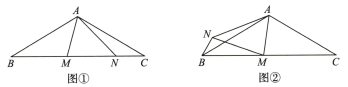(1)、如图①，点 M，N 在底边 BC上，且∠ANB=45°，∠MAN=60°.请在图①中AN 上方作出∠NAD=60°，且AD=AM，连接ND，CD，并直接写出 BM与CN的数量关系.(2)、如图②，点M在BC上，点 N在BC的上方，且∠MBN=∠MAN=60°，求证：MC=BN+MN. -
4、已知△ABC，AB=AC，D 为直线BC 上一点，E 为直线AC 上一点，AD=AE，设∠BAD=α，∠CDE=β.
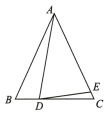(1)、如图，若点 D 在线段BC 上，点 E 在线段AC 上.①如果∠ABC=60°，∠ADE=70°，那么α= ▲ °，β= ▲ °.
②求α，β之间的关系式.
(2)、是否存在不同于以上②中的α，β之间的关系式?若存在，求出这个关系式(求出一个即可)；若不存在，说明理由. -
5、如图，在△ABC 中，∠ACB=90°，AC=AE，BC=BF，则∠ECF=( ).
A、60° B、45° C、30° D、不确定 -
6、在等腰△ABC中，AB=AC，一边上的中线 BD 将这个三角形的周长分成15 和12 两个部分，则这个等腰三角形的底边长为( ).A、7 B、11 C、7 或11 D、7 或10
-
7、如图，已知BD 为△ABC的角平分线，且BD=BC，E 为BD 延长线上一点，BE=BA，过点E作EF⊥AB 于F，下列结论：
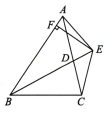
①∠BCE+∠BDC=180°；②AD=AE=EC；③AB∥CE；④BA+BC=2BF.其中正确结论的序号是.
-
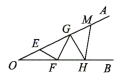
8、如图，AOB 是一钢架，且∠AOB=10°，为使钢架更加坚固，需在其内部添加一些钢管EF，FG，GH……添加的钢管长度都与OE 相等，则最多能添加这样的钢管根.
-
9、如图，在△ABC中，点 D 是BC上一点， 则 .
-
10、等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数为.
-
11、操作：如图，△ABC 是正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以 D 为顶点作一个60°角，角的两边分别交 AB，AC 边于M，N 两点，连接MN.
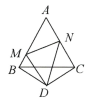(1)、探究：线段 BM，MN，CN 之间的关系，并加以证明.(2)、若点 M，N分别是射线AB，CA 上的点，其他条件不变，再探索线段 BM，MN，NC 之间的关系. -
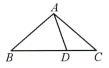
12、如图，已知△ABC 中，点 D 在边BC上，AC=BD，∠CAD=30°，∠ACB=40°，求∠ABC的度数.
-
13、如图，在△ABC中，∠ABC=45°，AM⊥BC于M，D为AM上一点，MD=MC，点E是△ABC 外一点，EC=AC，连接ED 并延长交BC 于点F，且 F 是线段BC 的中点，求证：∠BDF=∠CEF.
-
14、 如图，在△ABC 中，D 在AC 上，E 在AB上，且AB=AC，BC=BD，AD=DE=BE，则∠A的度数为( ).
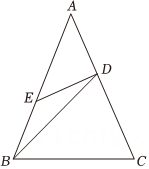A、30° B、45° C、60° D、75° -
15、 已知等腰三角形ABC 中，AB=AC，D 为BC 边上一点，连接 AD，若△ACD 和△ABD 都是等腰三角形，则∠C 的度数是.
-
16、在平面直角坐标系中，已知A(0，4)，B(-4，0)，点C 为x轴上的点，△ABC的面积为2.
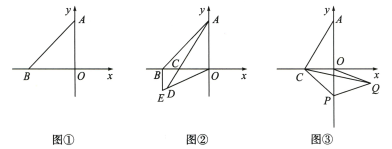(1)、如图①，求点C 的坐标.(2)、如图②，若点C在点B 的右侧，连接AC并延长至点D，使得DO=AO，过点B 作BE∥y 轴交OD 的延长线于点E，求OE—BE 的值.(3)、如图③，若点C 在点B 的右侧，点 P 为y 轴上一动点，以CP 为腰作等腰△CPQ，使PC=PQ，∠CPQ=2∠ACO=2α(α为定值)，AC=5，连接OQ，求线段OQ的最小值. -
17、如图，△ABC中，AB=AC，∠BAC=α，M 为BC 的中点，点 D 在MC 上，以点A 为中心，将线段AD 顺时针旋转α得到线段AE，连接BE，DE.
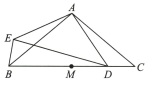(1)、比较∠BAE 与∠CAD 的大小；用等式表示线段 BE，BM，MD之间的数量关系，并证明.(2)、过点 M 作AB 的垂线，交 DE 于点N，用等式表示线段 NE 与ND 的数量关系，并证明. -
18、在等腰Rt△ABC中，∠BAC=90°，AB=AC，直线MN 过点A 且MN∥BC.以点B 为一锐角顶点作 Rt△BDE，∠BDE=90°，且点 D 在直线MN 上(不与点 A 重合).
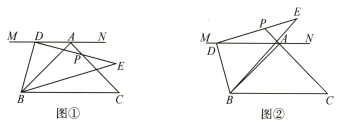(1)、如图①，当DE与AC 交于点P 时，求证：BD=DP.(2)、如图②，当DE 与CA 延长线交于点P 时，BD=DP 是否成立?如果成立，请给予证明；如果不成立，请说明理由. -
19、如图，△ABC 和△CDE 均为等腰直角三角形，点 B，C，D 在一条直线上.点 M是AE的中点，下列结论：①S△ABC+S△CDE≥S△ACE；②BM⊥DM；③BM=DM.正确结论的个数是( ).
A、1 B、2 C、3 D、无法确定 -
20、在平面直角坐标系中，已知点A(1，1)，B(3，2)，点C 在坐标轴上，若△ABC 是等腰三角形，则点C 的个数是( ).A、3 B、4 C、7 D、8