-
1、如图,点E 在△DBC 的边DB 上,点A 在△DBC 的内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:

①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④.
其中正确的是( ).
A、①②③④ B、②④ C、①②③ D、①③④ -
2、如图,若Rt△ABC 两直角边上的中线分别为AE 和BD,则. 与AB2 的比值为( ).
 A、 B、1 C、 D、
A、 B、1 C、 D、 -
3、如图,在△ABC 中, , 点 D,E 都在边 BC 上,∠DAE=60°,若BD=2CE,则DE 的长为.
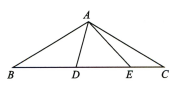
-
4、我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助用这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为.

-
5、如图,在△ABC中,∠ABC=45°,CD⊥AB 于D点,BE⊥AC 于E 点,F 为BC 中点,BE 与DF,DC分别交于点G,H,∠ABE=∠CBE.
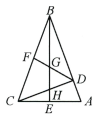 (1)、求证:BH=AC.(2)、求证: .
(1)、求证:BH=AC.(2)、求证: . -
6、如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高为( ).
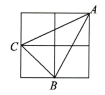 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图,在四边形ABCD中,AC=BC,∠ACB=90°,AD⊥BD.若 , 则线段AB 的长为.

-
8、如图,在Rt△ABC中,∠ABC=90°,AB=BC= , 将△ABC 绕点C 逆时针旋转60°,得到△MNC,连接 BM,则 BM 的长为.
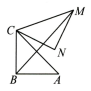
-
9、
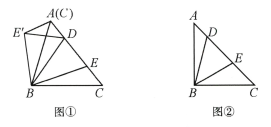 (1)、如图①,在△ABC 中,BA=BC,D,E 是AC 边上的两点,且满足 , 以点 B 为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE'A,连接DE',求证: ;(2)、如图②,在△ABC中,BA=BC,∠ABC=90°,D,E是AC 边上的两点,且满足 求证: .
(1)、如图①,在△ABC 中,BA=BC,D,E 是AC 边上的两点,且满足 , 以点 B 为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE'A,连接DE',求证: ;(2)、如图②,在△ABC中,BA=BC,∠ABC=90°,D,E是AC 边上的两点,且满足 求证: . -
10、如图,在等腰直角△ABC 中,∠ACB=90°,P 是线段BC上一动点(与点B,C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点 Q作QH⊥AP 于点H,交 AB 于点M.
 (1)、若∠PAC=α,求∠AMQ 的大小(用含α的式子表示).(2)、用等式表示线段 MB 与PQ 之间的数量关系,并证明.
(1)、若∠PAC=α,求∠AMQ 的大小(用含α的式子表示).(2)、用等式表示线段 MB 与PQ 之间的数量关系,并证明. -
11、如图,梯子 AB 斜靠在墙面上,AC⊥BC,AC=BC,当梯子的顶端 A 沿AC 方向下滑 xm时,梯足 B 沿CB 方向滑动ym,则x 与y的大小关系是( ).
 A、x=y B、x>y C、x<y D、不确定
A、x=y B、x>y C、x<y D、不确定 -
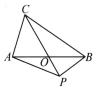
12、如图,在△ABC 中,AB =BC=4,AO=BO,P 是射线CO上的一个动点, , 则当△PAB 为直角三角形时,AP 的长为.
-
13、如图,在等腰直角中,为斜边上的中线.
 (1)、如图1,平分交于E,交于F,若 , 求的长;(2)、将图1中的绕点D顺时针旋转一定角度得到 , 如图2,P,Q分别为线段的中点,连接 , 求证:;(3)、如图3,将绕点A顺时针旋转一定角度到 , 其中D的对应点是M,C的对应点是N,若B,M,N三点在同一直线上,H为中点,连接 , 猜想之间的数量关系,请直接写出结果.
(1)、如图1,平分交于E,交于F,若 , 求的长;(2)、将图1中的绕点D顺时针旋转一定角度得到 , 如图2,P,Q分别为线段的中点,连接 , 求证:;(3)、如图3,将绕点A顺时针旋转一定角度到 , 其中D的对应点是M,C的对应点是N,若B,M,N三点在同一直线上,H为中点,连接 , 猜想之间的数量关系,请直接写出结果. -
14、如图,内接于 , , 为的直径,过点作直线的垂线,垂足为 .
 (1)、求证:是的切线;(2)、若的半径 , , 求的长.
(1)、求证:是的切线;(2)、若的半径 , , 求的长. -
15、解分式方程:
-
16、如图,已知点为⊙O外一点.尺规作图:
(1)连接 , 作线段的中点;
(2)以点为圆心,以线段的长为半径作⊙C,与⊙O交于 , 两点;
(3)作射线 , .
不再另外添加辅助线和字母,请根据以上信息写出一个正确结论: .

-
17、如图,在中,垂直平分 , 延长至点E, , 则 .

-
18、【实际情境】
手工课堂上,老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.

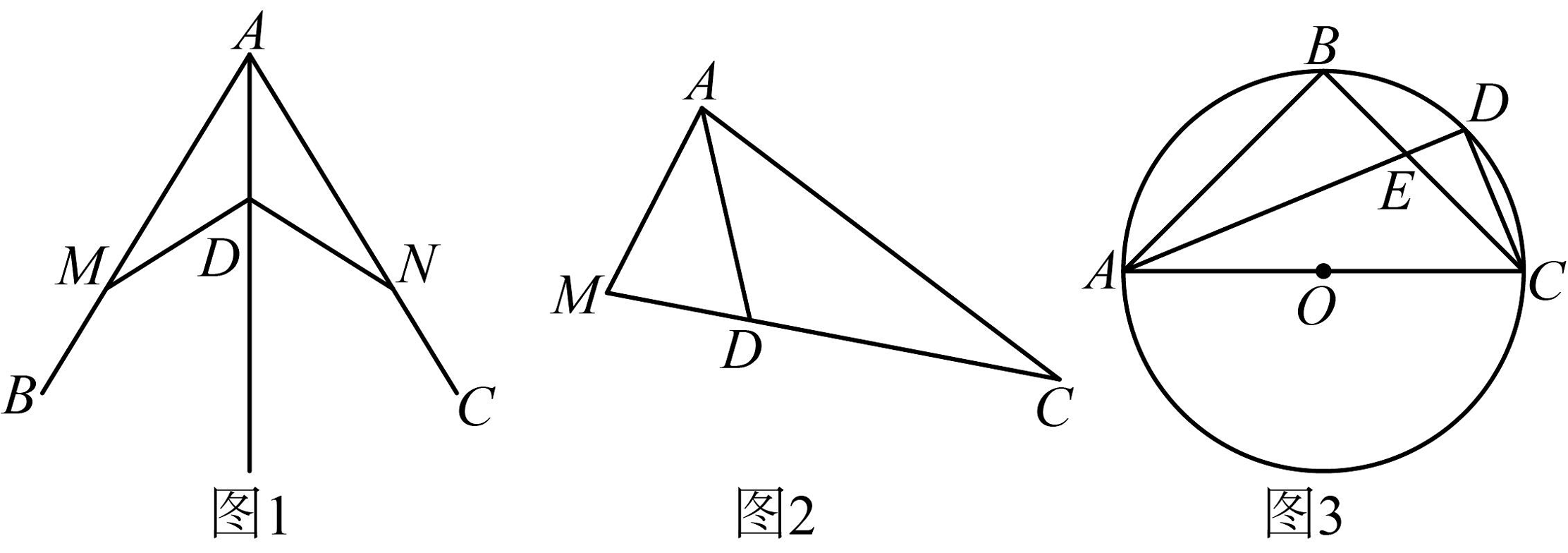
【模型建立】
(1)如图1,从花折伞中抽象出“伞形图”. , . 求证: .
【模型应用】
(2)如图2,中,的平分线交于点 . 请你从以下两个条件:
①;②中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注:只需选择一种情况作答)
【拓展提升】
(3)如图3,为的直径, , 的平分线交于点 , 交于点 , 连接 . 求证: .
-
19、如图,一次函数的图像与反比例函数的图像交于 , 两点,与坐标轴交于、两点,连接 , .
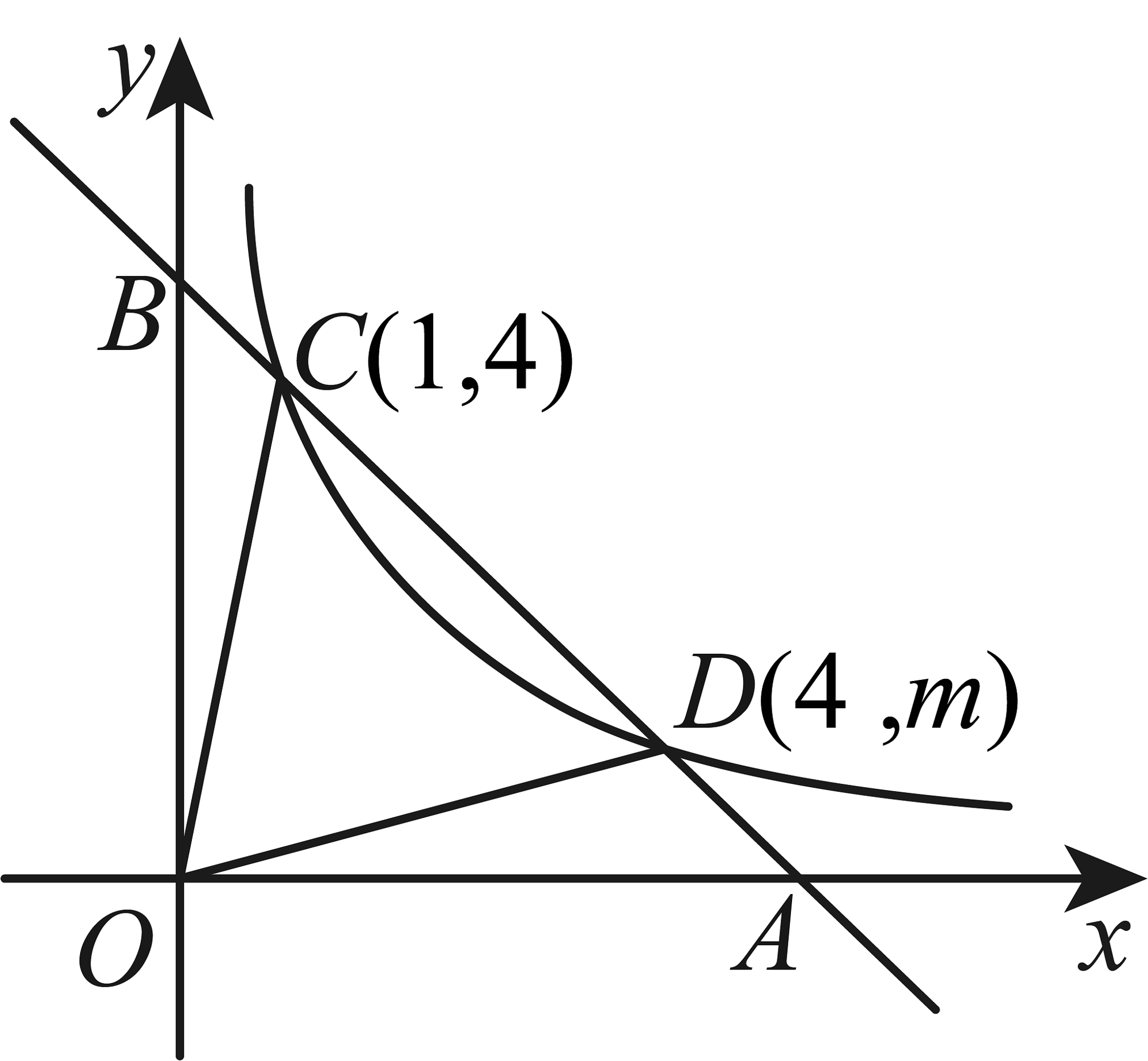 (1)、求一次函数与反比例函数的表达式;(2)、将直线向下平移多少个单位长度,直线与反比例函数图象只有一个交点?
(1)、求一次函数与反比例函数的表达式;(2)、将直线向下平移多少个单位长度,直线与反比例函数图象只有一个交点? -
20、黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的处,测得黄鹤楼顶端的俯角为 , 底端的俯角为 , 求黄鹤楼的高度(参考数据:).
