-
1、若方程的两根分别为 , , 且 , 则m的取值范围为( )A、 B、或 C、 D、
-
2、如图,与在一条直线上, , 将图(2)的三角形截去一块,使他变为与图(1)相似的图形,下列做法不正确的是( )
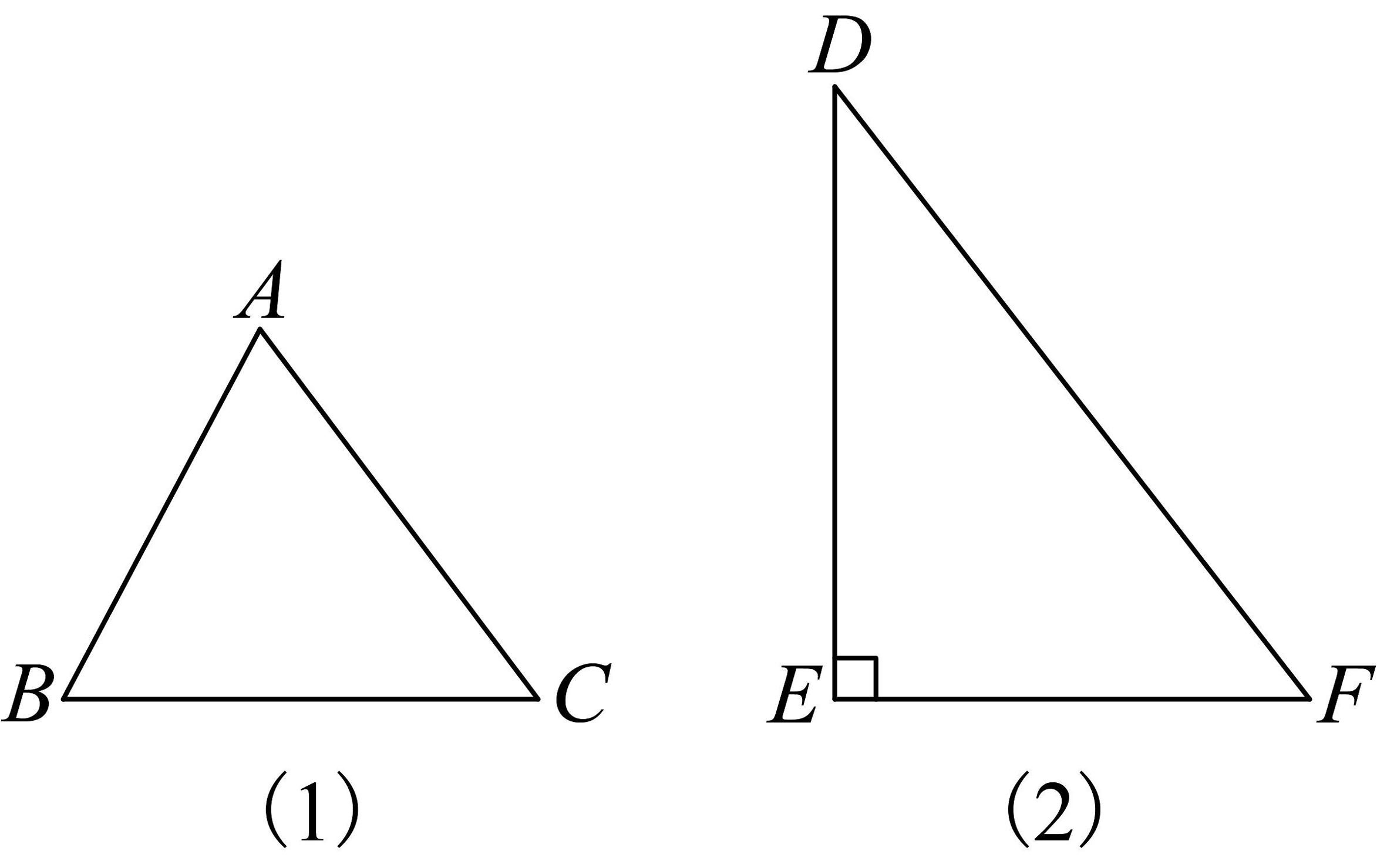 A、过点E作 , 交于点G,则 B、取的中点M,连接 , 则 C、在线段和上分别取点M、N,使得 , 则 D、在上取一点G,使得 , 则
A、过点E作 , 交于点G,则 B、取的中点M,连接 , 则 C、在线段和上分别取点M、N,使得 , 则 D、在上取一点G,使得 , 则 -
3、一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为 , 每挂重物体,弹簧伸长 . 在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )A、 B、 C、 D、
-
4、在平行四边形中,对角线、相交于点 , 添加一个条件,可以得到平行四边形是矩形的是( )A、 B、 C、 D、
-
5、一个多项式因式分解后的一个因式为 , 这个多项式可能是( )A、 B、 C、 D、
-
6、如图所示,小华测得一个圆规的一条支脚长为 , 另一只脚长为 , 则该圆规不可能画出圆的半径为( )
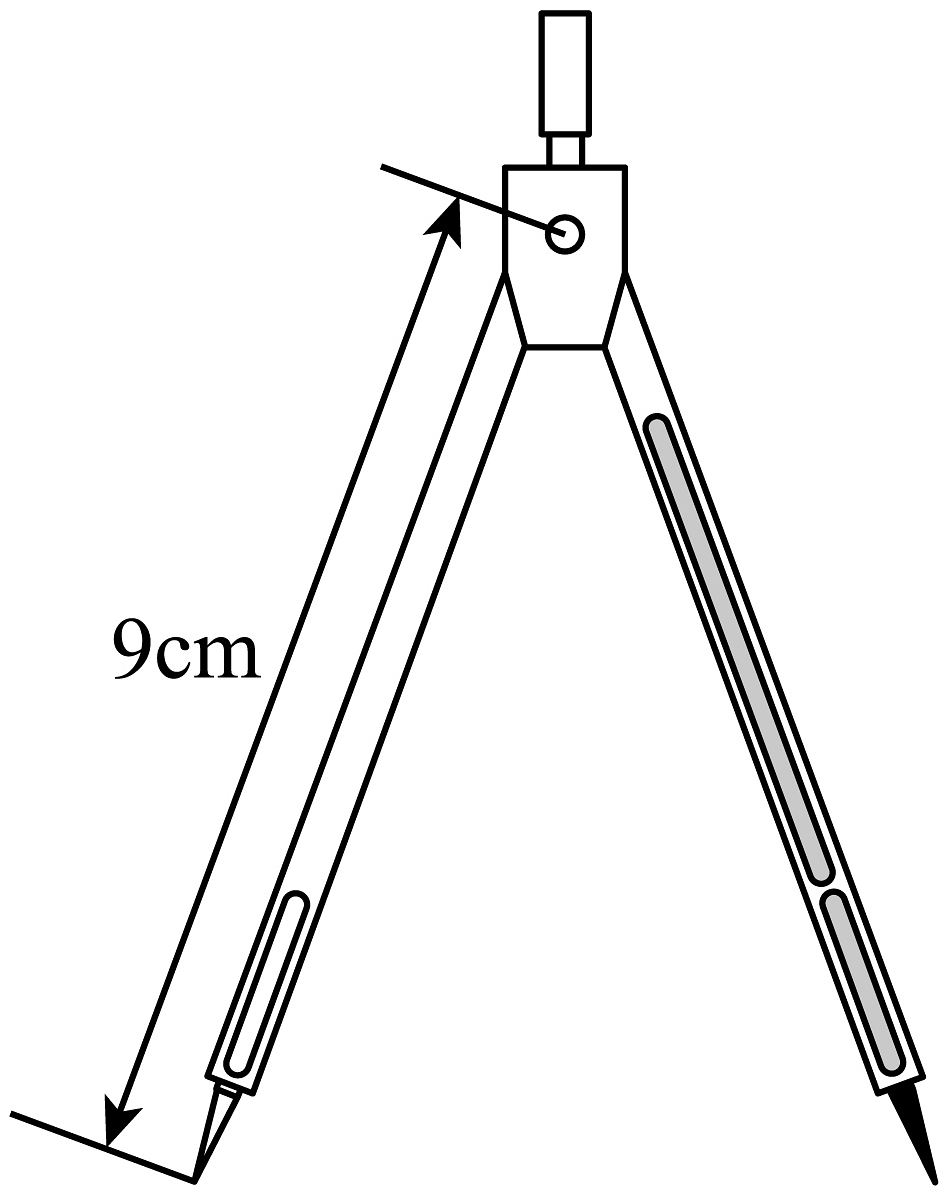 A、 B、 C、 D、
A、 B、 C、 D、 -
7、下列各图中,经过折叠可以得到正方体的是( )A、
 B、
B、 C、
C、 D、
D、
-
8、下表记录的是某一天中四个城市的平均气温,其中气温最低的是( )
北京
哈尔滨
贵阳
重庆
A、北京 B、哈尔滨 C、贵阳 D、重庆 -
9、森林火灾是一种常见的自然灾害,危害很大.随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,区域内是一片森林,有一台救火飞机沿东西方向 , 由点飞向点 , 已知点为其中一个着火点,且点与点 , 的距离分别为和 , 又 , 飞机中心周围以内可以受到洒水影响.
 (1)、求的面积.(2)、着火点能否受到洒水影响?为什么?
(1)、求的面积.(2)、着火点能否受到洒水影响?为什么? -
10、已知一次函数图象y=kx+b经过点A(﹣3,1)和点B(0,﹣2).
(1)求这个一次函数的解析式.
(2)已知点C的纵坐标为﹣3,且在这个一次函数图象上,求△AOC的面积.

-
11、如图,在平行四边形中,已知.
 (1)、作的平分线交于点 , 在上截取 , 连接;(要求:尺规作图,保留作图痕迹,不写作法.)(2)、直接写出四边形的形状.
(1)、作的平分线交于点 , 在上截取 , 连接;(要求:尺规作图,保留作图痕迹,不写作法.)(2)、直接写出四边形的形状. -
12、先化简,再求值: , 其中 , .
-
13、如图,O是矩形的对角线的中点,M是的中点,若 , , 则的长为 .

-
14、【性质探究】
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
【迁移应用】
(3)记△DGO的面积为S1 , △DBF的面积为S2 , 当时,求的值.
【拓展延伸】
(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.

-
15、若关于x的一元二次方程的一个根是3,则a的值为 .
-
16、如图,小茗同学在物理实验操作课中观察光的折射现象,发现水平放置的水杯底部有一束光线从水中射向空气时要发生折射.当入射光线和水杯的底面成 , 折射光线与水杯口平面成时,的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、下列各式计算正确的是( )A、 B、 C、 D、
-
18、以下四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、某数学活动小组设计采用航拍无人机测量楼高.如图所示,航拍无人机飞行到楼房前方某高度时测得楼房底端B处俯角为 , 楼房顶端A处俯角为 , 米.
 (1)、求此时航拍无人机离地面的垂直距离.(2)、求楼房高度 .
(1)、求此时航拍无人机离地面的垂直距离.(2)、求楼房高度 .(本题参考数据: , 结果精确到1米)
-
20、列方程(组)解应用题:重庆某动漫玩具创意企业计划委托供货商生产自己设计的甲、乙两种动漫玩具共7800个投放市场,甲玩具的数量比乙玩具数量的一半少300个.(1)、甲、乙两种动漫玩具的数量分别是多少个?(2)、若供货商安排20人同时生产这两种动漫玩具,每人每天能生产甲玩具20个或乙玩具30个,应分别安排多少人生产甲、乙玩具,才能确保同时完成两种玩具的生产任务?