-
1、 在古代建筑中,榫()卯()结构至关重要,它通过凸出的榫头和凹进的榫眼精密配合连接,使得建筑物连接牢固且难以松动.工匠们制作一种特定的榫卯组合,每个榫头需要耗费的木材比每个榫眼需要耗费的木材多千克.已知用30千克木材制作榫头的数量与用25千克木材制作榫眼的数量相同.设制作1个榫头需要耗费的木材为x千克,则可列方程为( )A、 B、 C、 D、
-
2、 课堂上,老师出示了这样一个问题:如图①,已知 , 请利用尺规作 . 如图②是甲、乙两位同学的作法,其中正确的是( )
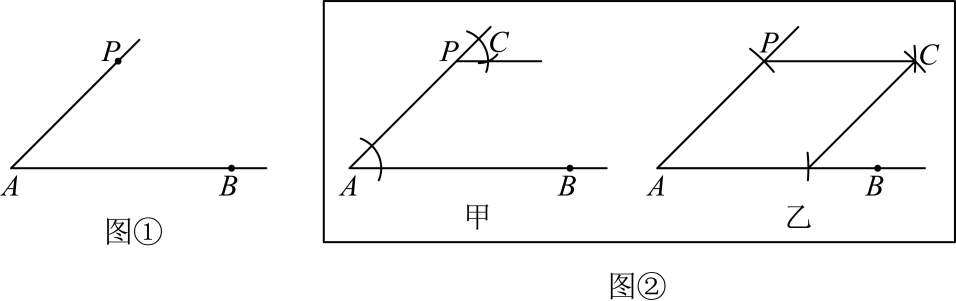 A、甲、乙均正确 B、甲正确,乙错误 C、乙正确,甲错误 D、甲、乙均错误
A、甲、乙均正确 B、甲正确,乙错误 C、乙正确,甲错误 D、甲、乙均错误 -
3、 下列运算正确的是( )A、 B、 C、 D、
-
4、 十二地支是中国传统文化中的一个重要概念,与天干共同构成了干支纪年系统,它们也与十二生肖对应,分别是:子(鼠),丑(牛),寅(虎),卯(兔),辰(龙),巳(蛇),午(马),未(羊),申(猴),酉(鸡),戌(狗),亥(猪).小东购买了一套十二生肖邮票,从中任选一张邮票送给小深,则恰好选中邮票“蛇”的概率是( )A、 B、 C、 D、
-
5、 下列倡导环保的图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、 如图,数轴上点A表示的数的绝对值是( )
 A、 B、 C、3 D、
A、 B、 C、3 D、 -
7、以下列各组数为边长,可以构成直角三角形的是( )A、2,3,4 B、3,4,6 C、6,8,10 D、7,24,26
-
8、综合与探究
小红根据学习轴对称的经验,发现其中线段之间、角之间存在着紧密的联系,他以等腰三角形为背景展开了拓展探究.如图①,在等腰直角三角形中, , , 点D是直线左侧的一动点.作点C关于直线的对称点为点E,连接 , 直线与直线交于点F,连接 , .
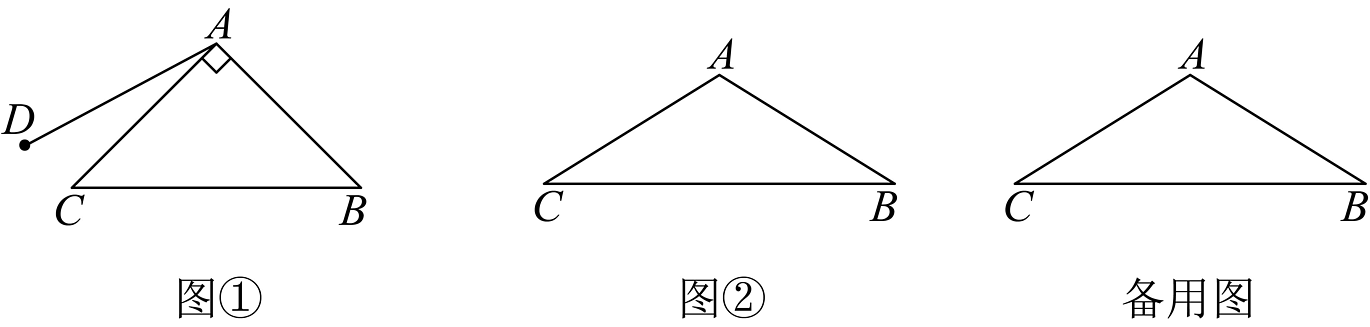
【动手操作】
(1)当时,根据题意,用尺规在图①上画出图形;若 , , 则 ;
【问题探究】
(2)根据(1)所画图形,猜想的大小以及 , , 的数量关系,并说明理由;
【拓展延伸】
(3)如图②,在等腰三角形中, , , 其余条件不变,当时,若 , , 直接写出 , , 的数量关系以及的值.
-
9、再一次校运会上,一名男同学仍铅球时,其运动轨迹为如图所示的一条抛物线,已知仍出铅球时,铅球距离男同学的水平距离长为x(单位:m),距离地面高度为y(单位:m)满足下表关系:.
x
0
1
2
3
4
y
1.4
1.9
2.2
2.3
2.2
 (1)、求出铅球的运动轨迹的解析式;(2)、若铅球落地的沙坑低于水平面 , 沙坑边缘与男同学的距离 , 计算裁判员测量的铅球落地位置G到F的距离;(3)、为了使铅球抛出距离更远,该男同学计划让铅球扔出后,达到的最大高度在B的下方米处,试计算说明,该男同学的抛出的铅球距离是增大还是减少?增大(或减少)多少.
(1)、求出铅球的运动轨迹的解析式;(2)、若铅球落地的沙坑低于水平面 , 沙坑边缘与男同学的距离 , 计算裁判员测量的铅球落地位置G到F的距离;(3)、为了使铅球抛出距离更远,该男同学计划让铅球扔出后,达到的最大高度在B的下方米处,试计算说明,该男同学的抛出的铅球距离是增大还是减少?增大(或减少)多少. -
10、如图,点A、B、C分别是○O上的三点,连接交线段于点D.
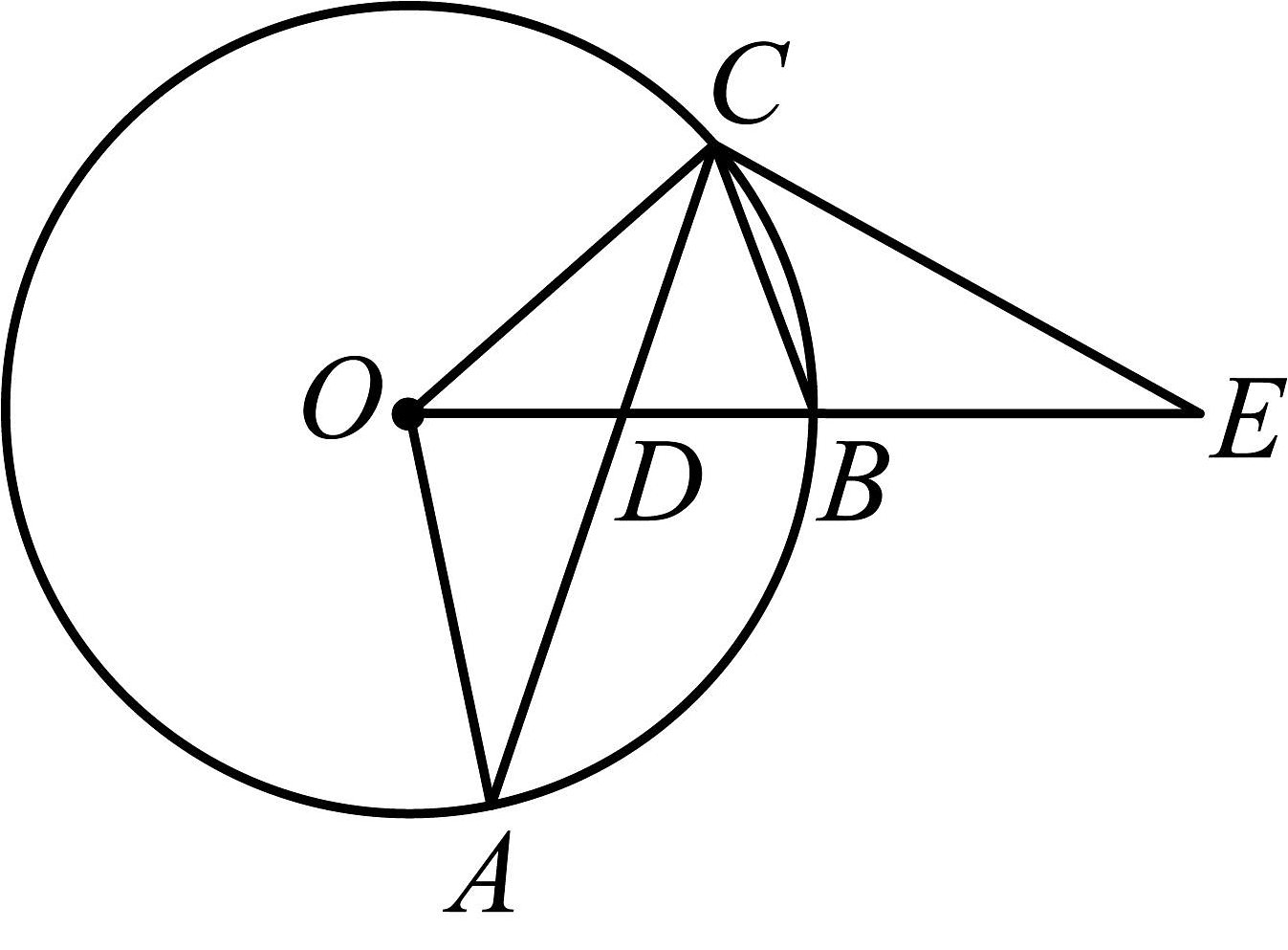 (1)、若 , 则 ;(2)、若D是的中点,延长至点E,使得 , 连接 , 求证;(3)、在(2)的条件下,若 , , 求的长.
(1)、若 , 则 ;(2)、若D是的中点,延长至点E,使得 , 连接 , 求证;(3)、在(2)的条件下,若 , , 求的长. -
11、贵州是一个多桥梁的省份,如图 1 是全球最高的桥——北盘江大桥.现某数学兴趣小组打算利用所学的数学知识测量它的桥长和桥高.数学小组的同学们绘制出了如图 2 的几何图形:为桥面, , 为两个桥墩在桥上方的部分,满足且 . C为桥下方的最低点.同学们在 B点处用测角仪测出了F的仰角为 , G的仰角为 , C的俯角为 , 从 A点又测得 C的俯角为 .
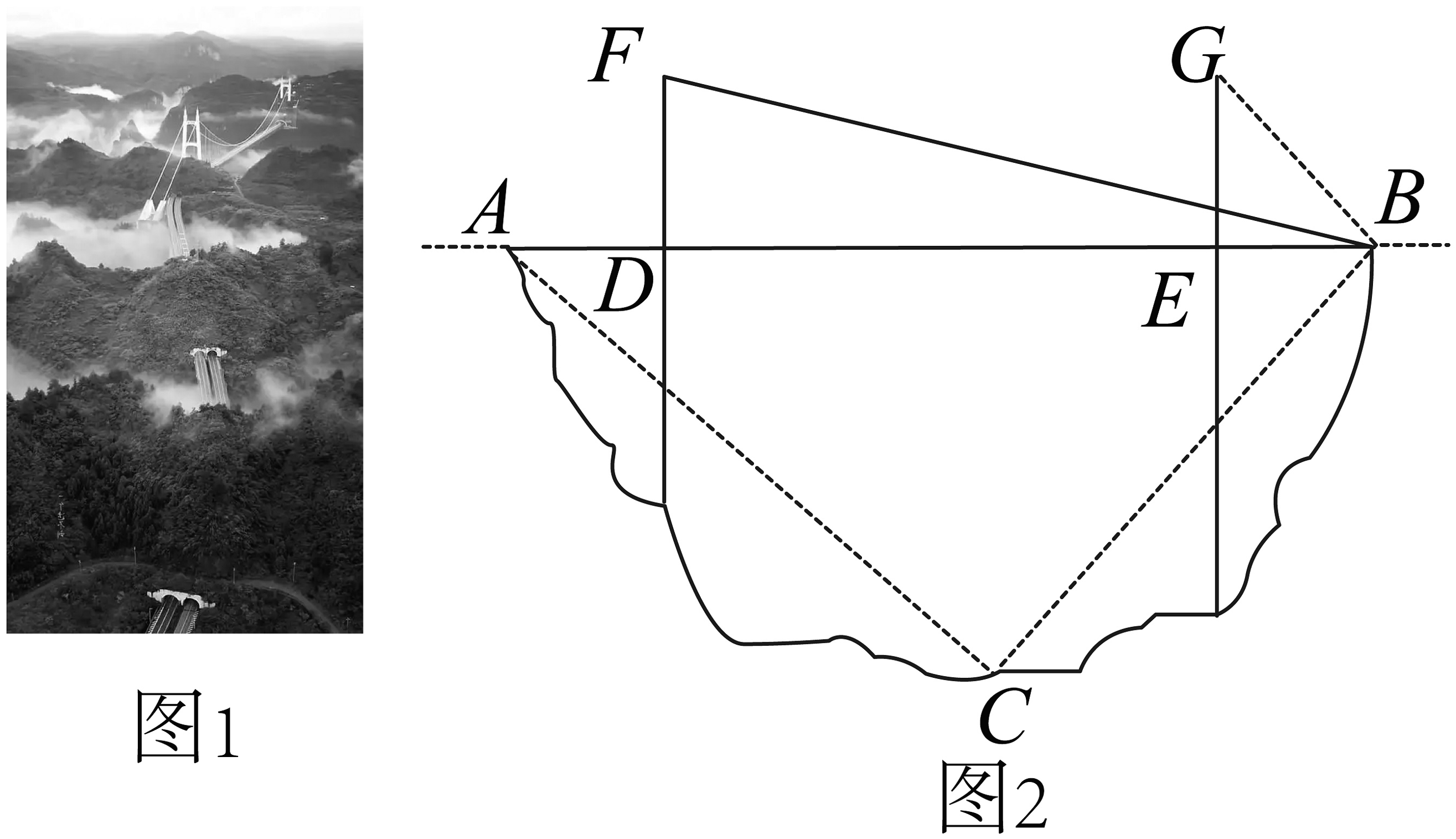 (1)、桥面 的长为 ;(结果保留整数,参考数据: , ,
(1)、桥面 的长为 ;(结果保留整数,参考数据: , ,)
(2)、请计算 C点到桥面的距离.(结果保留整数,参考数据: , , , , , ) -
12、推动绿色发展,促进人与自然和谐共生,某地区政府牢记习总书记“绿水青山就是金山银山”嘱托,鼓励村民牢记生态发展的同时,“甩开膀子加油干”积极脱贫致富,该地区政府购进了甲、乙两种果苗分发给村民,已知第一批果苗共1.2万株;第一批果苗分发后,发现村民种植果苗热情很高,于是该区政府决定购进第二批果苗,已知第二批甲种果苗的数量比第一批多 , 第二批乙种果苗比第一批多 , 且第二批果苗总数为万株.(1)、分别求出第一批两种树苗各多少株;(2)、市场调研发现,甲种果苗每株售价3元,乙种果苗每株售价2元,该区政府计划明年拿出不高于4.8万元购进两种果苗2万株,则最多购买甲种果苗多少株?
-
13、已知反比例函数()与正比例函数交于、两点,且点坐标为;
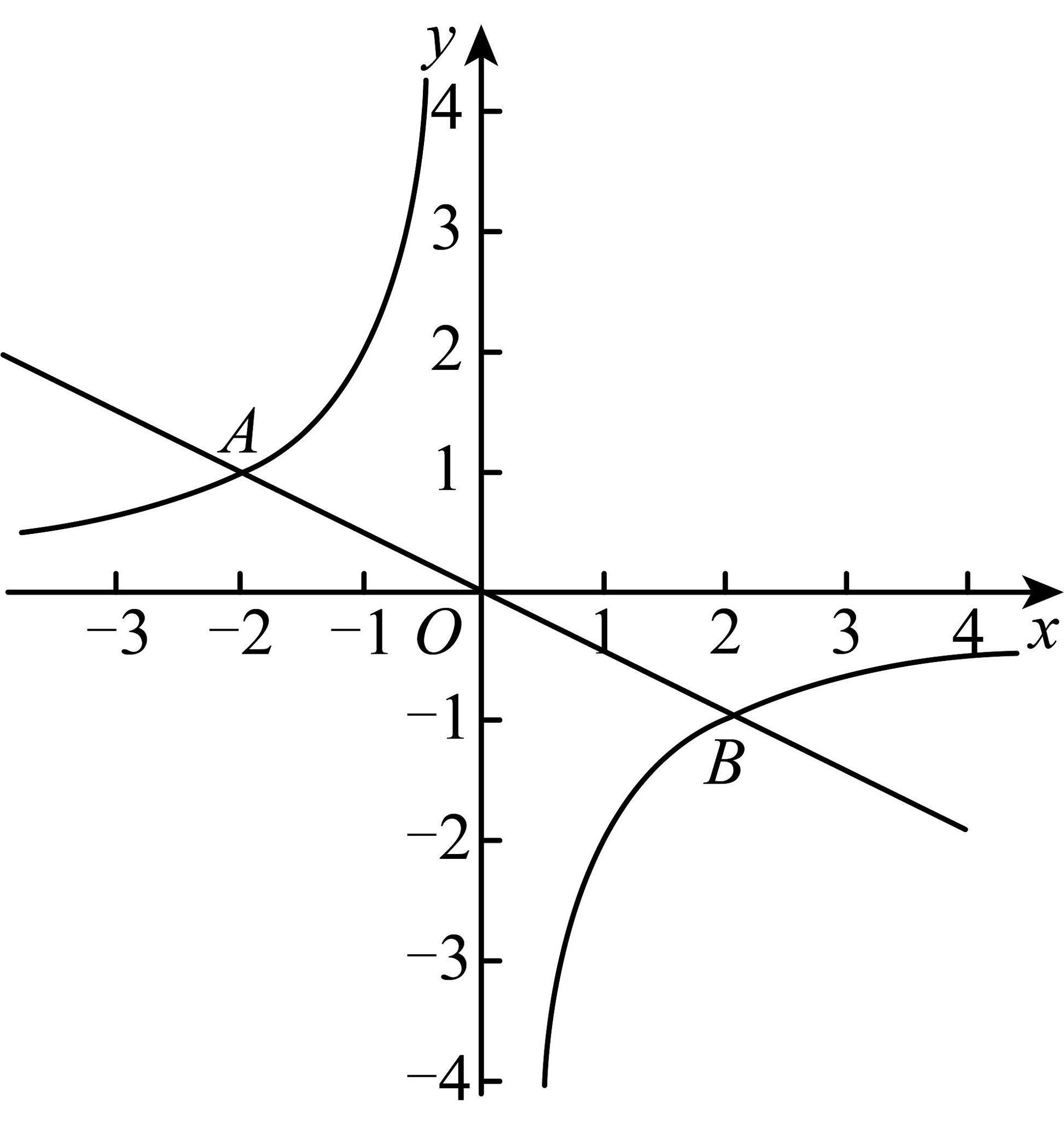 (1)、求、的值;(2)、直线与一次函数的图象相交于点 , 与反比例函数的图象相交于点 , 若 , 结合函数图象,直接写出的取值范围: .
(1)、求、的值;(2)、直线与一次函数的图象相交于点 , 与反比例函数的图象相交于点 , 若 , 结合函数图象,直接写出的取值范围: . -
14、全民阅读有助于提升一个国家、一个民族的精神力量.4月23日,正值第30个“世界读书日”.在贵阳地铁3号线花果园站厅内,“共沐书香签动你我”闲置图书置换活动吸引了众多市民的目光.这一活动通过创新的形式,将书香融入城市文化生活,为市民带来了一场别开生面的文化体验.

某校“综合与实践”小组为了解全校1200名学生的读书情况,随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):
××中学学生读书情况调查报告
调查主题
××中学学生读书情况
调查方式
抽样调查
调查对象
××中学学生
数据的收集、
整理与描述
第一项
您平均每周阅读课外书的时间大约是(只能单选,每项含最小值,不含最大值)
A.8小时及以上;
B.6~8小时;
C.4~6小时;
D.0~4小时.

第二项
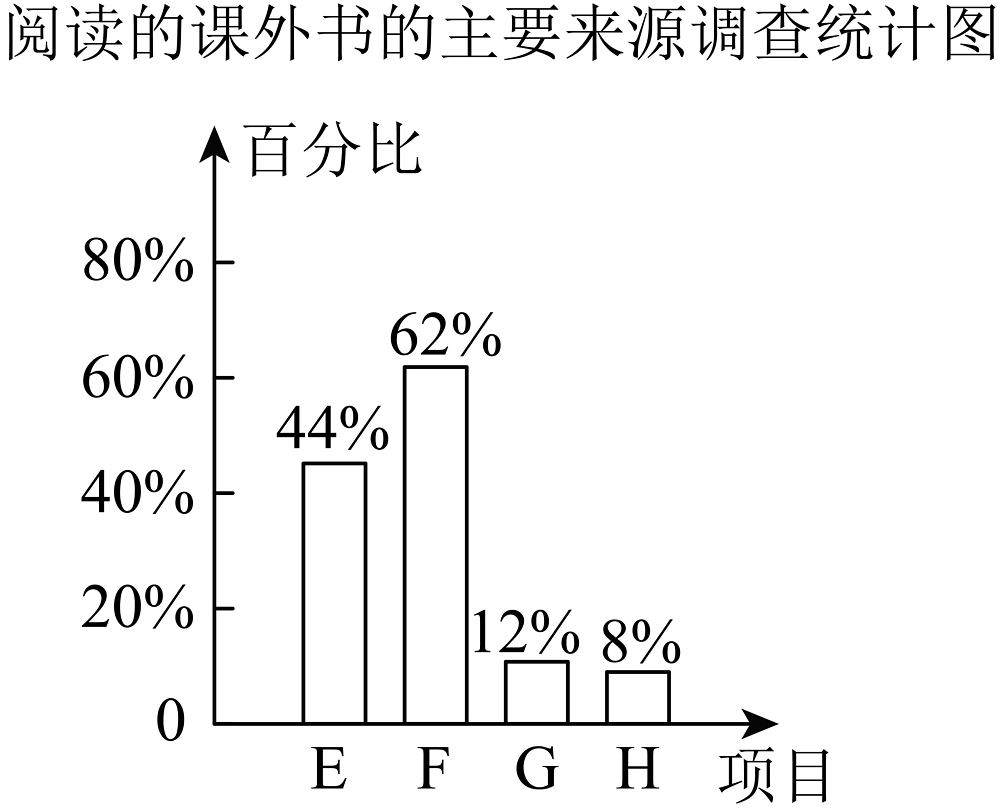
您阅读的课外书的主要来源是(可多选)
E.自行购买;
F.从图书馆借阅;
G.免费数字阅读;
H.向他人借阅.
调查结论
……
请根据以上调查报告,解答下列问题:
(1)、参与本次抽样调查的学生人数为;这些学生中选择“免费数字阅读”的人数;(2)、估计该校1200名学生中,平均每周阅读课外书时间在“6小时及以上”的人数;(3)、该小组要根据以上调查报告在全班进行交流,假如你是小组成员,请结合以上两项调查数据分别写出一条你获取的信息. -
15、七年级2班数学兴趣小组制作了如图所示的“角平分线仪”,小明将角平分线仪的各点表上字母,如图所示,并提出了一个问题:如何证明是的平分线呢?
小丽想,先证明 , 即可得出结论,于是她写出了如下证明过程:
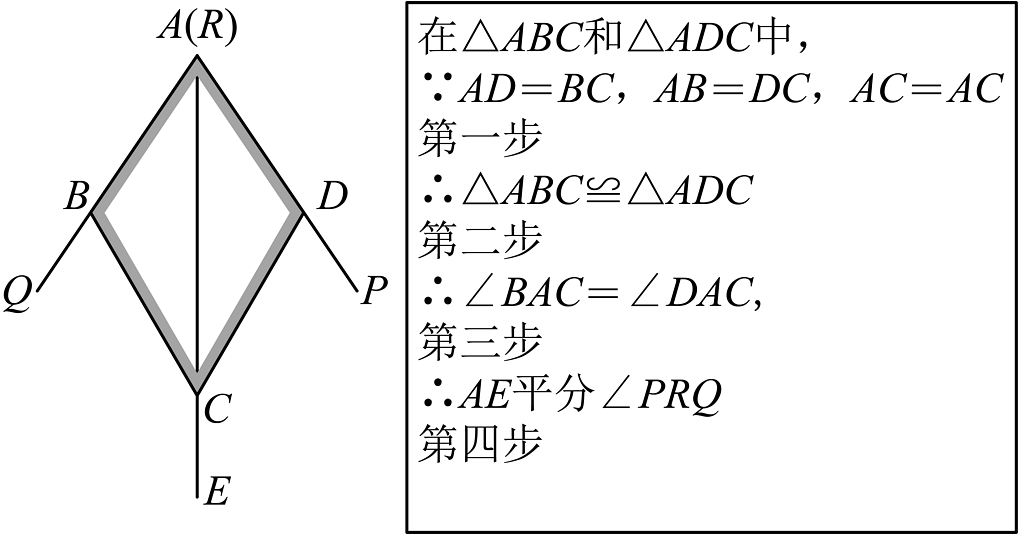
回答下列问题:
(1)、小丽的证明过程从第 步开始出错,第三步的依据是 ;(2)、请你帮助小明写出正确的证明过程. -
16、(1)计算:
(2)化简:
-
17、如图,在中, , 为边上的中线,于点E,连接并延长交点F.已知 , 则的长为 .
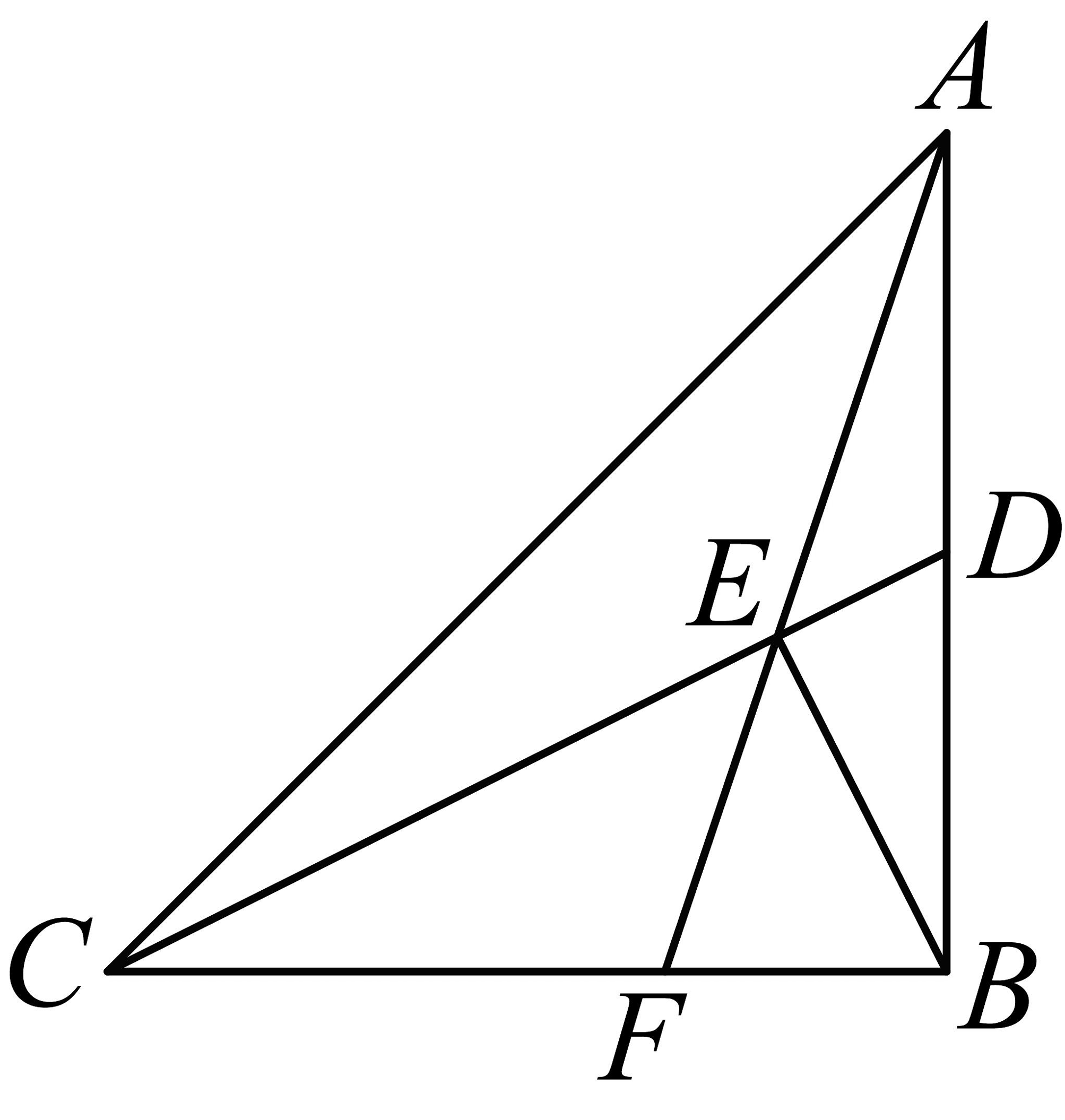
-
18、在一次活动课上,老师拿来一个不透明的袋子,对学生说:里面只有红球和白球,它们除颜色外没有其他区别,已知白球有个,你能估算出红球的数量吗?小聪与他的小组成员设计了如下方案:先摸出一个小球,记录下颜色后放回,摇均匀后再摸一个小球,记下颜色,如此反复,他们记录表格如下:
摸球次数
摸到红球次数
请你根据小聪小组记录数据,估算红球的个数 .
-
19、如图,在等腰中, , 分别以A、B为圆心,大于长为半径画弧,交于点D,连接交于点E,则 .

-
20、若公共汽车上车人数记为“+”,下车人数记为“-” ,一辆公共汽车原有18名乘客,经过某一站时,乘客变化为: , , 这时车上乘客人数为 .