-
1、已知点 , , 都在反比例函数上,则 , , 的大小关系是( )A、 B、 C、 D、
-
2、对于实数a、b,规定一种运算“*”: , 那么不等式组的解在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、
-
3、如图,在正方形网格图中,△ABC与△A'B'C'是位似图形,则位似中心是( )
 A、点R B、点P C、点Q D、点O
A、点R B、点P C、点Q D、点O -
4、体育中考某班6名同学1分钟跳绳成绩(单位:次)分别是178,150,193,181,166,180,这组数据的中位数是( )A、178 B、179 C、181 D、180
-
5、下列计算正确的是( )A、 B、 C、 D、
-
6、第六代战斗机是一种人工智能控制的吸气式超高音速战斗机,此类战机速度预计可以突破5马赫,飞行一小时的距离约为22100km,将数据22100用科学记数法表示时,正确的是( )A、 B、 C、 D、
-
7、在我国,鼓是精神的象征,舞是力量的表现,先贤孔子曾说过“鼓之舞之”,可见“鼓舞”一词起源之早,如图是鼓的立体图形,该立体图形的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
8、下列各数中,2025的相反数是( )A、2025 B、-2025 C、 D、
-
9、如图,AB为O0的弦,点C在弧AB上,AB平分∠OBC,过点C作CE⊥OA于点E,交AB于点F,连结OF.
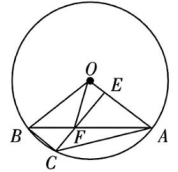 (1)、求证:.(2)、求的值.(3)、当时,判断的形状,并说明理由.
(1)、求证:.(2)、求的值.(3)、当时,判断的形状,并说明理由. -
10、【综合与实践】某兴趣小组开展综合实践活动:在中, , D为AC上一点, , 动点P以每秒1个单位的速度从C点出发,在三角形边上沿匀速运动,到达点A时停止,以DP为边作正方形DPEF.设点P的运动时间为t,正方形DPEF的面积为S,探究S与t的关系.
 (1)、初步感知:如图1,当点P由点C运动到点B时,①当时,.②S关于t的函数解析式为.(2)、当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象.请根据图象信息,求S关于t的函数解析式及线段AB的长.(3)、延伸探究:若存在3个时刻)对应的正方形DPEF的面积均相等.
(1)、初步感知:如图1,当点P由点C运动到点B时,①当时,.②S关于t的函数解析式为.(2)、当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象.请根据图象信息,求S关于t的函数解析式及线段AB的长.(3)、延伸探究:若存在3个时刻)对应的正方形DPEF的面积均相等.① ;
②当时,求正方形DPEF的面积. -
11、图1,图2分别是某型号拉杆箱的实物图与平面示意图,具体信息如下:水平滑杆DE、箱长BC、拉杆AB的长度都相等,即DE=BC=AB,点B,F在线段AC
上,点C在DE上,支撑点F到箱底C的距离FC=32cm,CE:CD=1:5,DF⊥AC于点F,∠DCF=50°,请根据以上信息,解决下列问题:
 (1)、求水平滑杆DE的长度;(2)、求拉杆端点A到水平滑杆DE的距离h的值(结果保留到1cm).(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
(1)、求水平滑杆DE的长度;(2)、求拉杆端点A到水平滑杆DE的距离h的值(结果保留到1cm).(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19). -
12、某校为了解该校学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
 (1)、这次考察中一共调查了名学生:“排球”部分所对应的圆心角为度.(2)、补全条形统计图.(3)、若全校有3000名学生,试估计该校喜欢乒乓球的学生约有多少人?
(1)、这次考察中一共调查了名学生:“排球”部分所对应的圆心角为度.(2)、补全条形统计图.(3)、若全校有3000名学生,试估计该校喜欢乒乓球的学生约有多少人? -
13、小乐和小嘉同时从学校出发,分别骑自行车沿同一条路线到体育馆进行锻炼,图中折线O-A-B-C和线段OD分别表示小乐和小嘉离学校的距离y(米)与时间x(分钟)的函数关系的图象,且两人骑车速度均保持不变,根据图中信息,解答下列问题:
 (1)、求出小嘉离学校的距离)(米)与时间x(分钟)的函数表达式,并直接写出图中a的值.(2)、出发后经过15分钟,小乐和小嘉相距多少米?
(1)、求出小嘉离学校的距离)(米)与时间x(分钟)的函数表达式,并直接写出图中a的值.(2)、出发后经过15分钟,小乐和小嘉相距多少米? -
14、解方程组:
-
15、计算:.
-
16、一段圆弧形公路弯道的半径为200m,圆心角为18°,则该弯道的长度为m(结果保留π).
-
17、不等式2x-1的解集是.
-
18、如图,已知AB为⊙O的直径,弦AC,BD相交于点E,M在AE上,连结DM.若AB=1,∠DMC=∠B,则cos∠AED的值始终等于线段长( )
 A、DM B、EM C、AM D、CM
A、DM B、EM C、AM D、CM -
19、已知点 , 为二次函数图象上的两点(不为顶点),则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
20、甲、乙两组同学在植树活动中均植树120棵,已知甲组每小时比乙组多种10棵,且甲组比乙组提前2小时完成.设乙组每小时植树x棵,可列方程为( )A、 B、 C、 D、