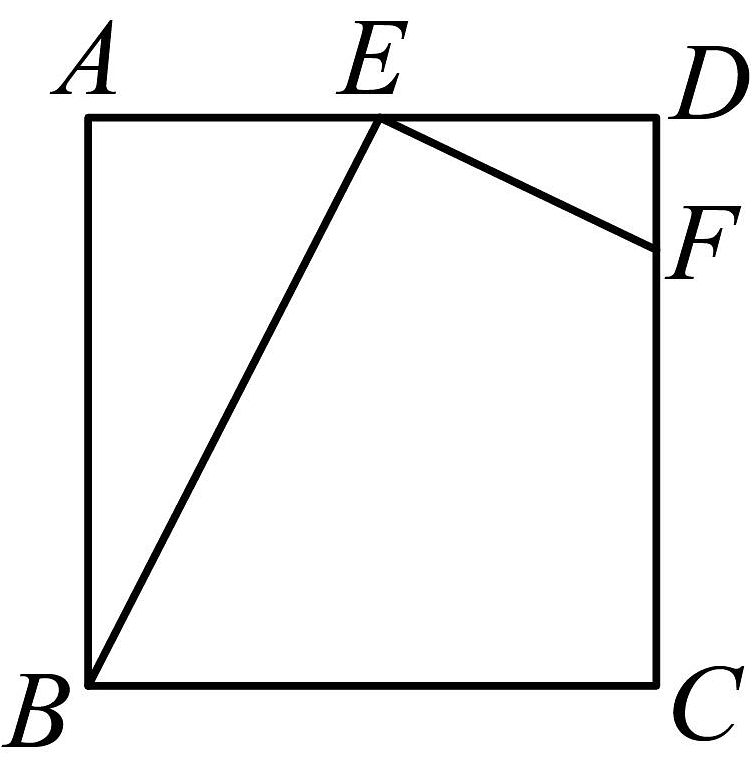
-
1、如图，在正方形ABCD中，点E是AD的中点，点F在CD上，且 ， 连接EF、BE．求证：∽
-
2、解不等式组：
-
3、如图，正方形ABCD的边长为 ， E，F分别是BC，CD的中点，连接AE，G为AE上的一点，且∠F GE=45°，则GF的长为 ．
-
4、已知函数y＝x2﹣2ax+7，当x≤3时，函数值随x增大而减小，且对任意的1≤x1≤a+2和1≤x2≤a+2，x1 ， x2相应的函数值y1 ， y2总满足|y1﹣y2|≤9，则实数a的取值范围是（ ）A、﹣3≤a≤4 B、﹣3≤a≤5 C、3≤a≤4 D、3≤a≤5
-
5、如图，是一台笔记本电脑，屏幕与键盘所成夹角为110°，若屏幕的长度为 ， 则上方边界处到桌面的距离为（ ）
A、 B、 C、 D、 -
6、某文具超市有A，B，C，D四种笔记本销售，它们的单价分别是5元，4元，3元，6元，某天的笔记本销售情况如图所示，那么这天该文具超市销售的笔记本的单价的平均值是（ ）
A、3元 B、4元 C、4.2元 D、4.5元 -
7、如图，CD为⊙O的直径，在线段OC上取一点P，过点P作AB⊥OC（点A在直径CD上方），连结AC、DB并延长交于点F，过点A作AE⊥BD于点E，交直径CD于点G.
(1)、求证：CP=PG.(2)、设∠BAE=α，∠F=β.求B关于α的函数关系式.(3)、当OG=OP时，求tanα·tanβ的值. -
8、已知二次函数y=x2-3x-m2+3m（m≠0的实数）.(1)、二次函数图象的对称轴是.(2)、当m=2时，
①若将平面内一点A（1，n）向右平移3a个单位，则与抛物线上的点B重合；向左平移2a个单位，则与抛物线上的点C重合，求n的值.
②如果点p（x，y）在抛物线上，且到y轴的距离小于等于2，那么我们称点p是y轴的“亲密点”，求所有“亲密点”的y的取值范围.
(3)、对于二次函数图象上的两点 ， ， 当 ， 时，均满足 ， 直接写出t的取值范围. -
9、为了响应国家提倡的“节能环保”号召，某公司小金、小衢两位员工每天骑共享单车上班（每次骑行均按平均速度行驶，其他因素忽略不计），每次支付费用y元与骑行时间xmin之间的对应关系如图所示，其中A种共享单车支付费用对应的函数为y1；B种共享单车支付费用是10min之内，起步价6元，对应的函数为y2.请根据函数图象信息，解决下列问题：
(1)、小金每天早上骑行A种共享单车或B种共享单车去公司上班，已知两种共享单车的平均行驶速度均为300m/min，小金家到公司的距离为9000m，那么小金选择种电动车更省钱（填“A”或“B”）.(2)、当x>10时，求A、B两种共享单车的支付费用的函数表达式.(3)、一天，小金骑行A种共享单车从家到公司上班，小衢骑行B种共享单车从家到公司上班，若两人支付费用同为7.6元，求小金和小衢骑行的时间差. -
10、小丽与小明，小颖同学一起研究一个利用尺规作一个30°角的问题：
如图1，已知在射线AX上，依次取点B，C，使BC=AB.
小明：如图2，分别以A，C为圆心，AC长为半径画弧，交于点D，连结AD，BD，则∠ADB=30°.
小丽：如图3，分别以A，B为圆心，AB长为半径画弧，交于点D，连结CD，则∠ACD=30°.
小颖：如图4，分别以A，C为圆心，大于AB长为半径画弧，交于点D；以B为圆心，AB长为半径画弧交射线BD于点E；以E为圆心，BE长为半径画弧交弧AE于点F，连结BF，则∠ABF=30°.
(1)、做法正确的同学有.(2)、请选择你认为正确的一种做法给出证明.证明：我选择证明图 ▲ （填序号）
-
11、某芯片制造厂为了提高产品优良率，对一批新生产的芯片进行抽样测试，测试工程师随机抽取了m片芯片，记录每片芯片的最高稳定运行频率（单位：GHz），将数据整理并绘制成如图表，根据行业标准，运行频率f≥3.0GHz的芯片被视为合格品，可用于高端计算设备；而运行频率f＜3.0GHz的芯片需降级使用或返工。
运行频率的频数分布表
运行频率区间fIGHz
频数（芯片片数）
2.0≤f<2.5
7
2.5≤f<3.0
a
3.0≤f<3.5
15
3.5≤f<4.0
b
4.0≤f＜4.5
40
(1)、m= ， n=.(2)、在扇形统计图中，运行频率为3.5≤f<4.0的扇形的圆心角度数是.(3)、若该批次共生产了5000片芯片，估计整批芯片中合格品的数量. -
12、如图，在△ABC中，∠ABC=135°，AD是BC边上的高线，△ABC的面积为6，BC=2.
(1)、求AB的长.(2)、求cos∠ACB的值. -
13、解方程组：
-
14、计算：
-
15、如图，在菱形ABCD中，对角线AC，BD相交于点O，线段AD与A'D'关于过点O的直线1对称，点D的对应点D'在线段OC上，A'D'与BC交与点G，将△AEF沿EF折叠，点A与点D'重合，且D'F平分∠AD'A'，则DE：CG=.
-
16、如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为.
-
17、如图，经过A，B两点的⊙0与AC相切于点A，与边BC相交于点E，AD为⊙0的直径，AB=AC，连结DE，若∠C=36°，则∠BED的度数为.
-
18、古语有言“逸一时，误一世”，其意是教导我们要珍惜时光，切勿浪费时间，浪费青春，其数字谐音为“114514”，在这一组数中随机选择一个数字，选到数字“4”的概率为.
-
19、如图，在△ABC中，点D是AB上一点（不与点A，B重合），过点D作DE//BC交AC于点E，过点E作EF//AB交BC于点F，点G是线段DE上一点，EG=2DG，点H是线段CF上一点，CH=2HF，连接AG，AH，GH，HE.若已知△AGH的面积，则一定能求出（ ）
A、△ABC的面积 B、△ADG的面积 C、四边形DBFE的面积 D、△EFC的面积 -
20、赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形ABCD，中间是一个小正方形EFGH，连接DE与FG相交于点M，延长DE交BC于点N，若M是DE的中点， ， 则EN的长（ ）
A、 B、 C、2 D、