-
1、如图,下列条件中能判定AB∥CD的是( )

①DAC=BCA; ②BAC=ACD;
③B=D; ④EAB=DCF
A、② B、B.②③④ C、②④ D、①③ -
2、科学家在研究某种新型细胞时,测量出该细胞的直径约为米,数据用科学记数法表示为( )A、 B、 C、 D、
-
3、下列方程中,是二元一次方程的是( )A、xy=1-y B、x+2y=3x-2 C、3x-1=2 D、x+1=2-
-
4、在平面直角坐标系中,已知抛物线 , 设抛物线的对称轴为点 , 是抛物线上两个点,当时,对的每一个值,总存在 , 使得 , , 且成立,则的取值范围为 .
-
5、一个几何体如图水平放置,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
6、2025是春意盎然,生机勃勃的双春年,2025的倒数是( )A、 B、2025 C、 D、
-
7、如图,弦 , 相交于点P, .
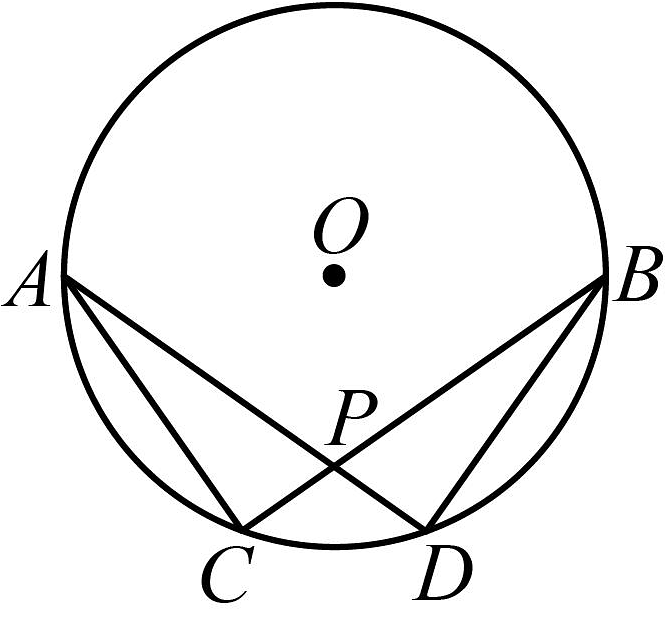 (1)、求证:;(2)、若连接恰是的直径,且 , 则 .
(1)、求证:;(2)、若连接恰是的直径,且 , 则 . -
8、如图,在中, , 是的中点, , 垂足为 .
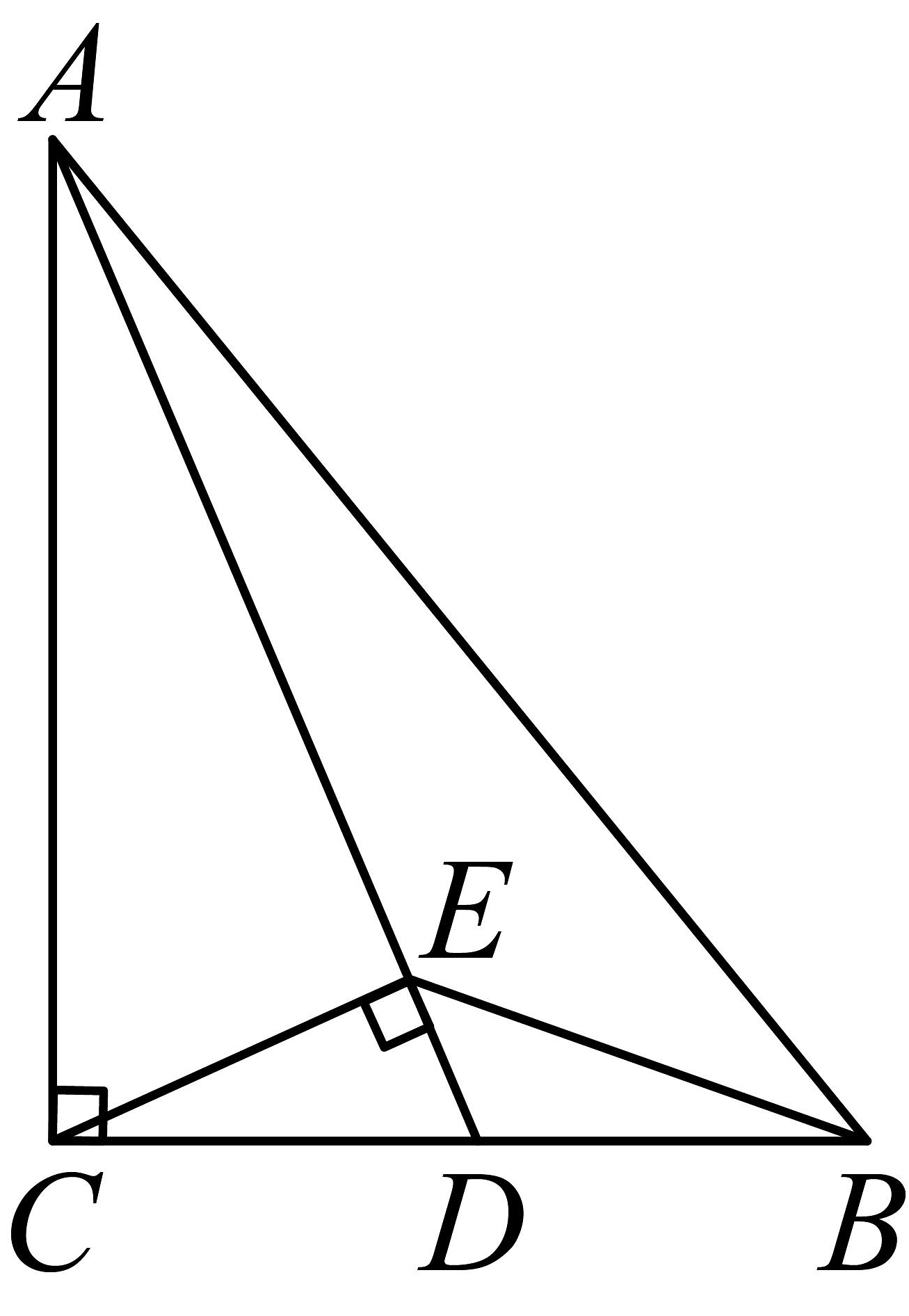 (1)、证明:;(2)、证明: .
(1)、证明:;(2)、证明: . -
9、已知直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 试求的度数.

-
10、因式分解:(1)、;(2)、
-
11、在平面直角坐标系中,已知点 , 点 , 则直线与(填“x”或“y”)轴平行.
-
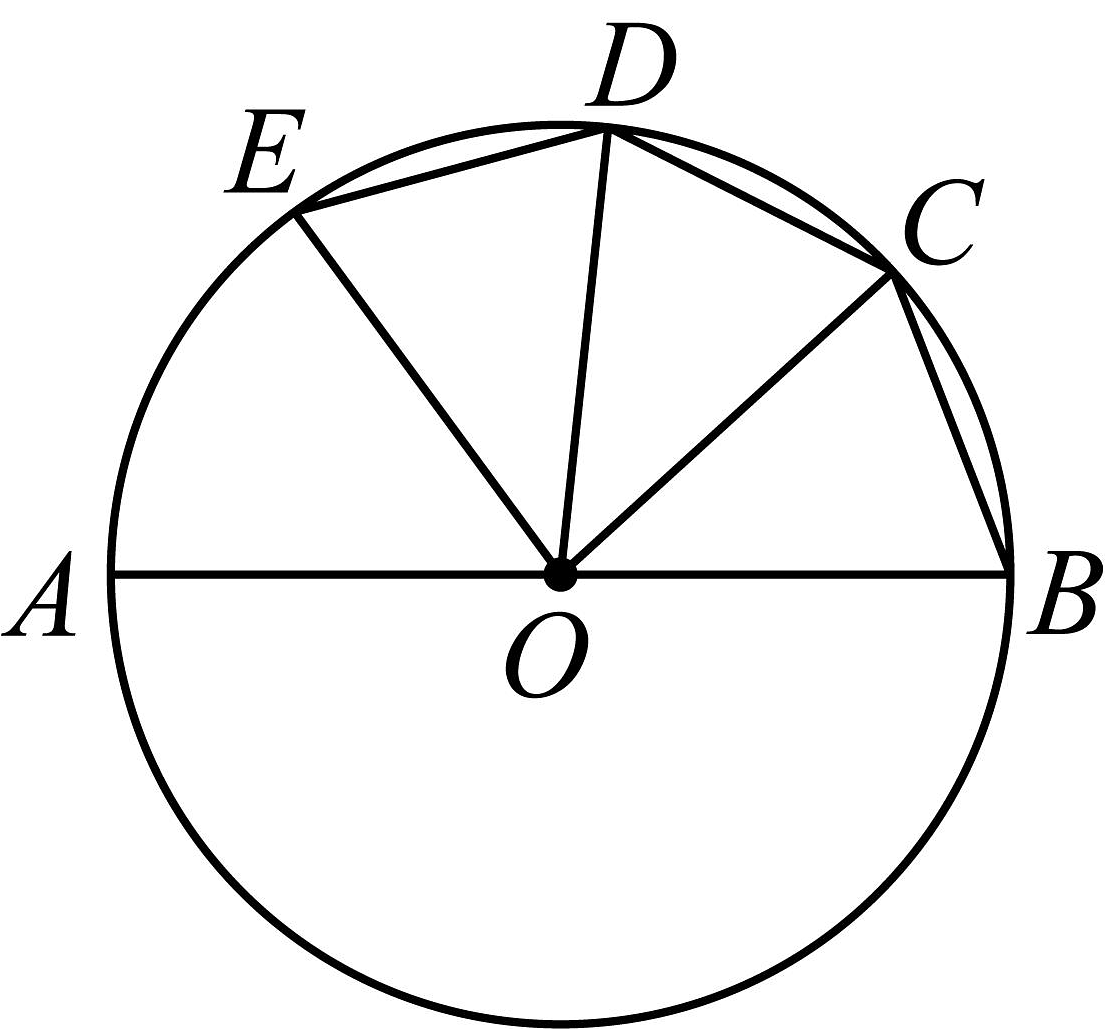
12、如图,已知是的直径, , , 那么弧度数等于 .
-
13、若 , 互为相反数, , 互为倒数,则 .
-
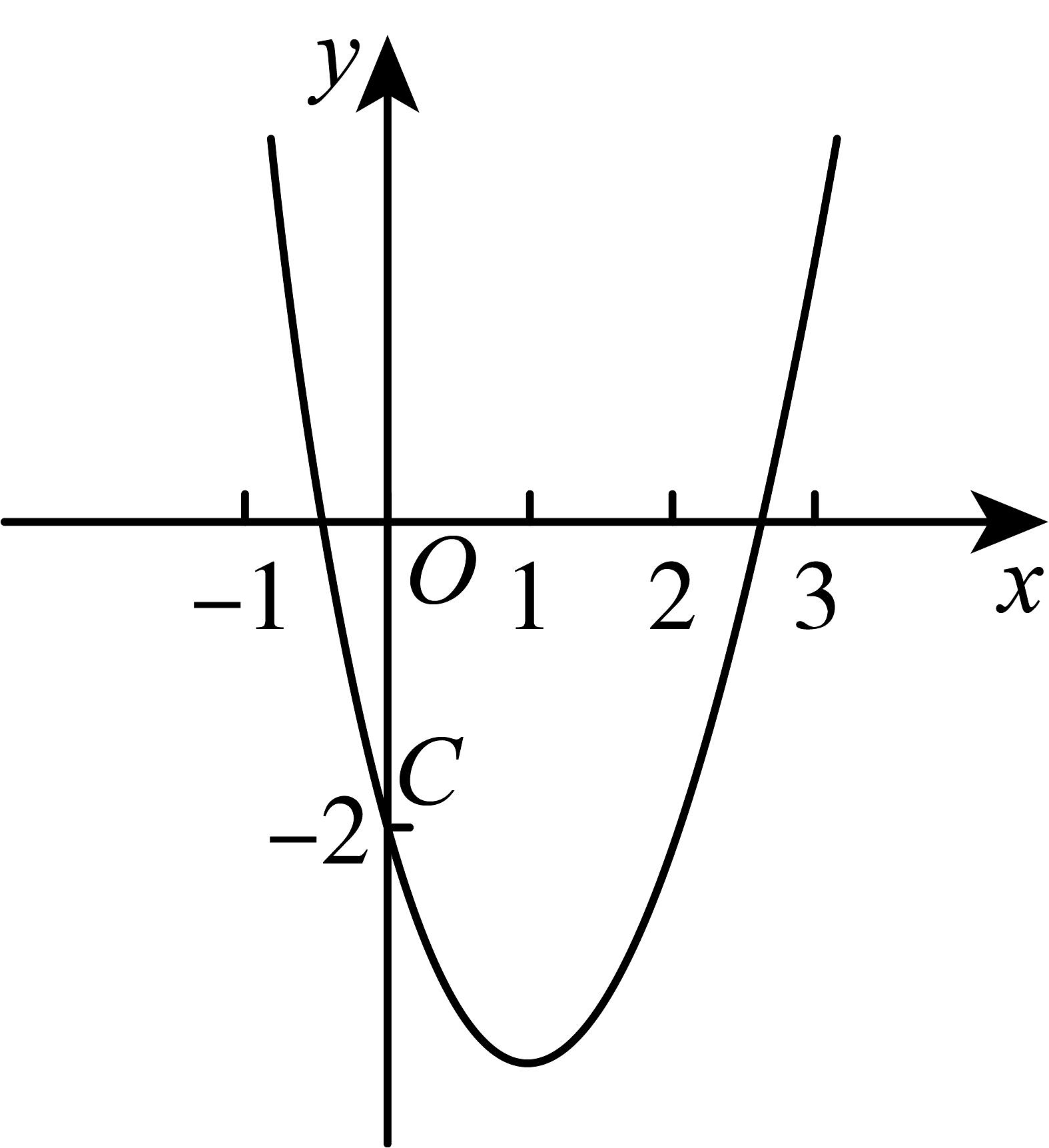
14、如图,已知抛物线过点与x轴交点的横坐标分别为 , , 且 , , 则下列结论:
①;
②方程有两个不相等的实数根;
③;
④;
⑤ . 其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
15、如图,在平面直角坐标系中,四边形为矩形,点 , 分别在轴、轴上,且点 , 为边上一点,将沿所在直线翻折,当点的对应点恰好落在对角线上时,点的坐标为( )
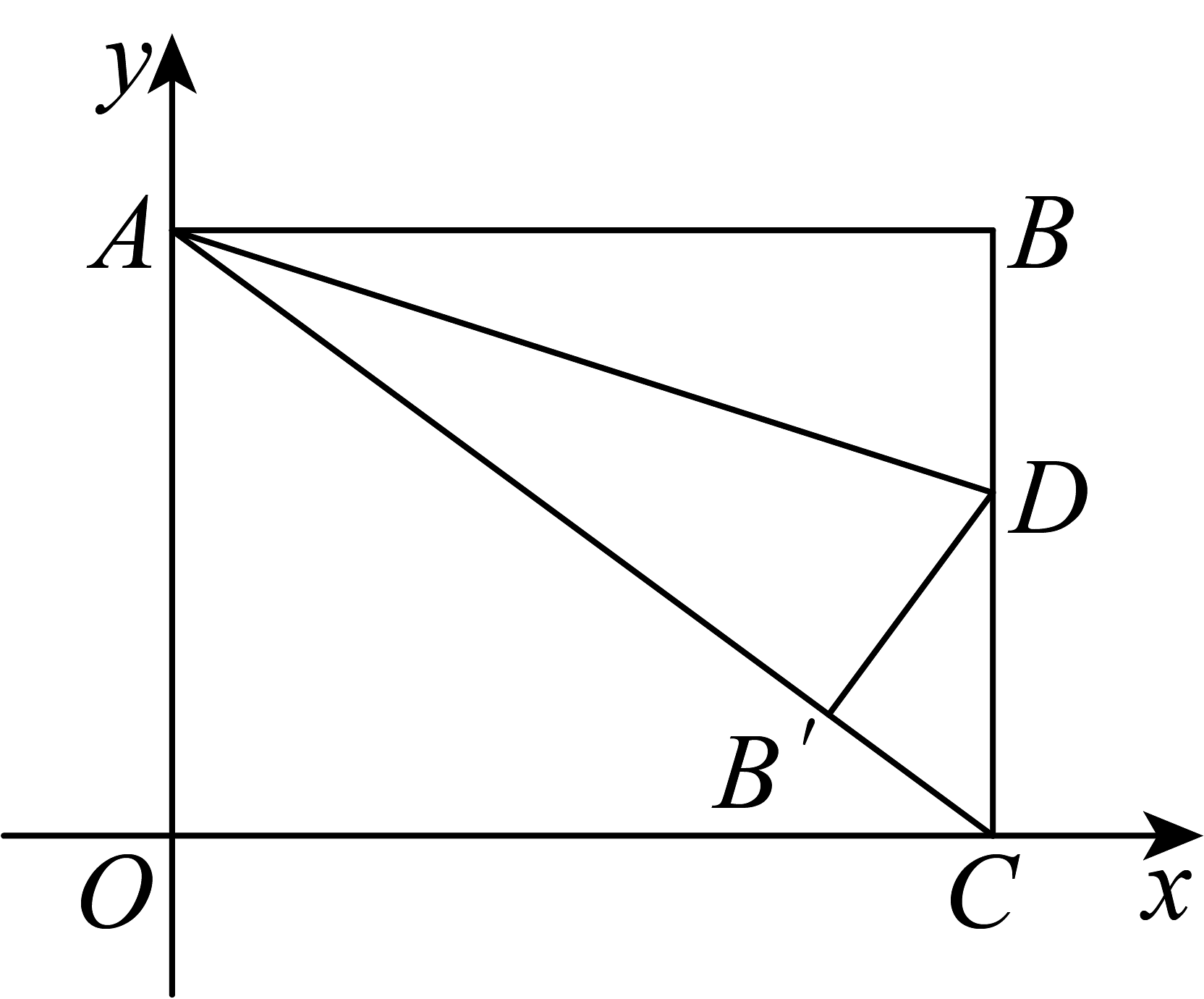 A、 B、 C、 D、
A、 B、 C、 D、 -
16、按一定规律排列的单项式: . 则第7个单项式是( )A、 B、 C、 D、
-
17、下列调查样本中最适合用普查的是( )A、了解一批电视机的使用寿命 B、了解我市居民的年人均收入 C、了解我市学生的视力情况 D、了解某校学生的课外阅读情况
-
18、已知 , 求代数式的值.
-
19、如图,已知 , , D为上一点,构造菱形 , 点E在线段上,G为上一点, , 连接交于点H.
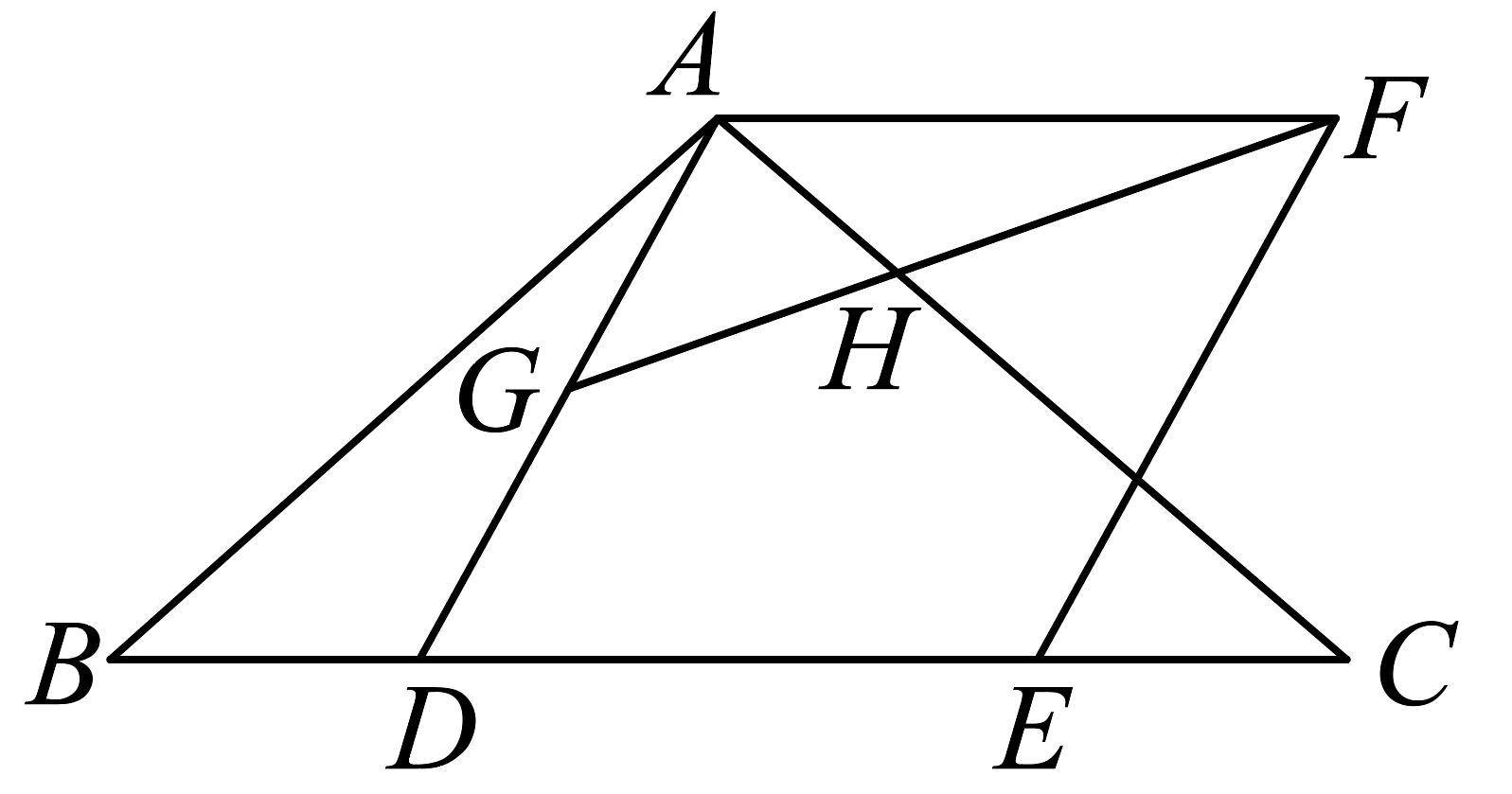 (1)、求证: .(2)、当G为的中点, , 时,求的长.(3)、若 , 求证: .
(1)、求证: .(2)、当G为的中点, , 时,求的长.(3)、若 , 求证: . -
20、如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处保持的速度匀速运动.小聪测量黑球减速后运动距离(单位:cm)随运动时间(单位:s)变化的数据,整理得下表.

运动时间
0
1
2
3
4
…
运动距离
0
14
24
…
探究发现,与之间的数量关系可以用二次函数来描述.
(1)、求关于的函数关系式.(2)、当时,求两球之间的距离.(3)、黑球能否追上白球?若能,求出追上时的值;若不能,求出它们之间的最短距离.