相关试卷

1、某校为七年级学生提供了“科学实验”“趣味棋艺”，“喵历史”，“时光合唱”四种课后服务项目，为了解学生最喜欢哪个项目，随机抽取了该校七年级部分学生进行调查，根据调查结果，绘制了如下两幅尚不完整的统计表和扇形统计图，请你根据统计图提供的信息，解答下列问题：

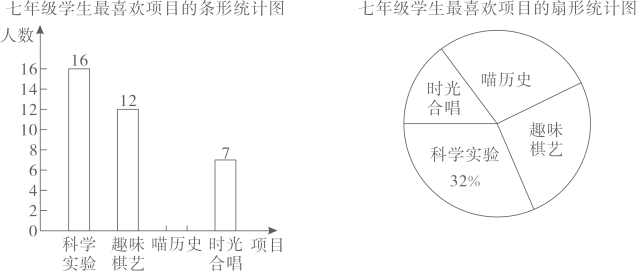(1)、本次被抽查的学生有多少名？

(2)、请补全条形统计图；“喵历史”项目所对应的扇形圆心角度数为多少度？

(3)、若该校七年级学生有600人，根据抽查结果，试估计全校七年级喜欢“趣味棋艺”项目的学生有多少人？

查看解析
2、先化简，再求值： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后再从1，2，3中选一个合适的数作为x的值，求式子的值.

查看解析
3、解下列方程（组）：

(1)、 ${\begin{array}{l} 2 x - y = 3 \\ x + y = 6 \end{array}$

(2)、 $\frac{2}{1 - x} + 1 = \frac{x}{1 + x}$

查看解析
4、计算：

(1)、 $(- 3)^{2} + (π + \sqrt{5})^{0} + 2^{- 2}$

(2)、 $(x + 1)^{2} + (x + 1) (x - 1)$

查看解析
5、现有甲、乙、丙三张不同的正方形纸片（如图1）.将三张纸片按图2，图3两种不同方式放置于同一矩形中，记图2中阴影部分周长为 $C_{1}$ ，面积 $S_{1}$ ；图3中阴影部分周长为 $C_{2}$ ，面积为 $S_{2}$ .已知 ${\begin{array}{l} 3 C_{1} = 2 C_{2} \\ S_{2} - S_{1} = \frac{1}{6} C_{1} C_{2} \end{array}$ ，则 $\frac{b}{a} - \frac{c}{b} =$ .

查看解析
6、甲、乙两个小马虎，在解方程组 ${\begin{array}{l} a x + y = 10 \\ x + b y = 7 \end{array}$ 时，由于粗心，甲看错了方程组中的a，得到方程组的解为 ${\begin{array}{l} x = 1 \\ y = 6 \end{array}$ ，乙看错了方程组中的b，得到方程组的解为 ${\begin{array}{l} x = - 1 \\ y = 12 \end{array}$ ，则原方程组正确的解是.

查看解析
7、若关于x的分式方程 $\frac{m}{x^{2} - 9} + \frac{2}{x + 3} = \frac{1}{x - 3}$ 有增根 $x = 3$ ，则m的值是.

查看解析
8、如图，已知AB//DE，∠B=75°，∠D=140°，则∠C=.

查看解析
9、某中学随机抽取了10名学生，统计他们上一年参与志愿者活动的次数，数据如下（单位：次）：3，5，2，4，3，6，4，5，3，1，则志愿者活动次数是3的频率是.

查看解析
10、已知方程3x+2y=6，用关于x的代数式表示y，则y=.

查看解析
11、若（x-2025）²+（x-2026）²=5，则（x-2025）（x-2026）的值是（）

A、-2 B、-1 C、1 D、2

查看解析
12、已知（2x-8）（3x-4）-（3x-4）（x-13）可分解因式为（3x+a）（x+b），则a+2b的值是（）

A、1 B、6 C、7 D、8

查看解析
13、如图，将三角形ABC沿BC方向平移得到三角形DEF，若BF=7，EC=1，则平移的距离是（）

A、3 B、4 C、6 D、8

查看解析
14、如图，直线AB与CD相交于点O，OB平分∠DOE.若∠DOE=60°，则∠AOE的度数是（）

A、140° B、150° C、160° D、170°

查看解析
15、下列多项式中，能运用平方差公式分解因式的是（）

A、 $- 4 x^{2} + 9 y^{2}$ B、 $- 4 x^{2} - 9 y^{2}$ C、 $4 x^{2} + 9 y^{2}$ D、 $4 x^{2} + 4 x y + y^{2}$

查看解析
16、计算 $(- a^{2})^{3}$ 的结果是（）

A、 $- a^{5}$ B、 $- a^{6}$ C、 $a^{5}$ D、 $a^{4}$

查看解析
17、质检部门为了检测某品牌电器的质量，从同一批次共10000件产品中随机抽取100件进行检测，检测出次品5件，由此估计这一批次产品中的次品件数是（）

A、5 B、100 C、500 D、1000

查看解析
18、空气由多种气体混合而成，为了直观介绍空气中各成分的百分比，最适合使用的统计图是（）

A、条形统计图 B、折线统计图 C、扇形统计图 D、频数直方图

查看解析
19、要使分式 $\frac{x - 2}{3 + x}$ 的值为0，则x的取值应满足（）

A、x≠-3 B、x≠2 C、x=-3 D、x=2

查看解析
20、如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法。配方法是一种重要的解决问题的数学方法，能解决一些与非负数有关的问题。如：求代数式的最大值或最小值等。求代数式x²+2x+2的最小值，同学们经过探究、合作、交流，最后得到如下解法：
解：x²+2x+2=（x²+2x+1²-1²）+2=（x+1）²+1. 因为（x+1）²是非负数，所以当（x+1）²=0时，（x+1）²+1的值最小，最小值为1，所以x²+2x+2的最小值是1.

(1)、求代数式y²-5y-4的最小值.

(2)、求代数式 $k^{2} + \frac{1}{k^{2}} + 5$ 的最小值.

(3)、求代数式 $k^{2} + 2 k + \frac{4}{k^{2}} - \frac{4}{k} + 3$ 的最小值.

查看解析

上一页 708 709 710 711 712 下一页跳转