-
1、下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2、如图1,已知点为外一点,、为的切线,切点分别为点、点 , 连接 , 点在优弧上运动,连接与交于另一点 , 与弦于点 .
 (1)、判断,对的打“√”,错的打“×”
(1)、判断,对的打“√”,错的打“×”①( )
②( )
③( )
(2)、如图2,若点为优弧的中点,且 , 求的值.(3)、如图1,设 , , 求关于的函数解析式. -
3、定义:若一次函数的图象与二次函数的图象有两个交点,并且都在坐标轴上,则称二次函数为一次函数的轴点函数.
 (1)、现有以下三个函数:①;②;③ , 其中 为函数的轴点函数.(填序号)(2)、函数(为常数,)的图象与轴交于点 , 其轴点函数与轴的另一交点为点 . 若 , 求的值.(3)、如图,函数(为常数,)的图象与轴、轴分别交于 , 两点,在轴的正半轴上取一点 , 使得 . 以线段的长度为长、线段的长度为宽,在轴的上方作矩形 . 若函数(为常数,)的轴点函数的顶点在矩形的边上,求的值.
(1)、现有以下三个函数:①;②;③ , 其中 为函数的轴点函数.(填序号)(2)、函数(为常数,)的图象与轴交于点 , 其轴点函数与轴的另一交点为点 . 若 , 求的值.(3)、如图,函数(为常数,)的图象与轴、轴分别交于 , 两点,在轴的正半轴上取一点 , 使得 . 以线段的长度为长、线段的长度为宽,在轴的上方作矩形 . 若函数(为常数,)的轴点函数的顶点在矩形的边上,求的值. -
4、如图,在四边形中, , 平分 , 交于点 , 作 , 交于点 , 与交于点 , 连接 , .
 (1)、求证:四边形是菱形;(2)、若 , , 求的长和的面积.
(1)、求证:四边形是菱形;(2)、若 , , 求的长和的面积. -
5、靖州杨梅享有“江南第一梅”的美誉,靖州作为杨梅之乡,当地政府为了把杨梅文化,打造成当地旅游名片,当地政府多次举办杨梅节活动.原来每盒杨梅进货价为100元,经过两次降价后每盒进货价为36元,并且每次降价的百分率相同.(1)、请问每次降价的百分率为多少?(2)、朴实水果店以36元每盒进货了200盒杨梅,计划以每盒标价50元出售.由于恰逢端午佳节,店铺准备开展大促销活动,所有商品一律八折.若要使200盒杨梅全部售出后的利润不少于2000元,则至少需要在促销活动开始前卖出多少盒?
-
6、如图,在中,点D在边上,且 . 在边上截取 , 过点E作交于点F.
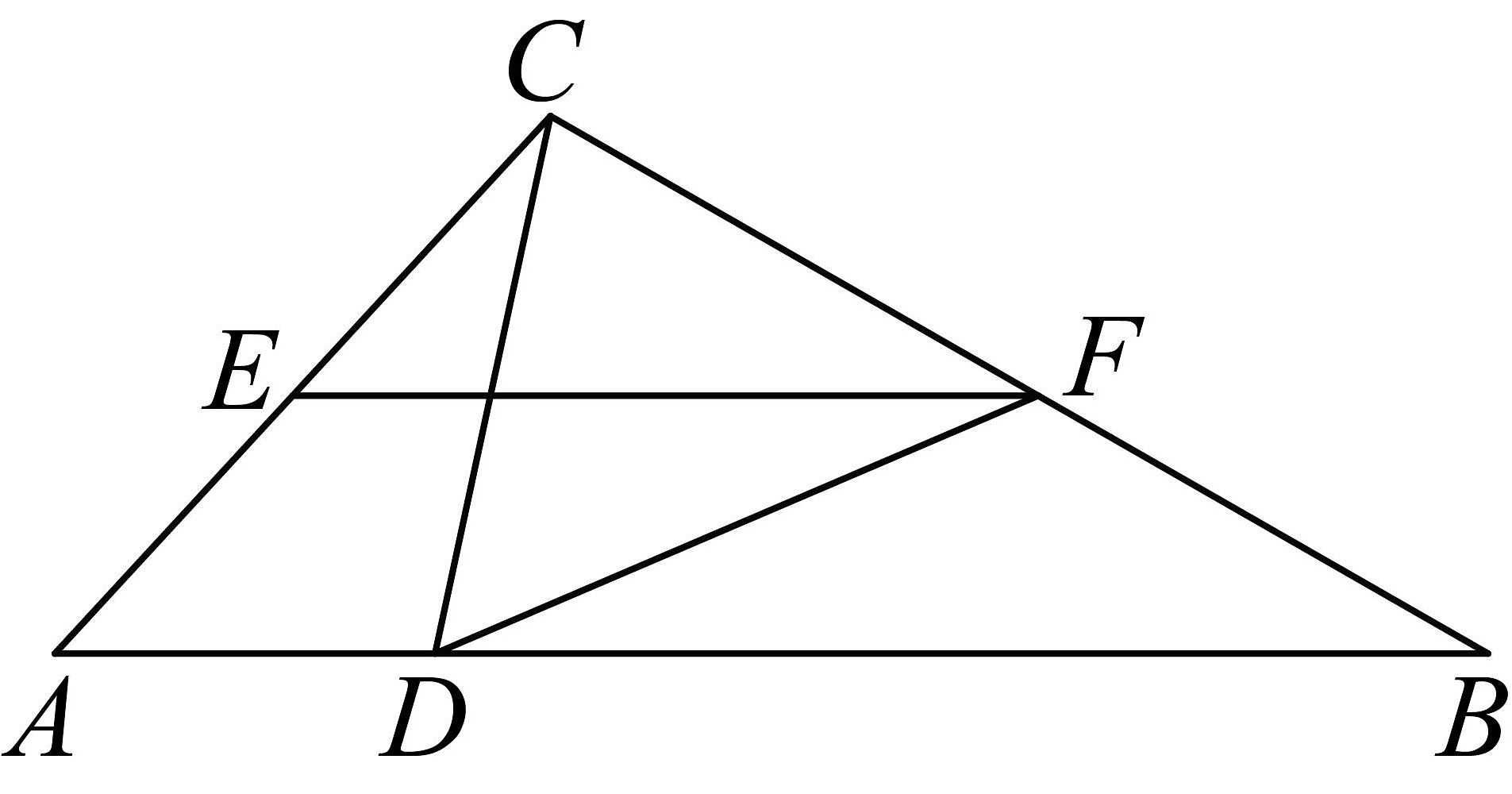 (1)、求证:;(2)、连接 , 若 , , 求的度数.
(1)、求证:;(2)、连接 , 若 , , 求的度数. -
7、教育部《关于加强中小学生安全教育工作的指导意见》,提高全校师生的安全防范意识和应急处理能力,开展了为期一个月的“安全教育月”主题活动.在此背景下,学校随机抽取部分同学进行了一次安全知识测试,按照测试成绩分为优秀、良好、合格和不合格四个等级,绘制了如下不完整的统计图.
安全知识测试成绩条形统计图 安全知识测试成绩扇形统计图
 (1)、参加测试的学生人数为______人,并将条形统计图补充完整.(2)、该校有名学生,请估计全校安全意识较强(测试成绩能达到良好以上等级)的学生有多少人?(3)、成绩为优秀的甲、乙两位同学被选中与其他学生一起参加安全宣讲活动,该活动随机分为 , , 三组,求甲、乙两人恰好分在同一组的概率.
(1)、参加测试的学生人数为______人,并将条形统计图补充完整.(2)、该校有名学生,请估计全校安全意识较强(测试成绩能达到良好以上等级)的学生有多少人?(3)、成绩为优秀的甲、乙两位同学被选中与其他学生一起参加安全宣讲活动,该活动随机分为 , , 三组,求甲、乙两人恰好分在同一组的概率. -
8、如图,在中, . 以点为圆心,以任意长为半径作弧交 , 于点 , , 以点 , 为圆心,以大于的长为半径分别作弧,两弧交于点 . 连接并延长交于点 .
 (1)、通过观察尺规作图的痕迹,可以发现射线是的______;(2)、若 , , 求的长.
(1)、通过观察尺规作图的痕迹,可以发现射线是的______;(2)、若 , , 求的长. -
9、先化简,再求值: , 其中
-
10、计算: .
-
11、已知甲、乙两名运动员10次标枪的平均成绩相同,标枪落点如图所示,则方差(填“”“”或“”).

-
12、 如图,已知抛物线交x轴于点A、点B,交y轴于点C,且点A(6,0),点C(0,4),AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
 (1)、求抛物线解析式及顶点坐标;(2)、求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;(3)、当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?(4)、是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
(1)、求抛物线解析式及顶点坐标;(2)、求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;(3)、当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?(4)、是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由. -
13、如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒2cm测得速度向点D移动,当点P到达点B处时,两点均停止移动,问:(1)、P,Q两点出发多长时间,线段PQ的长度为10cm?(2)、是否存在某一时刻,使四边形PBCQ为正方形?若存在,求出该时刻;若不存在,请说明理由.

-
14、平面直角坐标系内如图放矩形已知点 , . 将矩形沿折叠,使点与点重合.折痕交于点 , 交于点 .
 (1)、求点的坐标;(2)、若动点 , 同时从点出发,点以每秒个单位长度的速度向点运动,点以每秒个单位长度的速度沿射线方向运动,当点运动到点时停止运动,点也同时停止运动.设的面积为 , 点 , 的运动时间为秒,求与的函数关系式并直接写出自变量的取值范围;(3)、在(2)的条件下,是射线上的一点,点为平面内一点,是否存在点 , 使以 , , , 为顶点的四边形是正方形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求点的坐标;(2)、若动点 , 同时从点出发,点以每秒个单位长度的速度向点运动,点以每秒个单位长度的速度沿射线方向运动,当点运动到点时停止运动,点也同时停止运动.设的面积为 , 点 , 的运动时间为秒,求与的函数关系式并直接写出自变量的取值范围;(3)、在(2)的条件下,是射线上的一点,点为平面内一点,是否存在点 , 使以 , , , 为顶点的四边形是正方形?若存在,请求出点的坐标;若不存在,请说明理由. -
15、如图,抛物线与x轴交于 , D两点,与y轴交于点B,抛物线的对称轴与x轴交于点 , 点E,P为抛物线的对称轴上的动点.
 (1)、求该抛物线的解析式;(2)、当最小时,求此时点E的坐标;(3)、若点M为对称轴右侧抛物线上一点,且M在x轴上方,N为平面内一动点,是否存在点P,M,N,使得以A,P,M,N为顶点的四边形为正方形?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、当最小时,求此时点E的坐标;(3)、若点M为对称轴右侧抛物线上一点,且M在x轴上方,N为平面内一动点,是否存在点P,M,N,使得以A,P,M,N为顶点的四边形为正方形?若存在,求出点M的坐标;若不存在,请说明理由. -
16、如图,已知抛物线与轴交于点 , 与轴交于 , 两点.
 (1)、求抛物线的函数表达式;(2)、若点是第二象限抛物线上的动点,轴,交直线于点 , 点在轴上,点在坐标平面内,是否存在点 , 使以 , , , 为顶点的四边形是正方形?若存在,求点的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点是第二象限抛物线上的动点,轴,交直线于点 , 点在轴上,点在坐标平面内,是否存在点 , 使以 , , , 为顶点的四边形是正方形?若存在,求点的坐标;若不存在,请说明理由. -
17、如图,在平面直角坐标系中,二次函数的图象与轴交于 , 两点,顶点坐标为 .
 (1)、求二次函数的解析式;(2)、直线与相交于点 , 当为抛物线上第四象限内一点且时,求点D的坐标;(3)、为平面内一点,试判断坐标轴上是否存在一点 , 使以 , , , 为顶点的四边形为正方形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、直线与相交于点 , 当为抛物线上第四象限内一点且时,求点D的坐标;(3)、为平面内一点,试判断坐标轴上是否存在一点 , 使以 , , , 为顶点的四边形为正方形?若存在,请直接写出点的坐标;若不存在,请说明理由. -
18、综合与探究
如图,抛物线经过点和点 , 点是线段上一动点(不与重合),直线是抛物线的对称轴,设点的横坐标为 .
 (1)、求抛物线的函数表达式及直线的函数表达式.(2)、当点在直线右侧的线段部分上运动时,过点作轴的垂线交抛物线于点 , 分别过点作直线的垂线,垂足分别为 , 求四边形周长的最大值.(3)、若点是抛物线上一点,平面内是否存在点 , 使得以点为顶点的四边形是正方形时,若存在,请直接写出所有满足条件的点的坐标.若不存在,请说明理由.
(1)、求抛物线的函数表达式及直线的函数表达式.(2)、当点在直线右侧的线段部分上运动时,过点作轴的垂线交抛物线于点 , 分别过点作直线的垂线,垂足分别为 , 求四边形周长的最大值.(3)、若点是抛物线上一点,平面内是否存在点 , 使得以点为顶点的四边形是正方形时,若存在,请直接写出所有满足条件的点的坐标.若不存在,请说明理由. -
19、如图,已知直线与x轴交于点A,与y轴交于点B,线段的长是方程的一个根, . 请解答下列问题:
 (1)、求点A,B的坐标;(2)、直线交x轴负半轴于点E,交y轴正半轴于点F,交直线于点C.若C是的中点, , 反比例函数图象的一支经过点C,求k的值;(3)、在(2)的条件下,过点C作 , 垂足为D,点M在直线上,点N在直线上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
(1)、求点A,B的坐标;(2)、直线交x轴负半轴于点E,交y轴正半轴于点F,交直线于点C.若C是的中点, , 反比例函数图象的一支经过点C,求k的值;(3)、在(2)的条件下,过点C作 , 垂足为D,点M在直线上,点N在直线上.坐标平面内是否存在点P,使以D,M,N,P为顶点的四边形是正方形?若存在,请写出点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由. -
20、如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.
 (1)、求抛物线的解析式.(2)、Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)、若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.
(1)、求抛物线的解析式.(2)、Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)、若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.