-
1、为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,与地面平行,坐垫可沿射线方向调节.已知 , 车轮半径为 , 当时,小明体验后觉得骑着比较舒适,此时坐垫离地面高度约为?(结果精确到 , 参考数据: , , )
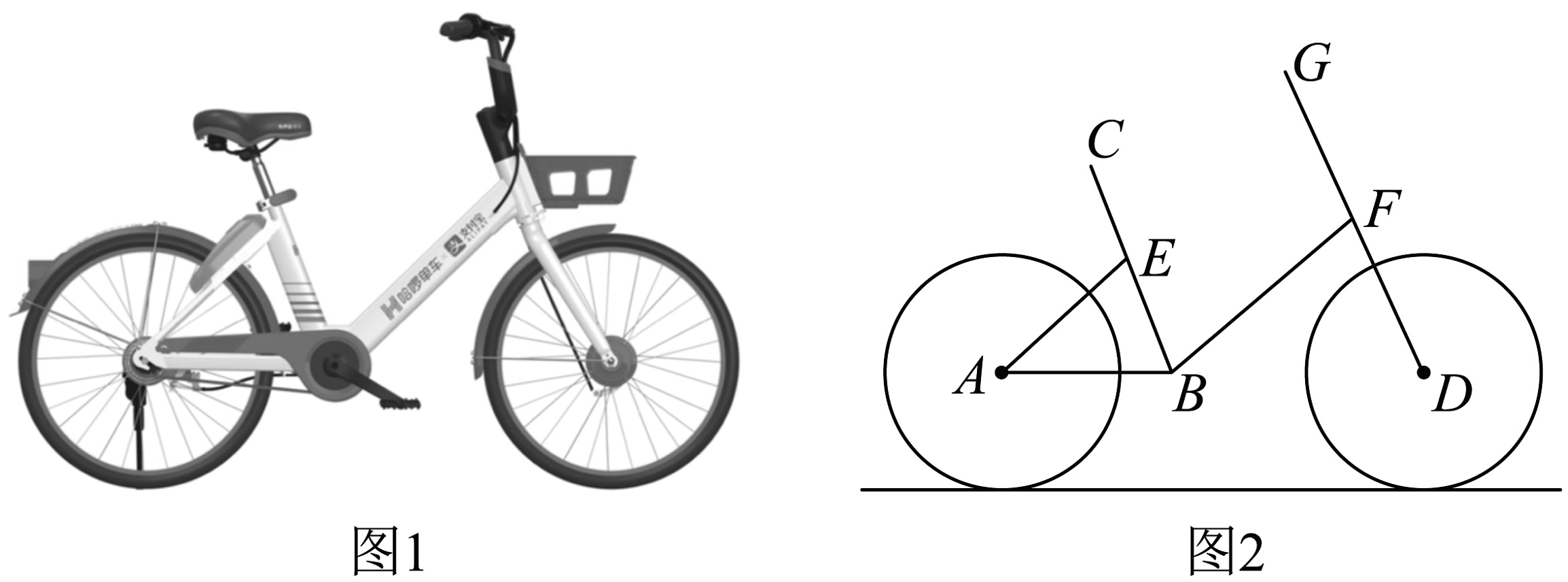
-
2、如图,矩形的顶点在的图象的一个分支上,点和点在边上, , 连接 , 轴,则的值为 .

-
3、如图,是一个模具的截面图,中间凹槽部分是一段圆弧,已知凹槽部分的宽 , 凹槽部分最深处 , 则凹槽所在圆的半径为..

-
4、如图所示,在矩形网格中,每个小正方形的边长为1,的三个顶点都在格点上,则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图,直线 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、截至年月日,《哪吒之魔童闹海》全球总票房(含预售及海外)已突破亿元人民币.该票房数值用科学记数法可表示为( )A、 B、 C、 D、
-
7、2025的绝对值是( )A、 B、 C、2025 D、
-
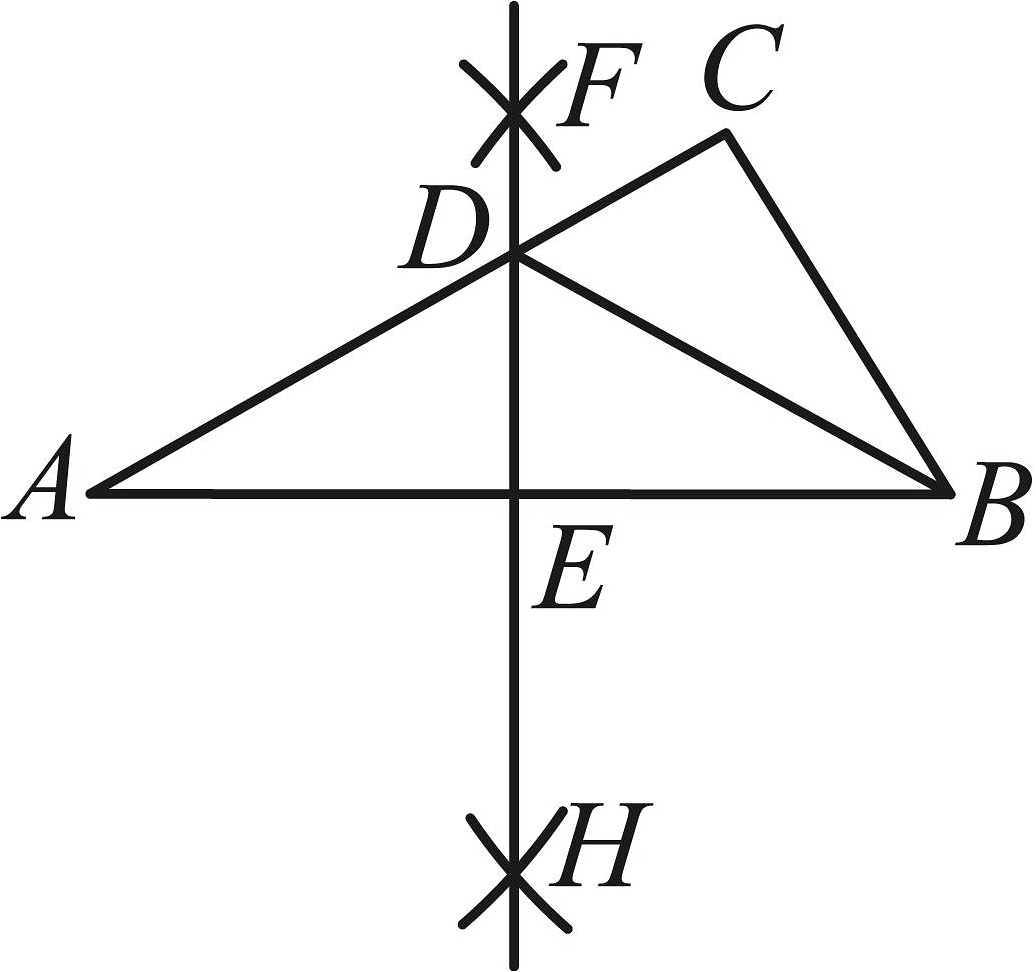
8、如图1,已知是的直径,为弦,点在上,连接交于点 , .
 (1)、求证:;(2)、如图2,为的切线,连接交于点 , 若为的平分线.求证:;(3)、如图3,在(2)的条件下,连接 , 若 , , 求的面积(结果用含的式子表示).
(1)、求证:;(2)、如图2,为的切线,连接交于点 , 若为的平分线.求证:;(3)、如图3,在(2)的条件下,连接 , 若 , , 求的面积(结果用含的式子表示). -
9、如图1,在平面直角坐标系中,已知二次函数的图象与轴交于点和点 , 与轴交于点 .
 (1)、求此抛物线的表达式.(2)、如图2,在抛物线的对称轴上是否存在点 , 使得四边形的周长最小?若存在,求出四边形周长的最小值及点的坐标;若不存在,请说明理由.(3)、将抛物线在轴以下的部分沿轴翻折,其余部分不变,得到新图象,如图3,若直线与此新图象有且仅有三个交点.求当时,代数式的最大值.
(1)、求此抛物线的表达式.(2)、如图2,在抛物线的对称轴上是否存在点 , 使得四边形的周长最小?若存在,求出四边形周长的最小值及点的坐标;若不存在,请说明理由.(3)、将抛物线在轴以下的部分沿轴翻折,其余部分不变,得到新图象,如图3,若直线与此新图象有且仅有三个交点.求当时,代数式的最大值. -
10、某校“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表(不完整).
课题
测量学校旗杆的高度
成员
组长:XXX组员:XXX,XXX,XXX
工具
皮尺等
测量示意图

说明:线段表示学校旗杆,垂直地面于点 .
第一次操作:如图①,将系在旗杆顶端的绳子自然下垂到地面,绳子多出的一段在地面拉直后记作 , 用皮尺测出的长度;
第二次操作:如图②,将绳子拉直,绳子末端落在地面的点处,用皮尺测出的长度.
测量数据
测量项目
数值(单位:米)
图①中的长度
1
图②中的长度
5
. .....
. ..
 (1)、根据以上测量结果,请你帮助这个小组求出学校旗杆的高度.(2)、如图③,第三次操作:某同学从点前行至点处,再次将绳子拉直,此时测得绳子末端到地面的距离的长度为1米,求该同学前进的距离的长度.
(1)、根据以上测量结果,请你帮助这个小组求出学校旗杆的高度.(2)、如图③,第三次操作:某同学从点前行至点处,再次将绳子拉直,此时测得绳子末端到地面的距离的长度为1米,求该同学前进的距离的长度. -
11、年月日至日,第四届湖南省旅游发展大会将在岳阳市举行,此次大会的吉祥物为“岳小楼”和“江小豚”,它们既展现了岳阳的历史韵味,又寓意着岳阳旅游的繁荣与吉祥.某玩具店看准商机,购进了一批“岳小楼”和“江小豚”的玩偶.已知购买个“岳小楼”玩偶和个“江小豚”玩偶共需元,购进个“岳小楼”玩偶和个“江小豚”玩偶共需元.
 (1)、请问每个“岳小楼”和“江小豚”玩偶的进价分别是多少元?(2)、该玩具店计划购进两种玩偶共个,且每个“岳小楼”玩偶的售价为元,每个“江小豚”玩偶的售价为元.若将所有玩偶全部售出,且利润不得低于元,则至少需要购进多少个“岳小楼”玩偶?
(1)、请问每个“岳小楼”和“江小豚”玩偶的进价分别是多少元?(2)、该玩具店计划购进两种玩偶共个,且每个“岳小楼”玩偶的售价为元,每个“江小豚”玩偶的售价为元.若将所有玩偶全部售出,且利润不得低于元,则至少需要购进多少个“岳小楼”玩偶? -
12、如图,在平行四边形中,是对角线上的两点(点在点左侧),且 .
 (1)、求证:四边形是平行四边形;(2)、若 , , , 求线段长.
(1)、求证:四边形是平行四边形;(2)、若 , , , 求线段长. -
13、为了引导师生走出教室、走向户外、走进阳光,享受更加健康活力的校园生活,促进学生身心健康发展.某学校严格落实教育部提出的要求,将课间时间延长至15分钟,分年级开展“阳光大课间”活动.九年级同学每天利用大课间时间进行跳绳训练,为了检验训练效果,九年级全体同学举办了一分钟跳绳比赛,并随机抽取了一部分同学一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如下统计图和表格:

等级
次数
频数
不合格
合格
良好
优秀
请结合上述信息完成下列问题:
(1)、此次抽取的学生人数为_____人;(2)、____,____;(3)、在扇形统计图中,“合格”等级对应的圆心角的度数是______;(4)、若该校九年级共有1200名学生,根据抽样调查结果,请估计该校九年级学生一分钟跳绳次数达到合格及以上的人数. -
14、计算:
-
15、如图1,先把一张矩形纸片对折两次,展开后得到三条折痕,设其中一条折痕为;如图2,再把点叠在折痕线上,得到 , 则:①;② .

-
16、已知 , 则代数式的值是 .
-
17、如图,中,分别以点、点为圆心、大于长为半径作弧,两弧相交于点 , , 作直线分别交 , 于点 , , 连接 , 若 , 的周长为 , 则的周长为 .
-
18、如图,直线 , 的直角顶点在直线上,点在直线上,若 , 则 .

-
19、人工智能分析平台最新发布的报告称,成为全球增长最快的工具,年月,其访问量达亿次.数据用科学记数法表示为 .
-
20、草莓中含有多种维生素,对人体健康有益.为了解甲、乙两个品种草莓的维生素含量,研究人员从甲、乙两个品种的草莓中各选5株,测量它们每百克草莓中维生素的含量(单位:毫克),在同等实验环境下,测得的数据统计结果如下:
品种
第一株
第二株
第三株
第四株
第五株
平均数
方差
甲
79
81
80
78
82
80
2
乙
80
77
79
83
81
80
4
则每百克草莓中维生素含量更稳定的是(填“甲”或“乙”).