相关试卷

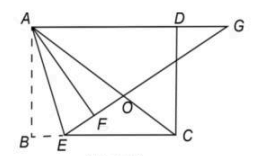
1、如图，矩形ABCD中，E是边BC上一点，将△ABE沿AE翻折，得到△AFE，延长EF交线段AD的延长线于点G，交线段AC于点0，若AB=2，BC=3，OC=0E，则线段DG的长为.

查看解析
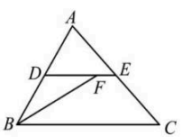
2、如图，点D、E分别为AB，AC的中点，BF平分∠ABC交DE于点F，若AB=4，BC=6，则EF=.

查看解析
3、如果a²-a-1=0，那么代数式（a-1）²+（a+2）（a-2）的值为

查看解析
4、如图，在平行四边形ABCD中，连接BD，且 $B D = C D$ ，过点A作 $A M ⊥ B D$ 于点M，过点D作 $D N ⊥ A B$ 于点N，且 $D N = 2 \sqrt{3}$ ，在DB的延长线上取一点P，满足 $∠ A B D = ∠ M A P + ∠ P A B$ ，则AP的长是（）

A、 $2 \sqrt{6}$ B、 $4 \sqrt{3}$ C、6 D、 $3 \sqrt{3}$

查看解析
5、对于抛物线 $y = - 2 (x - 1)^{2} + 3$ ，下列判断正确的是（）

A、抛物线的开口向上 B、抛物线的顶点坐标是 $(- 1, 3)$ C、当 $x = 3$ 时 $y > 0$ D、对称轴为直线 $x = 1$

查看解析
6、若关于x的一元二次方程 $(k - 1) x^{2} - 2 k x + k - 3 = 0$ 有实数根，则k的取值范围为（）

A、 $k \geq \frac{3}{4}$ B、 $k \geq \frac{3}{4}$ 且 $k \neq 1$ C、k≥0 D、 $k \geq 0$ 且 $k \neq 1$

查看解析
7、下列计算正确的是（）

A、a²+2a²=2a⁴ B、x·x²=x³ C、x+x²=x³ D、a³÷a=а

查看解析
8、中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，将这个数用科学记数法表示为（）

A、44x10⁸ B、4.4x10⁸ C、4.4×10⁹ D、4.4x10¹⁰

查看解析
9、下列各数中，比-2小的数是（）

A、0 B、-1 C、-3 D、1

查看解析
10、如图1，在平面直角坐标系xOy中，抛物线 $y = a (x + 2) (x - 3)$ 与x轴交于A，B两点，与y轴交于点C.连接BC， $O C = 2 O B$ .

(1)、求抛物线的表达式；

(2)、设点D在直线BC下方的抛物线上：
①如图2，连接OD，BD，CD，设 $△ O B D$ 的面积为 $S_{1}$ ， $△ B C D$ 的面积为 $S_{2}$ ，当 $S_{1} + S_{2}$ 的值最大时，求点D的坐标；
②如图3，连接AD，AC，交BC于点E，若 $△ E B A ~ △ A B C$ ，求点E的坐标.

查看解析
11、如图，四边形ABCD中.AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，

(1)、求证： $A C^{2} = A B \cdot A D$ ；

(2)、若 $A D = 4$ ， $A B = 6$ ，求 $\frac{A C}{A F}$ 的值.

查看解析
12、糖炒板栗是冬季深受大家喜爱的小吃.已知糖炒板栗每斤成本大约为10元.某夜市摊主试销阶段每斤的销售价×（元）与糖炒板栗日销售量义（斤）之间的关系如下表：
若日销售量y是销售价x的一次函数，试求：
x（元）
15
20
30
…
y（斤）
100
80
40
…

(1)、日销售量y（斤）与销售价x（元）的函数关系式：

(2)、假设后续销售情况与试销阶段效果相同，要使这种糖炒板栗每日销售的利润w最太，每斤的销售价应定为多少元？每日销售的最大利润是多少元？

查看解析
13、已知二次函数y=x²-4x+6

(1)、写出抛物线的开口方向、对称轴和顶点坐标.

(2)、当-1<x<3时，直接写出函数y的取值范围.

查看解析
14、一个布袋里装有三个小球，上面分别写着“塔”."山”.“石”·除文字外三个小球无其他差别.

(1)、从布袋里任意摸出一个小球，摸到文字恰好是“石"的概率

(2)、从布袋里任意摸出一个小球，记录其文字，放回并摇匀，再从中任意摸出一个小球记录其文字，求两次记录的文字有“塔"、"山"的概率.（要求列表或画树状图说明）

查看解析
15、已知 $\frac{a}{2} = \frac{b}{3}$ ，且 $2 a - b = 10$ ，求 $a + 2 b$ 的值

查看解析
16、如图，在 $△ A B C$ 中， $4 A B = 5 A C$ ， AD为 $∠ A B C$ 的角平分线，点 $E$ 在BC的延长线上， $E F ⊥ A D$ 于点 $F$ ，点 $G$ 在AF上， $F G = F D$ ，连结EG交AC于点 $H$ ，若点 $H$ 是AC的中点，则 $\frac{A G}{F D}$ 的值为.

查看解析
17、如图是一把折叠椅子及其侧面的示意图，把一个简易刻度尺与地面AB垂直放置，其中AB与“0"刻度线重合，O点落在“3"刻度线上，CD与"5"刻度线重合，若测得AB=50cm，则CD的长是.

查看解析
18、已知抛物线的顶点为（-2，3），且经过原点，则抛物线的解析式为.

查看解析
19、点P为线段AB的黄金分割点（AP>BP），若AB=2，则AP=.

查看解析
20、下表记录了某种幼树在一定条件下移植成活情况
移植总数п
400
1500
3500
7000
9000
14000
成活数m
325
1336
3203
6335
8073
12628
成活的频率（精确到0.01）
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是（精确到0.1）.

查看解析

上一页 146 147 148 149 150 下一页跳转

移植总数п	400	1500	3500	7000	9000	14000
成活数m	325	1336	3203	6335	8073	12628
成活的频率（精确到0.01）	0.813	0.891	0.915	0.905	0.897	0.902

x（元）	15	20	30	…
y（斤）	100	80	40	…