-
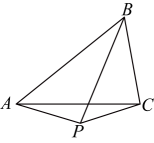
1、 如图,已知的面积为 , 为的角平分线,垂直于点 , 则的面积为 .
-
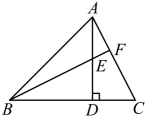
2、 如图,中,于D , E是上一点,连接并延长交于F , 若 , , , . 则的面积是 .
-
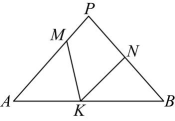
3、 如图,在中, , M、N、K分别是 , , 上的点,且 , . 若 , 则的度数为 .
-
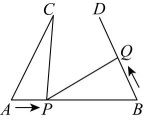
4、 如图, , , , 点P在线段上以的速度由点A向点B运动,点Q在线段上由点B向点D运动,两个动点同时出发,设运动时间为 , 则当点Q的运动速度为时,与有可能全等.
-
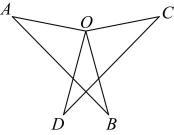
5、 如图, , , 则 .
-
6、 在中, , 是上一动点,连接 , 是三边垂直平分线的交点.连接 , , 若 , 则的最小值为( )A、 B、 C、3 D、
-
7、 如图,在中, , 为内一点,过点的直线分别交、于点、 . 若在的垂直平分线上,在的垂直平分线上,则的度数为 ( )
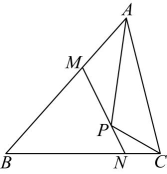 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 如图,在等腰三角形中, , 点为的中点,连结 . 以为边向左作 , 且 , . 连结 , 记和的面积分别为和 , 则的最大值是( )
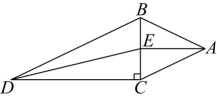 A、8 B、 C、 D、6
A、8 B、 C、 D、6 -
9、 将n个边长都为的正方形按如图所示的方法摆放,点 , , …,分别是正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积和为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、 如图,在中, , 平分 , , , 垂足分别为E , F , 已知 , . 求阴影部分面积为( )
 A、12 B、24 C、18 D、20
A、12 B、24 C、18 D、20 -
11、 如图,的三个顶点分别在小正方形的顶点(格点)上,称这样的三角形为格点三角形.那么图中与有一条公共边且全等(不含)的所有格点三角形的个数是( )
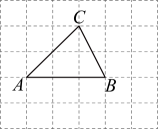 A、5个 B、6个 C、7个 D、8个
A、5个 B、6个 C、7个 D、8个 -
12、 如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
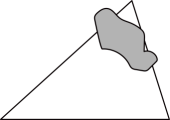 A、 B、 C、 D、
A、 B、 C、 D、 -
13、 如图,在中, , M是的中点,E是延长线上的动点,作交的延长线于点F . 记 , 当x , y的值发生变化时,下列代数式的值不变的是( )
 A、 B、 C、xy D、
A、 B、 C、xy D、 -
14、 如图,一束光线照射到平面镜上,然后在平面镜和之间来回反射,光线的反射角等于入射角.若 , 则的度数为( )
 A、50° B、55° C、63° D、65°
A、50° B、55° C、63° D、65° -
15、如图,P 是等边三角形ABC 中AC边上的动点(0°<∠ABP<30°),作△BCP 的外接圆交AB 于点 D. E 是圆上一点,且 , 连结 DE,BE,CE,DE 交BP 于点 F.
 (1)、 求证:BE=BC.(2)、当点 P 运动时,∠BFD 的度数是否发生变化?若发生变化,请说明理由;若不发生变化,求∠BFD 的度数.(3)、 探究线段BF,CE,EF 之间的数量关系,并证明.
(1)、 求证:BE=BC.(2)、当点 P 运动时,∠BFD 的度数是否发生变化?若发生变化,请说明理由;若不发生变化,求∠BFD 的度数.(3)、 探究线段BF,CE,EF 之间的数量关系,并证明. -
16、在一个圆中,有公共端点的直径与弦构成的图形内,平行于这条弦的半径称为这条弦的“F”形半径.
 (1)、 如图①,AB 为⊙O的直径,OP 是弦AC的“F”形半径.求证:(2)、 如图②,在△ABD 中,AB=AD,以AB为直径作⊙O,交AD 于点C,交BD 于点 P.求证:OP 是弦AC 的“F”形半径.(3)、 如图③,AB 为⊙O 的直径,OP 是弦AC的“F”形半径,在OP 的延长线上取一点 D,使 AD交. 于点E,连结CD,BD.若AB=10,CD= 求 AE的长.
(1)、 如图①,AB 为⊙O的直径,OP 是弦AC的“F”形半径.求证:(2)、 如图②,在△ABD 中,AB=AD,以AB为直径作⊙O,交AD 于点C,交BD 于点 P.求证:OP 是弦AC 的“F”形半径.(3)、 如图③,AB 为⊙O 的直径,OP 是弦AC的“F”形半径,在OP 的延长线上取一点 D,使 AD交. 于点E,连结CD,BD.若AB=10,CD= 求 AE的长. -
17、 如图①,C,D 是半圆 ACB 上的两点,若直径AB 上存在一点 P,满足∠APC =∠BPD,则称∠CPD 答案是 的“幸运角”.
 (1)、 如图②,AB 是⊙O 的直径,弦 CE⊥AB,D是. 上一点,连结 ED 交AB 于点P,连结CP,∠CPD 是的“幸运角”吗?请说明理由.(2)、 在(1)的条件下,设的度数为n,请用含n 的代数式表示的“幸运角”的度数.(3)、 如图③,在(1)的条件下,连结CD,直径AB=10,CD的“幸运角”为90°.
(1)、 如图②,AB 是⊙O 的直径,弦 CE⊥AB,D是. 上一点,连结 ED 交AB 于点P,连结CP,∠CPD 是的“幸运角”吗?请说明理由.(2)、 在(1)的条件下,设的度数为n,请用含n 的代数式表示的“幸运角”的度数.(3)、 如图③,在(1)的条件下,连结CD,直径AB=10,CD的“幸运角”为90°.①求弦CD 的长.
②当 时,求CE 的长.
-
18、婆罗摩笈多是公元7世纪古印度伟大的数学家,他研究过对角线互相垂直的圆内接四边形,我们把这类四边形称为“婆氏四边形”.如图,在⊙O 中,四边形ABCD 是“婆氏四边形”,对角线AC,BD 相交于点 E,过点E 作EH⊥DC 于点 H,延长HE交AB 于点F,则 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、 如图,AB 是⊙O 的直径,CD,EF 是⊙O的弦,且 AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )
 A、 B、10π C、24+4π D、24+5π
A、 B、10π C、24+4π D、24+5π -
20、如图,将半径为3 的圆形纸片,按下列顺序折叠两次.若折叠后的 和 都经过圆心O,则图中阴影部分的面积是.
