-
1、二次函数在范围内有最小值 , 则的值为 .
-
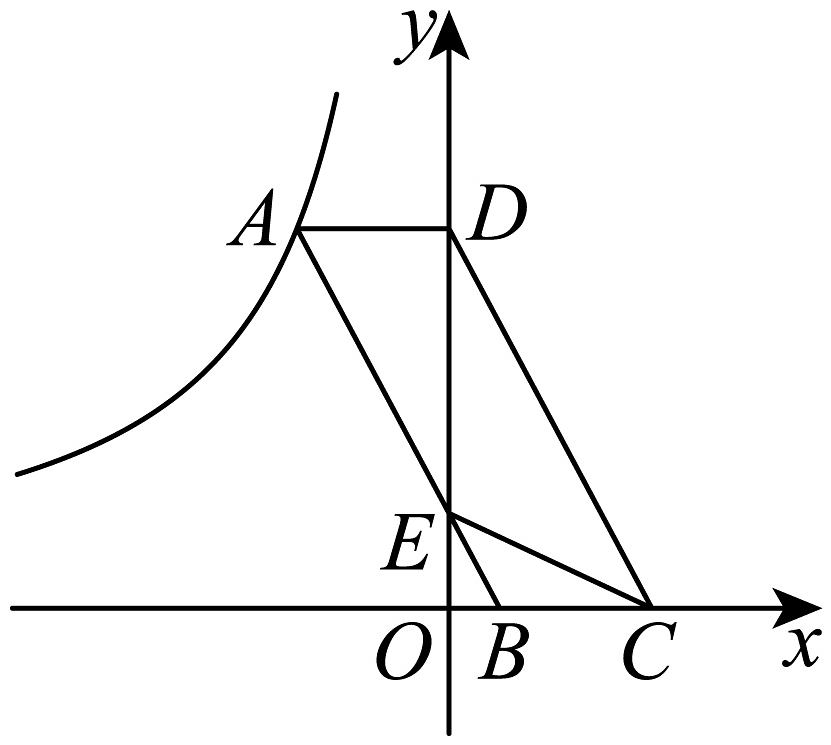
2、如图,的顶点在反比例函数的图象上,点在轴上,点 , 在轴上,与轴交于点 , 连接 , 若 , , 则的面积为 .
-
3、如图,是一条弦,将劣弧沿弦翻折,连接并延长交翻折后的弧于点 , 连接 , 若 , , 则的直径为 .

-
4、四边形和都是正方形,E在上,连接交对角线于点H,交于点I.若要求两正方形的面积之和,则只需知道( )
 A、的长 B、的长 C、的长 D、的长
A、的长 B、的长 C、的长 D、的长 -
5、如图所示,已知平行四边形和平行四边形相似,且平行四边形的面积是平行四边形的 , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知圆心角为的扇形的半径为6,则扇形的弧长为( )A、 B、 C、 D、
-
7、已知:如图,在中,于点D,为上一点,且 , 交于点 .
 (1)、求证:;(2)、连接 , 作交于点G,求证:;(3)、若 , 求的长.
(1)、求证:;(2)、连接 , 作交于点G,求证:;(3)、若 , 求的长. -
8、已知关于x、y的方程组的解都为非负数.(1)、求a的取值范围;(2)、已知 , 求的取值范围;(3)、已知(m是大于1的常数),且 . 求的最大值.(用含m的代数式表示)
-
9、如图,在中,是角平分线,是高.
 (1)、若 , , 垂足为F,求的度数;(2)、若 , (>),求的度数(用含有 , 的代数式表示).
(1)、若 , , 垂足为F,求的度数;(2)、若 , (>),求的度数(用含有 , 的代数式表示). -
10、已知关于的不等式 .(1)、若是该不等式的解,求的取值范围;(2)、在(1)的条件下,且不是该不等式的解,求的范围.
-
11、在爆破时,如果导火索燃烧的速度是 , 人跑开的速度是 , 那么要使点导火索的施工人员在点火后能够跑到以外(包括)的安全地区,这根导火索的长度至少应取多少米?
-
12、如图,已知 , , .
 (1)、求证:;(2)、若 , , 求的度数.
(1)、求证:;(2)、若 , , 求的度数. -
13、解不等式(组),并把(2)的解集在数轴上表示出来.(1)、;(2)、 .
-
14、如图,设长方形的长 , 宽 , , 且 , 则 . (填“”或“”或“”)

-
15、如图,点、、在同一直线上,若 , , , 则 .

-
16、若 , 且 , , 设 , 则t的取值范围为( )A、 B、 C、 D、
-
17、如图,在中, , , , 为边的垂直平分线,点D为直线上一动点,则的周长的最小值为( )
 A、10 B、12 C、14 D、15
A、10 B、12 C、14 D、15 -
18、若 , 则下列不等式中一定成立的是( )A、 B、 C、 D、
-
19、如图,已知 , 补充下列条件中的一个后,仍不能判定的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、学校决定六年级两个班开展“古诗文诵读”活动,要求每个学生购买一本单价为5元的《古诗文读本》.学校与书店商议,书店对一次购买达到50本以上的给予的优惠,一次购买达到100本及以上给予的优惠,现有情况是:六(一)班有48人,六(二)班有49人,学校请你计算一下,怎么买最合理?说明理由.