-
1、在平面直角坐标系中,点A(3,1)关于x轴对称的点A'的坐标是.
-
2、 如图,∠ABC=120°,D 是∠ABC平分线上一点,过点 D 作DE∥BC,交AB 于点 E,作DF⊥BC 于点 F,DF=a,BD=b,则△BDE的面积为 ( )
 A、ab B、ab C、a+b D、2ab
A、ab B、ab C、a+b D、2ab -
3、七巧板是我国一种传统益智玩具,由宋代的“燕几图”演变而来.如图所示的七巧板由五块等腰直角三角形、一块正方形和一块平行四边形拼成,则下列说法:①△ABH≌△ADH;②△CFJ≌ △AHD;③ △BEF ≌ △GHI;④△GHI≌△FCJ,其中正确的有 ( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
4、 如图,△ABC为等边三角形,BD⊥BC,AD⊥BD,若AD=3,则△ABC的周长为 ( )
 A、9 B、12 C、15 D、18
A、9 B、12 C、15 D、18 -
5、下面是作业本上的一道习题,小可,小雨,小齐,小梦四位同学的作法中,错误的是( )
题目:
如图,在△ABC 中,∠B=80°,∠C=40°,借助尺规,在直线AC 上找一点 D,连接 BD,使得∠CBD=∠C.
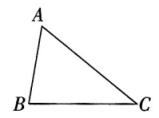 A、
A、 小可的作法
B、
小可的作法
B、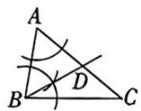 小雨的作法
C、
小雨的作法
C、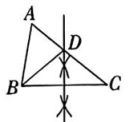 小齐的作法
D、
小齐的作法
D、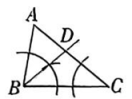 小梦的作法
小梦的作法
-
6、如图,在四边形ABCD 中,AC 垂直平分BD,若AD=3,BC=2,则四边形ABCD 的周长为 ( )
 A、7 B、8 C、9 D、10
A、7 B、8 C、9 D、10 -
7、 如图,△ABC≌△DEF,则x的值为 ( )
 A、25 B、27 C、38 D、65
A、25 B、27 C、38 D、65 -
8、如图①是一款户外投影幕布支架,其侧面示意图如图②所示,组装好之后,两边的拉绳长度相等,支杆 AD 与底座 BC 的衔接点D 正好是底座 BC 的中点,小可测得∠BAD=18°,则两根拉绳之间的夹角∠BAC 的度数为 ( )
 A、28° B、30° C、36° D、42°
A、28° B、30° C、36° D、42° -
9、下列长度的三条线段中,能构成三角形的是 ( )A、1,2,3 B、3,4,5 C、5,6,12 D、3,5,8
-
10、 民族服饰被史学家称之为“穿在身上的史书”.在下列展示的民族服饰图片中,轴对称图形有 ( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
11、下列图形具有稳定性的是 ( )A、
 B、
B、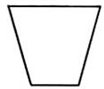 C、
C、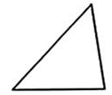 D、
D、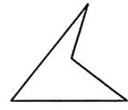
-
12、【操作过程】如图①是一个长为2a,宽为2b的长方形,按图中虚线将其分成四个相等的小长方形后,再将四个小长方形拼成如图②所示的正方形.

【探究发现】
(1)、请试着用两个不同的式子表示图②中阴影部分的面积:方法①: ,
方法②:;
(2)、由(1)可以得到的一个等式为;(3)、【类比应用】若 求 的值;(4)、【知识迁移】如图③,张伯伯打算在长方形菜地ABCD 旁边,分别以AB,AD为边向外用篱笆围出正方形ABEF 与正方形ADGH两块新菜地(不包含长方形ABCD 的边长).已知张伯伯一共用了210 m长的篱笆,两块新菜地的面积和为 , 求长方形菜地ABCD的面积. -
13、(1)、【初次探究】观察下列两组数据,你能发现什么规律?
①40×40,45×35,62×18,74×6
②50×50,52×48,73×27,92×8
(2)、【猜想证明】请你利用本节知识证明(1)中发现的规律;
(3)、【实践应用】如图,某中学准备在校园里建一个长方形花园,要求一面靠墙(墙的长度为35m),现用总长为60m的材料围成一个长方形花园如图所示,当AB为多少时,长方形花园的面积最大,最大面积是多少?

-
14、如果一个正整数能表示为两个连续正奇数的平方差,那么称这个正整数为“奇特数”,如 因此8,16,24这三个数都是奇特数.(1)、56,63是奇特数吗? 为什么?(2)、小明根据上述运算得到“两个连续正奇数的平方差能被8整除”的结论,请你判断他的结论是否正确,并说明理由.
-
15、小可作业本上的一道题目及解题过程如下,请完成以下问题:
先化简,再求值:
其中a=3,b=-1.
解:原式 第一步
第二步
=-8a-2b, 第三步
当a=3,b=-1时,原式=-24+2=-22. 第四步
(1)、小可的解题过程从第步开始出错,原因是;(2)、请你帮小可写出正确的解题过程. -
16、已知 求证:3a+c=3b.
-
17、先化简,再求值:(2a+3)(2a-3)+ 其中
-
18、计算:(1)、(2)、
-
19、观察下列图形:它们是按一定规律排列的,第1个图形中阴影部分的面积为3,第2个图形中阴影部分的面积为8,第3个图形中阴影部分的面积为15,…,依照此规律,第4个图形中阴影部分的面积为;第n个(n为正整数)图形中阴影部分的面积为(用含n的代数式表示).

-
20、学习完整式的乘法后,老师将3张分别写有数字的卡片分给3位学生,要求他们根据自己手中的卡片上的数值选择合适的位置(值越大,站的位置越高),则站在1号位置的同学是.
