-
1、如图所示，∠A=75°，∠B=65°，将纸片的一角折叠，使点C落在△ABC内部，若∠1=45°，则∠2=°.
-
2、如图所示，已知△ABC≌△DEF，点B，E，C，F依次在同一条直线上.若BC=8，CE=5，则CF的长为.
-
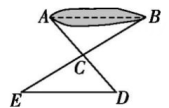
3、如图所示，有一池塘，要测池塘两端A，B的距离，可先在地上取一个点C，从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE.根据两个三角形全等，可知量出的DE的长就是A，B的距离.判定图中两个三角形全等的依据是.
-
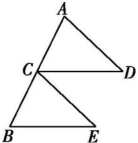
4、如图所示，C是AB的中点，且CD=BE，请添加一个条件 ， 使得△ACD≌△CBE.
-
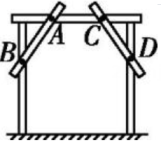
5、赵师傅做完门框后，为防止变形，按如图所示方式在门上钉上两根斜拉的木条(即图中的AB，CD两根木条)，这其中的数学原理是.
-
6、如图所示，小刚站在河边的点A处，在河的对面(小刚的正北方向)的B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了30步到达一棵树C处，接着再向前走了30步到达D处，然后他左转90°直行，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他一共走了140步.如果小刚一步大约50 cm，估计小刚在点A处时他与电线塔的距离为( )
A、40 m B、50 m C、60 m D、70 m -
7、如图所示，△ABC是格点三角形(顶点在网格线交点的三角形)，则在图中能够作出与△ABC全等，且与△ABC有一条公共边的格点三角形(不含△ABC)的个数是( )
A、1 B、2 C、3 D、4 -
8、如图所示，在△PAB中，∠A=∠B，M，N，K分别是PA，PB，AB上的点，且AM=BK，AK=BN，若∠MKN=42°，则∠P的度数为( )
A、44° B、66° C、96° D、92° -
9、如图所示，在△ABC和△DEF中，点A，E，B，D在同一条直线上，AC∥DF，AC=DF，只添加一个条件，不能判定△ABC≌△DEF的是( )
A、AE=DB B、∠C=∠F C、BC=EF D、∠ABC=∠DEF -
10、根据下列已知条件，能画出唯一的△ABC的是( )A、AB=5，BC=4，AC=1 B、AB=5，AC=4，∠B=60° C、∠A=30°，∠B=60°，∠C=90° D、∠A=30°，∠B=60°，AB=5
-
11、如图所示，若△ABC≌△ADE，则下列结论中一定成立的是( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED -
12、如图所示，在△ABC中，∠BAC=60°，∠B=50°，AD∥BC，则∠1的度数为( )
A、50° B、60° C、70° D、80° -
13、如图所示，在△ABC中，AD是高，AE是中线，AD=4，S△ABC=12，则BE的长为( )
A、1.5 B、3 C、4 D、6 -
14、用一根小木棒与两根长度分别为3 cm，5 cm的小木棒组成三角形，则这根小木棒的长度可以是( )A、9 cm B、7 cm C、2 cm D、1 cm
-
15、下列四组图形中，不是全等图形的是( )A、
B、
C、
D、
-
16、“一线三等角”模型是平面几何图形中的重要模型之一，“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况，在学习过程中，我们发现“一线三等角”模型的出现，还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题：
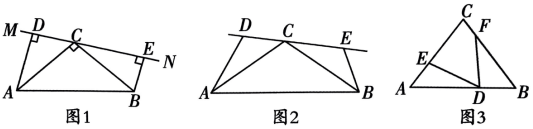(1)、如图 1， 猜想DE，AD，BE之间的关系；(2)、如图2，将(1)中条件改为. 请问(1)中的结论是否成立?若成立，请给出证明；若不成立，请说明理由；(3)、如图3，在中，点D为AB上一点， ， 请直接写出AB的长. -
17、将一副三角板拼成如图所示的图形，过点C作CF平分交 DE于点F.
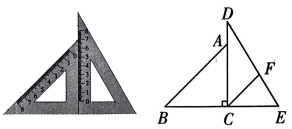(1)、求证： ∥(2)、求 的度数. -
18、在中，点D是BC的中点.
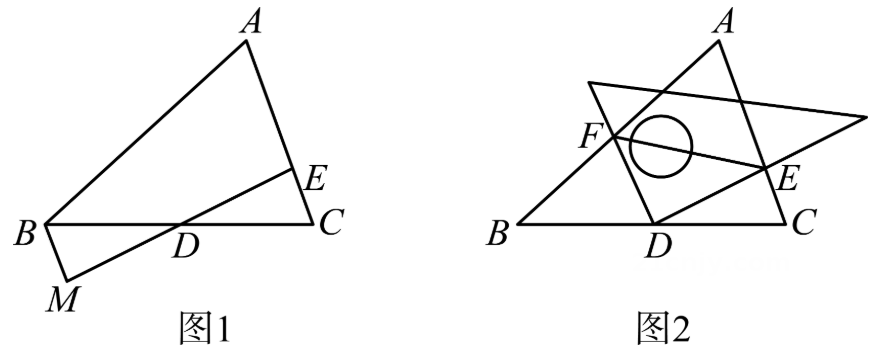(1)、如图 1，在边 AC 上取一点E，连接ED，过点B作∥AC交 ED 的延长线于点M，求证：(2)、如图2，将一直角三角板的直角顶点与点 D 重合，另两边分别与AC，AB 相交于点E，F，求证： -
19、如图，已知在△ABC 中， D 为边BC 延长线上一点，BM 平分 E 为射线 BM 上一点，连接CE.
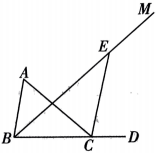(1)、若CE∥AB，求∠BEC的度数；(2)、若CE 平分∠ACD，求. 的度数. -
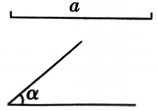
20、已知：线段 a，∠α，求作： 使 ∠B=∠α.
