-
1、若 , 且 , 则的值为 .
-
2、分解因式:(1)、;(2)、 .
-
3、若多项式可以因式分解成 , 则的值是 .
-
4、已知 , 且 , 则的值为( )A、 B、2024 C、 D、4048
-
5、若在整数范围内可以进行因式分解,则常数a的值有( )个A、2 B、4 C、6 D、8
-
6、给出下面四个多项式:①;②;③;④ , 其中含因式的多项式有( )A、1个 B、2个 C、3个 D、4个
-
7、计算的结果是( )A、 B、 C、0 D、
-
8、下列多项式中,可以用完全平方公式进行因式分解的是( )A、 B、 C、 D、
-
9、多项式中,能用完全平方公式分解因式的有( )A、0个 B、1个 C、2个 D、3个
-
10、长和宽分别为的长方形,它的周长为14,面积为10,则的值为( )A、2560 B、490 C、80 D、49
-
11、下列各式中,分解因式正确的是( )A、 B、 C、 D、
-
12、下列能用平方差公式进行因式分解的是( )A、 B、 C、 D、
-
13、如图,在一条不完整的数轴上从左到右有A,B,C三点,其中 A,B 两点的距离为3,B,C 两点的距离为1.设点 A,B,C 所对应的数的和是m,积是n.
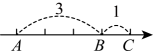 (1)、①若以点B为原点,写出点 A,C所对应的数,并计算m的值;
(1)、①若以点B为原点,写出点 A,C所对应的数,并计算m的值;②若以点C为原点,m又是多少?
(2)、若原点O在图中数轴上点C的右边,且点C与原点的距离为4,求n的值. -
14、如图,数轴上点表示的倒数,点表示的绝对值,点表示 .
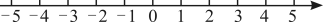 (1)、写出 , , 表示的数,并在数轴上描出 , , 三个点;(2)、若把数轴的原点取在点处,、、每两点之间的距离不变,求出此时点和表示的数.
(1)、写出 , , 表示的数,并在数轴上描出 , , 三个点;(2)、若把数轴的原点取在点处,、、每两点之间的距离不变,求出此时点和表示的数. -
15、计算(1)、;(2)、 .
-
16、用十进制计数法表示正整数,如 , 用二进制计数法来表示正整数,如: , 记作: , 记作: , 则表示数 .
-
17、定义一种新运算“”: , 比如: . 则 .
-
18、若 , , 且 , 且 , 那么的值是 .
-
19、我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,按照从右到左的顺序满五进一,即“结绳计数”.某天两同学背单词比赛,如图①是同学和同学在绳子上打结记录的背单词的总数量,图②是同学比同学多背诵的单词数量.则在这一天,同学背诵的单词数量是( )
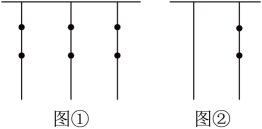 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个 -
20、如图数轴上两点表示的数分别为 , , 则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、