-
1、已知关于x的一元二次方程 .(1)、若方程有实数根,求实数m的取值范围.(2)、若等腰三角形的其中一边为3,另两边是这个方程的两根,求m的值.
-
2、在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度(米)与水平距离(米)之间的关系式为 , 小宇此次实心球训练的成绩为多少米.

-
3、如图,在平面直角坐标系中,点、、的坐标分别为 , , .
 (1)、画出将绕点逆时针方向旋转后得;(2)、求的长.
(1)、画出将绕点逆时针方向旋转后得;(2)、求的长. -
4、已知抛物线 .(1)、求其对称轴和顶点坐标;(2)、若 , 在此抛物线上,比较的大小.
-
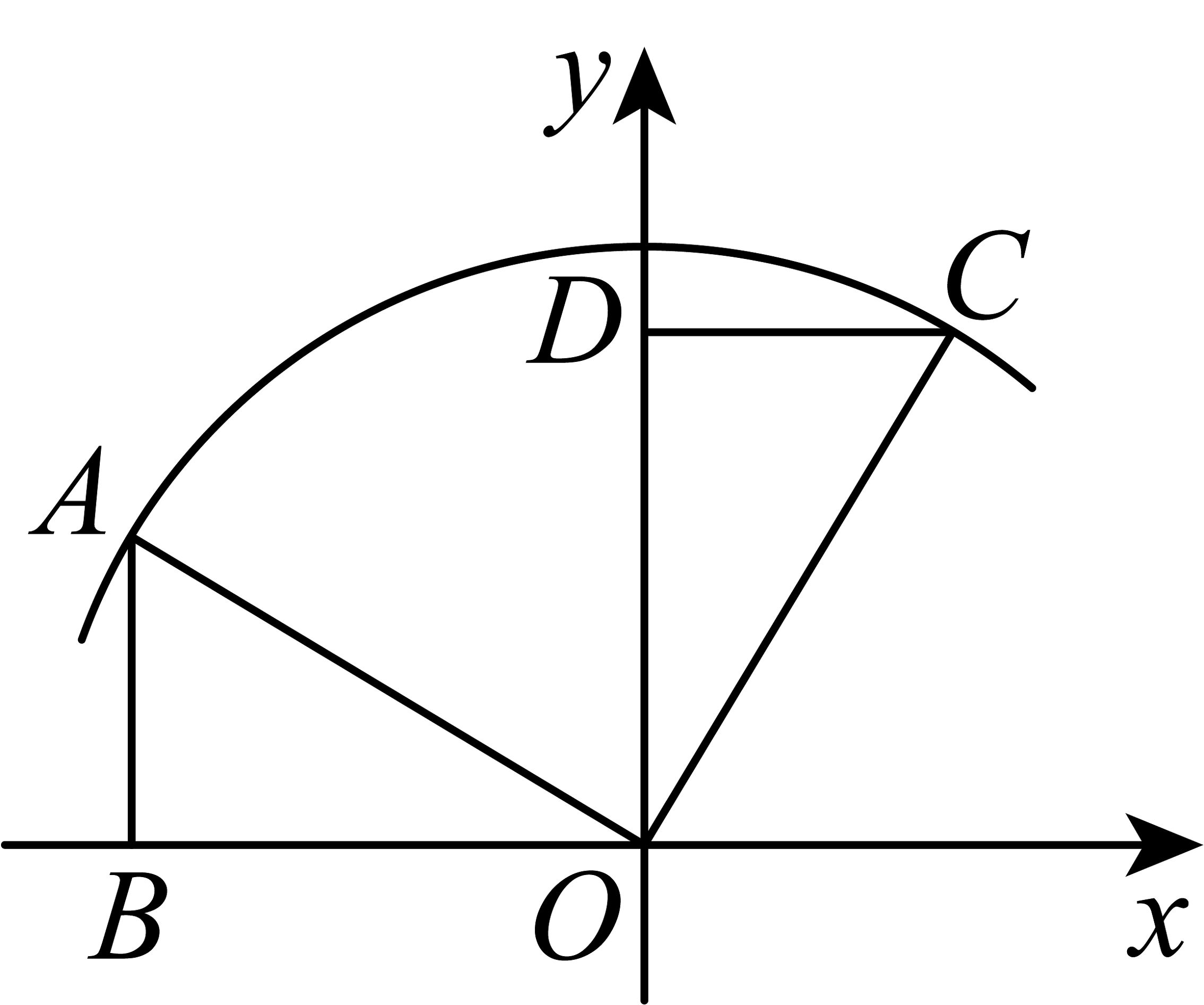
5、如图,在平面直角坐标系中,绕原点顺时针旋转 , 得到 , 若 , , 则旋转后点的坐标为 .
-
6、抛物线和轴有公共点,则的取值范围是 .
-
7、若是某个一元二次方程的根,则这个一元二次方程可以是( )A、 B、 C、 D、
-
8、第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行,中国取得金牌榜第一名的好成绩,如图所示巴黎奥运会项目图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
9、如图在平面直角坐标系中,已知点A(﹣6,0),点B(0,6)分别在坐标轴上,连接AB.
(1)求∠ABO的度数;
(2)动点P从原点O出发,沿x轴向右每秒1个单位长度的速度运动,运动时间为t秒,当△ABP为等腰三角形时,直接写出t的值(点P不与点O重合);
(3)动点P从原点O出发,沿x轴向左每秒1个单位长度的速度运动,运动时间为t秒,当∠PBO=∠PAB时,直接写出t的值.

-
10、已知一次函数 .(1)、若随增大而减小,求的取值范围;(2)、若其图象与直线的交点在轴上,求的值;(3)、若其图象不经过第二象限,且为整数,求的值.
-
11、在平面直角坐标系中,已知点 , 分别根据下列条件,求点的坐标.(1)、点到轴的距离为1,且在轴的右侧;(2)、点的坐标为 , 且轴.
-
12、计算: .
-
13、如图,在平面直角坐标系中,已知正方形 , , 点为轴上一动点,以为边在的右侧作等腰 , , 连接 , 则的最小值为 .

-
14、已知点在函数的图像上,则 .
-
15、若一个正数的两个平方根分别为和 , 则这个数是 .
-
16、甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离与甲车行驶的时间之间的函数关系如图,下列结论正确的有( )个

①A、B两城相距300千米;
②甲车比乙车早出发1小时,却晚到1小时;
③相遇时乙车行驶了2.5小时;
④当甲乙两车相距50千米时,t的值为或或或
A、1 B、2 C、3 D、4 -
17、已知是一次函数图象上两个不同的点,以下判断正确的是( )A、 B、 C、 D、
-
18、下列各式中,一定是二次根式的是( )A、 B、 C、3 D、
-
19、的相反数为( ).A、 B、2024 C、 D、
-
20、如图,已知二次函数的图象与x轴交于A,B两点.A点坐标为 , 与y轴交于点 , 点M为抛物线顶点,点E为AB中点.
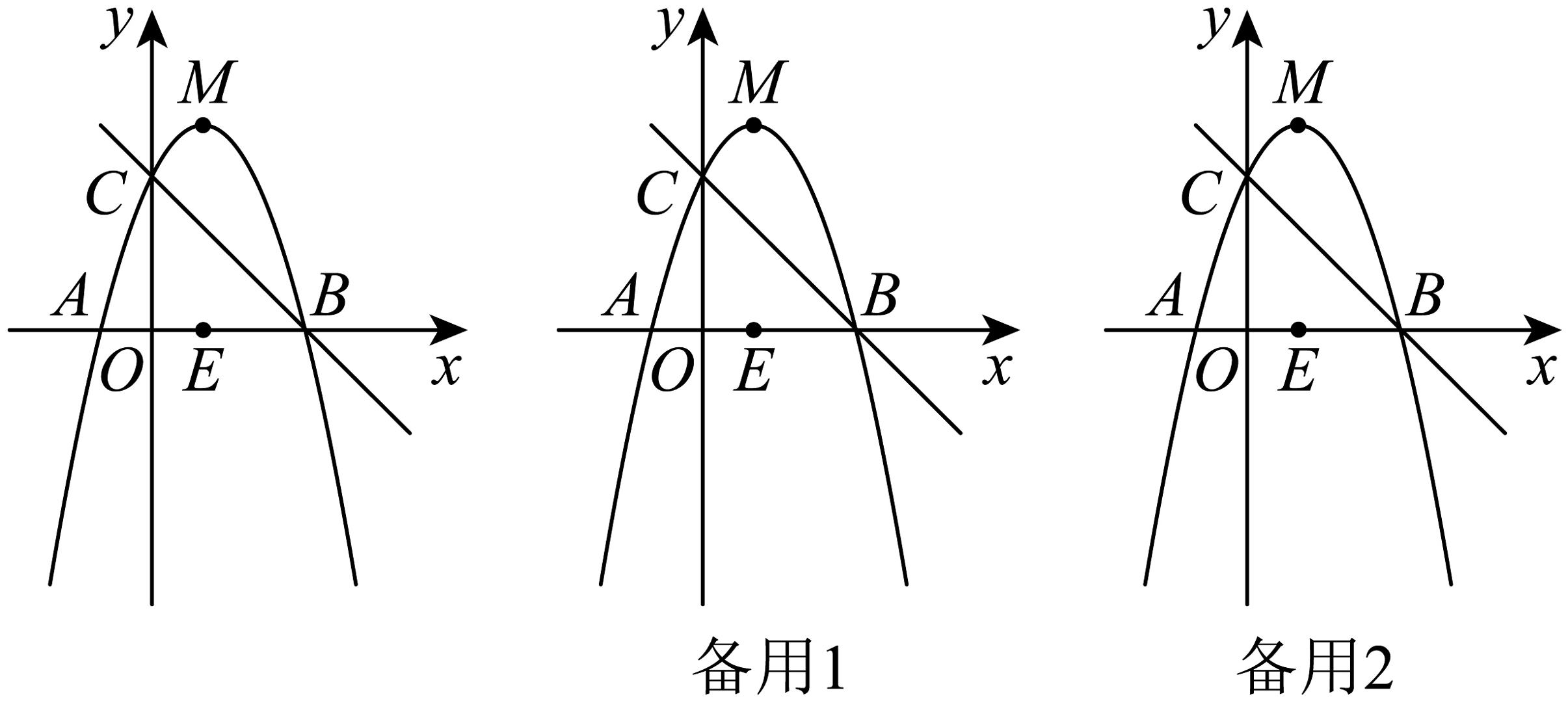 AI(1)、求二次函数的表达式;(2)、在直线BC上方的抛物线上存在点Q,使得 , 求点Q的坐标;(3)、已知D,F为抛物线上不与A,B重合的相异两点,若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,当D,E,F三点共线时,试判断的面积是否为定值,若是,请求出定值:若不是,请说明理由.
AI(1)、求二次函数的表达式;(2)、在直线BC上方的抛物线上存在点Q,使得 , 求点Q的坐标;(3)、已知D,F为抛物线上不与A,B重合的相异两点,若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,当D,E,F三点共线时,试判断的面积是否为定值,若是,请求出定值:若不是,请说明理由.