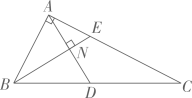
-
1、如图，在 Rt△ABC中，AD，BE 分别是△ABC的中线和角平分线，AD⊥BE于点N，AD=8，求 AC的长.
-
2、 如图，将一张三角形纸片 ABC的一角折叠，使点 A落在△ABC外的A'处，折痕为DE.如果 那么下列式子中正确的是（ ）
A、γ=2α+β B、γ=α+2β C、γ=α+β -
3、 将一副三角板按如图方式重叠，则∠1的度数为（ ）
A、45° B、60° C、75° D、105° -
4、如图，在△ABC中，AC<AB<BC.
(1)、如图①，已知线段 AB 的垂直平分线与BC 边交于点 P，连结 AP.求证：∠APC=2∠B.(2)、如图②，以点 B 为圆心，线段 AB 的长为半径画弧，与BC 边交于点Q，连结 AQ.若∠AQC=3∠B，求∠B的度数. -
5、 如图，点 B 在线段 AE上，点 D 在线段 AC 上，AB= AD. 要 证 △ABC≌△ADE：
(1)、添加的条件是 ， 所用的判定方法是ASA；(2)、添加的条件是 ， 所用的判定方法是AAS；(3)、添加的条件是 BE=CD，所用的判定方法是；(4)、能不能添加条件“BC=DE”? （填“能”或“不能”） -
6、 如图，已知△ABC≌△ADE.
(1)、若△ADE的周长为12，AB=3，BC=5，则 AC的长为；(2)、若∠B=70°，∠C=25°，∠DAC=25°，则∠EAC=. -
7、
性质
全等三角形的对应边 ， 对应角 ， 周长 ， 面积
判定
SSS， ， ， 直角三角形全等特有的判定方法：
-
8、如图，在△ABC中，AH 是高线，EF 是中位线.若∠CAH=30°，EF=2，则CH 的长度为（ ）
A、2 B、 C、3 D、2 -
9、 如图，在△ABC中，E是中线AD 的中点.若△AEC的面积是1，则△ABD的面积是.
-
10、 如图，在△ABC中，AD 平分∠BAC，DE⊥AB. 若 AC=2，DE=1，则S△ACD=.
-
11、
角平分线
AD是△ABC的角平分线⇔
中线
AE 是△ABC的中线⇔
高线
AF 是△ABC的高线⇔∠AFB==90°
中位线
DE 是△ABC的中位线⇔DE∥BC，DE=
注：三角形的中线、中位线、高线都是线段.
-
12、下列每组数分别表示3 根小木棒的长度（单位：cm），其中能搭成三角形的是 （ ）A、3，7，10 B、6，7，8 C、7，7，14 D、5，7，13
-
13、在下列长度的四条线段中，能与长6 cm，8cm 的两条线段围成一个三角形的是（ ）A、1 cm B、2cm C、13 cm D、14 cm
-
14、(1)、三角形任何两边的和④第三边(2)、三角形任何两边的差⑤第三边
-
15、将一副三角板按如图所示方式摆放，使有刻度的边互相垂直，则∠1=（ ）
A、45° B、50° C、60° D、75° -
16、 如图，∠1 的度数为 ， ∠2 的度数为.
-
17、
定理
三角形三个内角的和等于
推论
三角形的外角等于与它的和
-
18、 在△ABC中，若∠A：∠B：∠C=1：3：6，则△ABC的形状是 （ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、形状不确定
-
19、
-
20、 如图，在△ABC中，过点 C作CD⊥AB于点D，G是AC 上任意一点，连结 DG，F 是BC 上任意一点，过点 F 作FE⊥AB 于点 E，且∠1=∠2，∠3=80°.
(1)、求证：∠B=∠ADG；(2)、求∠BCA 的度数.