-
1、如图,下面的四个盒子中,每个盒子里都有两根小棒,把其中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾相接,能够围成一个三角形的是( )A、
 B、
B、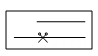 C、
C、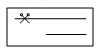 D、
D、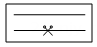
-
2、油纸伞是汉族古老的传统用品之一.图1是一把油纸伞实物图,图2 为其伞骨示意图.已知 那么△AED ≌△AFD 的依据是( )
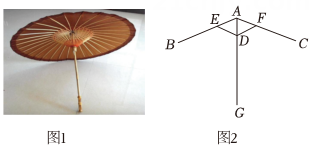 A、SSS B、ASA C、AAS D、SAS
A、SSS B、ASA C、AAS D、SAS -
3、如图,烧杯内液体表面AB 与烧杯下底部CD平行,光线EF 从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.若∠GFH=30°,∠CEF=125°, 则∠HFB 的度数为 ( )
 A、15° B、25° C、45° D、55°
A、15° B、25° C、45° D、55° -
4、数学来源于生活,又服务于生活.以下四幅图中用数学原理解释不正确的是( )
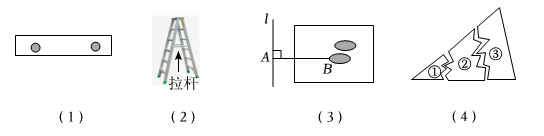 A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS
A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS -
5、设一个正方形的边长为 a cm。若其边长增加了4cm,则新正方形的面积增加了( )A、(8a+16) cm2 B、 C、 D、
-
6、下列事件中,属于必然事件的是( )A、明天的最高气温将达35℃ B、任意购买一张动车票,座位刚好挨着窗口 C、掷两次质地均匀的硬币,其中有一次正面朝上 D、对顶角相等
-
7、对某品种的麦粒在相同条件下进行发芽试验,结果如下表所示:
试验的麦粒数n
200
500
1000
2000
5000
发芽的粒数m
191
473
954
1906
4748
发芽的频率m/n
0.955
0.946
0.954
0.953
0.9496
根据上表,在这批麦粒中任取一粒,估计它能发芽的概率为( )
A、0.92 B、0.95 C、0.97 D、0.98 -
8、综合与探究
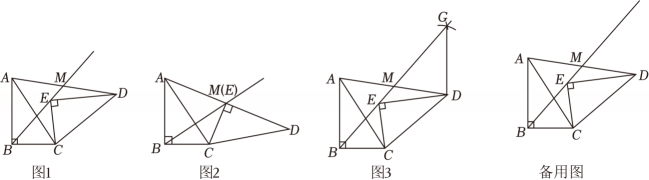
【问题情境】在数学综合实践课上,老师让同学们用两张全等的直角三角形纸片进行摆放,使一锐角顶点重合.如图1,已知△ABC≌△DEC , ∠ABC=∠DEC=90°,连接AD , 射线BE与线段AD交于点M , 并思考点M是否是线段AD的中点;
(1)、【特例探究】勤学小组将它们按照图2的方式摆放,A , E , D三点在同一直线上,此时点E与点M重合,同学们发现点M恰好是线段AD的中点,请你说明理由;(2)、【一般探究】善思小组受勤学小组的启发,发现摆放在一般位置时,点M仍为线段AD的中点,小明写出了他的思路:如图3,以点D为圆心,DE的长为半径作弧交射线BE于点G , 则DG=DE , ……,请你按照小明的思路说明点M是线段AD的中点;(3)、【变式探究】智慧小组继续改变△DEC的位置进行探究,且点E始终在直线BC的上方.若∠BAC=35°,当△ABM是等腰三角形时,请直接写出∠ABM的度数. -
9、
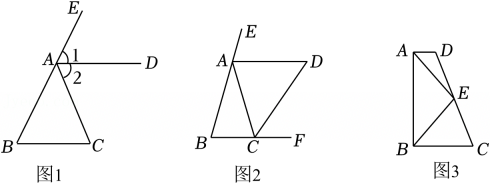 (1)、【基础探究】如图1,AD平分∠EAC , AD∥BC , △ABC是等腰三角形吗?为什么?
(1)、【基础探究】如图1,AD平分∠EAC , AD∥BC , △ABC是等腰三角形吗?为什么?【形成经验】当角平分线遇上平行线时一般会产生等腰三角形.
(2)、【经验应用】如图2,AD∥BC , AD平分∠EAC , CD平分∠ACF , 试探究线段AB与线段AD的数量关系,并说明理由.(3)、【拓展提升】如图3,在四边形ABCD中,AD∥BC , E为CD的中点,且AE平分∠BAD , 请直接写出线段AD、BC和AB之间的数量关系. -
10、如图是由边长为1的小正方形组成的6×6网格,每个小正方形的顶点叫做格点,线段AB的两个端点都在格点上,仅用无刻度的直尺在给定网格中完成画图.
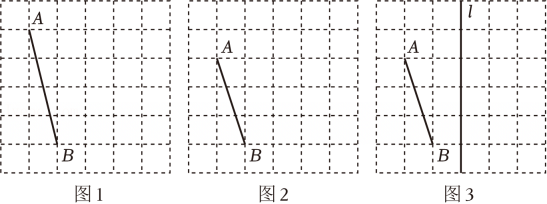 (1)、在图1中以线段AB为边作锐角△ABC(点C在格点上),使其成为轴对称图形(作出一个即可);(2)、在图2中以线段AB为腰作等腰直角△ABC(作出一个即可),△ABC的面积为 ▲ ;(3)、在图3中的直线l上画出点P , 使得PA+PB最短.
(1)、在图1中以线段AB为边作锐角△ABC(点C在格点上),使其成为轴对称图形(作出一个即可);(2)、在图2中以线段AB为腰作等腰直角△ABC(作出一个即可),△ABC的面积为 ▲ ;(3)、在图3中的直线l上画出点P , 使得PA+PB最短. -
11、由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过140km/h),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速v(km/h)
0
10
20
30
40
50
…
刹车距离s(m)
0
2.5
5
7.5
10
12.5
…
请回答下列问题:
(1)、在这个变化过程中,自变量是 ,因变量是 ;(2)、当刹车时车速为60km/h时,刹车距离是 m;(3)、根据上表反映的规律写出该种型号汽车s与v之间的关系式: ;(4)、该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为32m , 推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?(相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时120公里.)
-
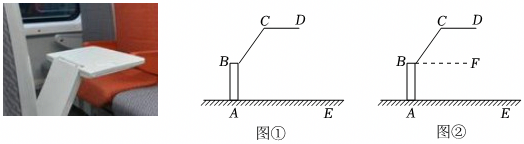
12、高速列车为了方便乘客放置小件物品,在座椅的后方都安装了可折叠的小桌板,将小桌板放下后,桌面与车厢的底部AE平行,从侧面观察得到如图①所示图形,BA⊥AE , 垂足为A , CD∥AE , 有同学认为在这种情况下,∠ABC与∠BCD的和是个定值,下面是小林同学计算∠ABC+∠BCD的度数的过程,请你将解答过程补充完整.
解:如图②,过点B作BF∥AE ,
因为CD∥AE( ),
所以( )∥CD(平行于同一条直线的两条直线平行),
所以∠BCD+∠CBF=( )°( ),
因为AB⊥AE( ),
所以∠EAB=( )°(垂直定义),
因为BF∥AE ,
所以( )+∠EAB=180°,
所以∠ABF=180°﹣90°=( )°,
所以∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=( )°.
-
13、“一人一盔安全守规,一人一戴平安常在”,如表是某厂质检部门对该厂生产的一批头盔质量检测的情况.
抽取的头盔数
500
1000
1500
2000
3000
4000
合格品数
491
986
1470
1964
2949
3932
合格品频率
0.982
0.986
0.980
a
b
0.983
(1)、求出表中a= ,b= ;(2)、从这批头盔中任意抽取一顶是合格品的概率的估计值是 (精确到0.01);(3)、如果要出厂49000顶合格的头盔,则该厂估计要生产多少顶头盔? -
14、如图,点C处有一灯塔,一艘轮船从点A开始按箭头所示方向行驶,当行驶到点B时,轮船到灯塔的距离恰好等于行驶的距离.
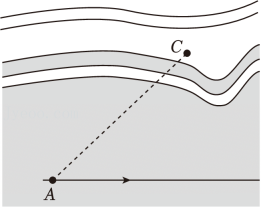 (1)、请用尺规在图中画出点B的位置;(2)、若∠CAB=42°,则∠ABC= °.
(1)、请用尺规在图中画出点B的位置;(2)、若∠CAB=42°,则∠ABC= °. -
15、在学习综合与实践《设计自己的运算程序》时,小明设计了一个如下运算程序:任意写出一个三位数(三位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差.重复这个过程…若以365开始,按照此程序运算2025次后得到的数是 .
-
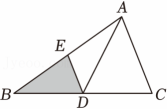
16、如图,AD是△ABC中BC边的中线,点E是AB的中点,连接DE、AD , 现随机向△ABC内掷一枚小针,则针尖落在阴影区域的概率是 .
-
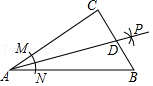
17、如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC , AB于点M、N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P , 作射线AP交边BC于点D , 若CD=3,AB=10,则△ABD的面积是 .
-
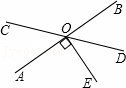
18、如图,直线AB、CD相交于点O , OE⊥AB , 垂足是点O , ∠BOC=140°,则∠DOE= .
-
19、计算 .
-
20、“一把剪刀蕴神技,一方红纸酿年味”,剪纸是中国传统的民间艺术,是中国的非物质文化遗产,随着社会的发展形成了一定特征的数学文化.如图,小明在剪纸活动中,将一张长方形纸片对折三次后,沿着虚线剪去一个角,再打开后的形状是( )
 A、
A、 B、
B、 C、
C、 D、
D、