-
1、如图，小明同学拿着老师的等腰直角三角尺，摆放在两摞长方体教具之间，∠ACB=90°，AC=CB，每个小长方体教具高度均为4 cm.
(1)、求证：△ACD≌△CBE.(2)、求DE的长. -
2、如图所示，已知线段a及∠α，求作△ABC，使AB=a，AC=2a，∠A=2∠α，写出作法，保留作图痕迹.
-
3、如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F.如果AB=10，AE=3，求线段CF的长度.
-
4、如图，AB=AD，∠BAC=∠DAC=25°，∠D=80°.求∠BCA的度数.
-
5、如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，已知EH=EB=4，S△AEH=12，则CH的长为.
-
6、如图，点B，E，C，F在同一直线上，△ABC≌△DEF，AC，DE交于点M.若∠B=50°，∠F=60°，则∠AMD的度数为.
-
7、如图，在△ABC中，点D在AB上，点E在BC上，且BD=BE，请你再添加一个条件，使得△BEA≌△BDC，你添加的条件是.(只需添加一个正确的即可)
-
8、如图，已知线段AB=18，MA⊥AB于点A，MA=6，射线BD⊥AB于点B，点P从点B向点A运动，每秒走1个单位长度，点Q从点B向点D运动，每秒走2个单位长度，点P，Q同时从点B出发，若出发x s后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为( )
A、4 B、6 C、4或9 D、6或9 -
9、如图，在四边形ABCD中，AB∥CD，∠1=∠2，AD=CE.若AB=2，BE=3，则CD的长为( )
A、4 B、5 C、6 D、7 -
10、如图是一个正方形网格，每个小正方形的边长相等，我们把该网格中正方形的顶点称之为“好点”，△ABC的三个顶点都在这个正方形网格的“好点”上，在这个正方形网格图中找一个“好点”D(点D与点A不重合)，使得以点D，B，C为顶点的三角形与△ABC全等，则这样的“好点”D的个数为( )
A、1 B、2 C、3 D、4 -
11、如图，已知点B，C，E在同一条直线上，∠B=∠E=∠ACD=60°，AB=CE，则图中与BC相等的线段是( )
A、AC B、DE C、DC D、AD -
12、如图，在△ABC和△DEF中，点B，C，E，F在同一条直线上，AB=DE，AC=DF，BE=CF，∠A=95°，∠DEF=15°，则∠F的度数为( )
A、25° B、60° C、70° D、95° -
13、如图，一块三角形的玻璃打碎成四块，现要到玻璃店去配一块与原来完全一样的玻璃，最简单的办法是( )
A、只带①去 B、带②③去 C、带①③去 D、只带④去 -
14、如图，△ABC≌△A'BC'，过点C作CD⊥BC'，垂足为D，若∠ABA'=55°，则∠BCD的度数为( )
A、25° B、35° C、45° D、55° -
15、下列命题的逆命题是真命题的是( )A、钝角三角形中有两个锐角 B、若a2=b2 ， 则a=b C、钝角大于90° D、若a<b，则ac<bc
-
16、如图，直棱柱的底面边长都相等，底面边长是3.5cm，高是4cm，解答下列问题．
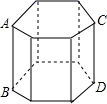(1)、这是几棱柱，共有几个面？(2)、这个棱柱的侧面积是多少cm2？ -
17、一个直角三角形的三条边长分别是3cm、4cm、5cm，若以斜边5cm为轴旋转一周形成的图形体积是立方厘米．（π取3.14）
-
18、若关于x 的一元二次方程ax2＋2x－＝0（a＜0）有两个不相等的实数根，则a的取值范围是（ ）A、a＜－2 B、a＞－2 C、－2＜a＜0 D、－2≤a＜0
-
19、已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE，且CA＝CD，CB＝CE，∠ACD＝∠BCE，直线AE与BD交于点F，
(1)、如图①，若∠ACD＝60°，则∠AFB＝ ；如图②，若∠ACD＝90°，则∠AFB＝ ；如图③，若∠ACD＝120°，则∠AFB＝ ；(2)、如图④，若∠ACD＝α，则∠AFB＝ （用含α的式子表示）；(3)、将图④中的△ACD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），变成如图⑤所示的情形，若∠ACD＝α，则∠AFB与α的有何数量关系？并给予证明． -
20、如图，△ABC中，AC的垂直平分线交AC于点F，交BC于点E，AD⊥BC且BD＝DE，连接AE．
(1)、求证：AB＝EC；(2)、若△ABC的周长为28cm，AC＝12cm，求DC长．